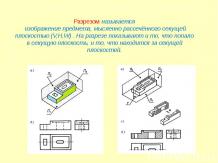
Презентация на тему: Аксиомы стереометрии. Следствия из аксиом

Аксиомы стереометрии. Следствия из аксиом Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины ИвановныПреподавателя ГБОУ НПО ПЛ №80.

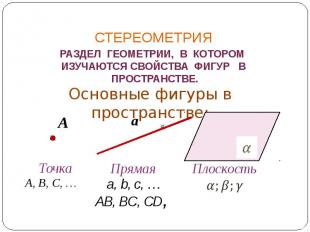
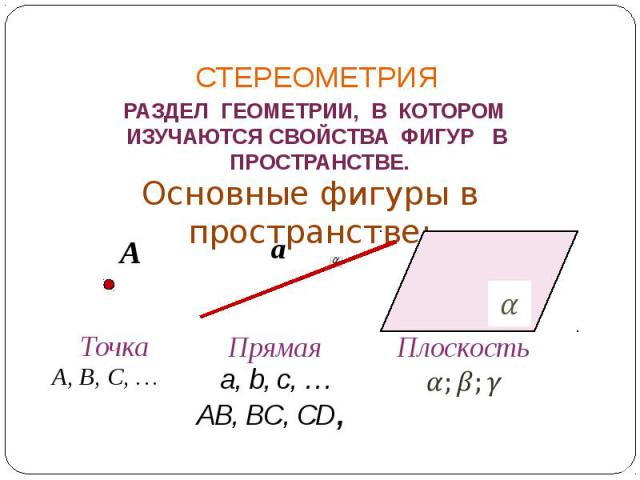
СТЕРЕОМЕТРИЯ РАЗДЕЛ ГЕОМЕТРИИ, В КОТОРОМ ИЗУЧАЮТСЯ СВОЙСТВА ФИГУР В ПРОСТРАНСТВЕ. Основные фигуры в пространстве: Точка A, B, C, … Прямая AВ, BС, CD, Плоскость

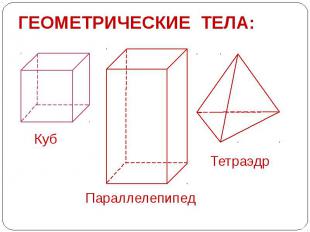
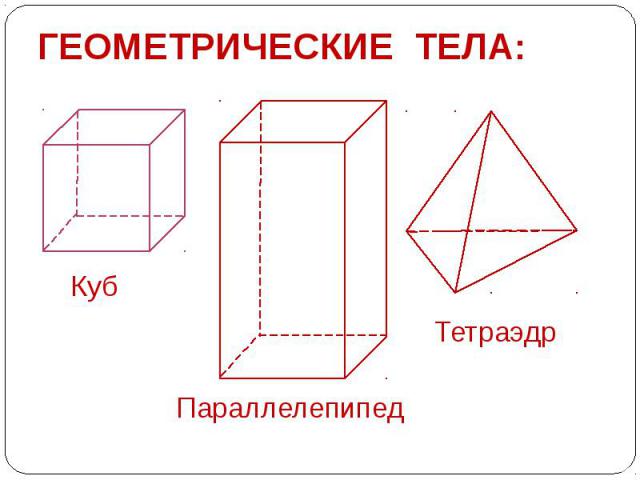
ГЕОМЕТРИЧЕСКИЕ ТЕЛА:

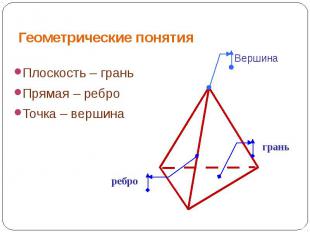
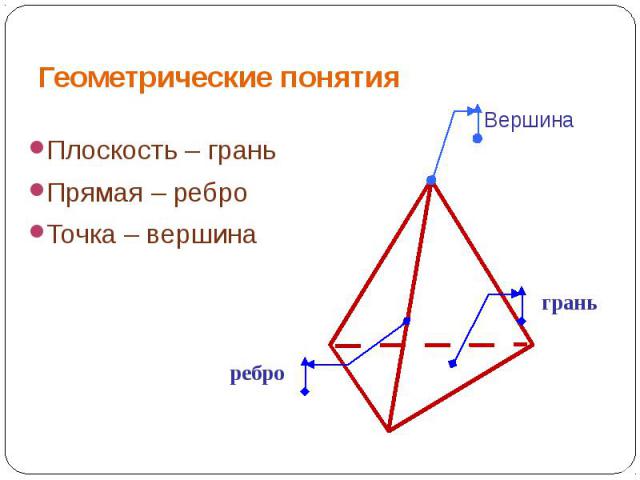
Геометрические понятия Плоскость – граньПрямая – реброТочка – вершина

Аксиома(от греческого axíõma – принятие положения) Исходное положение научной теории, принимаемое без доказательства.

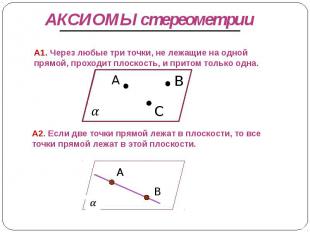
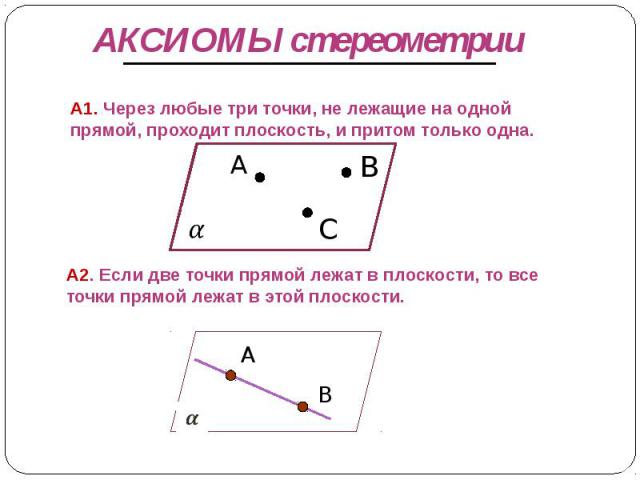
АКСИОМЫ стереометрии А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

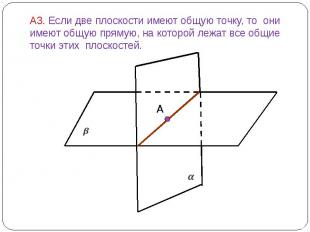
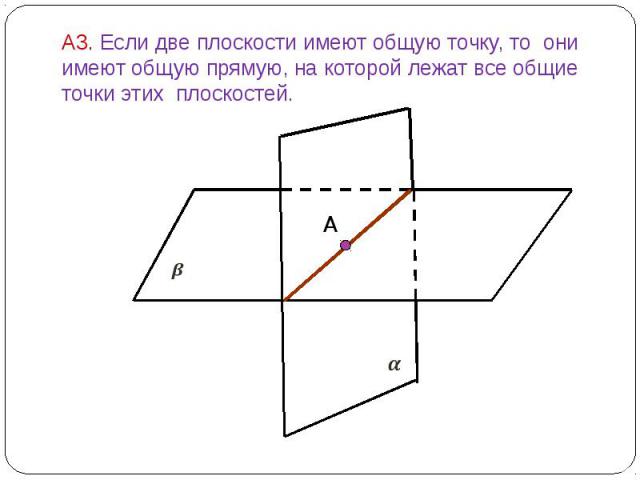
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

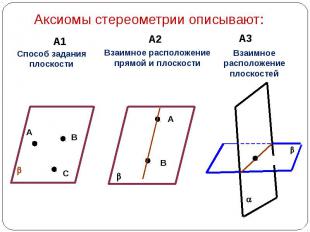
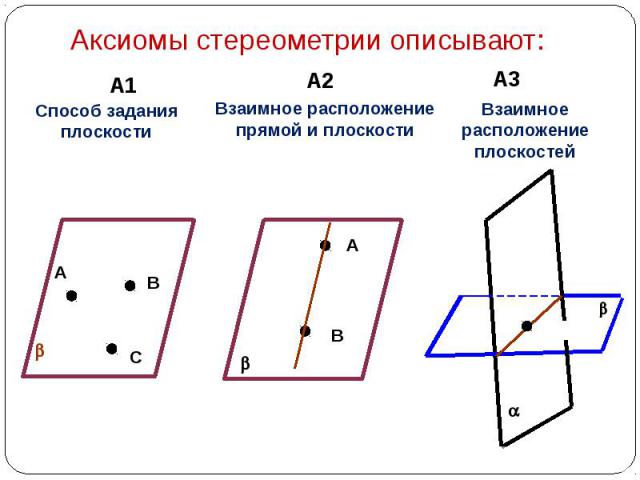
Аксиомы стереометрии описывают: Способ задания плоскости Взаимное расположение прямой и плоскости Взаимное расположение плоскостей

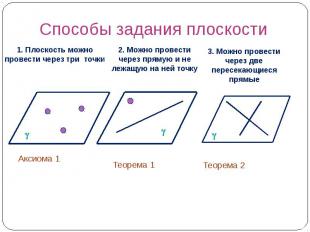
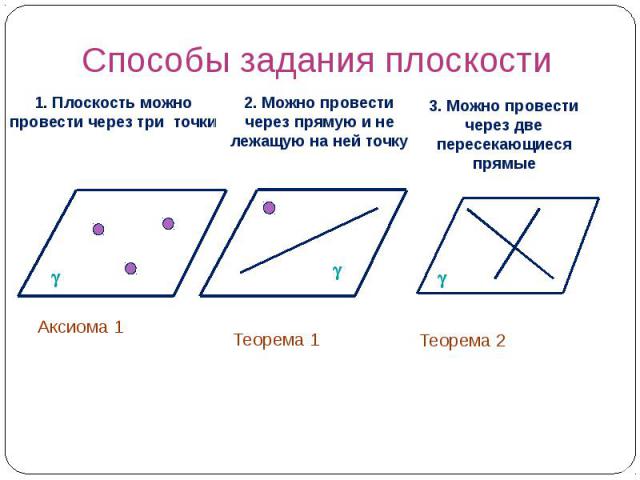
Способы задания плоскости 1. Плоскость можно провести через три точки 2. Можно провести через прямую и не лежащую на ней точку 3. Можно провести через две пересекающиеся прямые

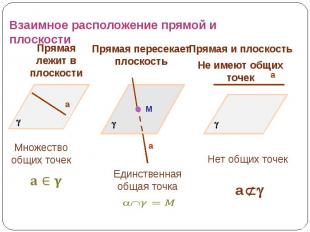
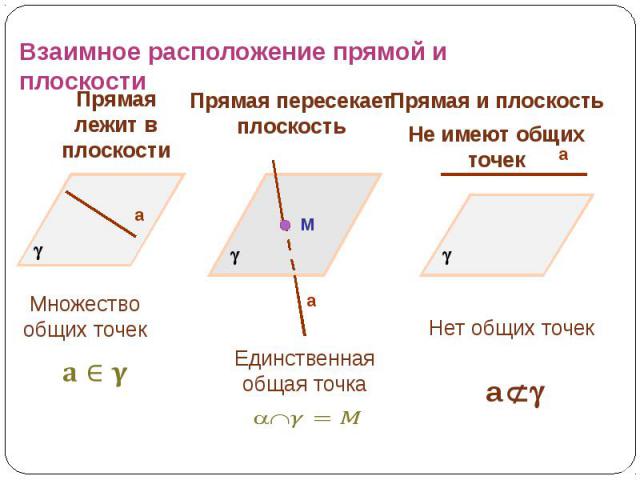
Взаимное расположение прямой и плоскости Прямая лежит в плоскости Прямая пересекает плоскость Прямая и плоскостьНе имеют общих точек Множество общих точек Единственная общая точка Нет общих точек

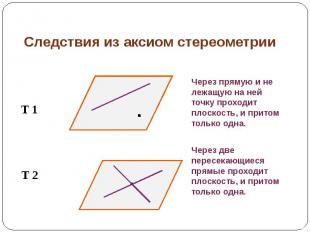
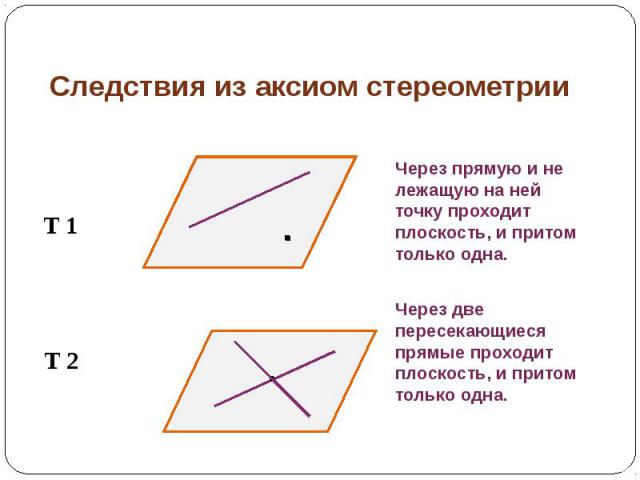
Следствия из аксиом стереометрии

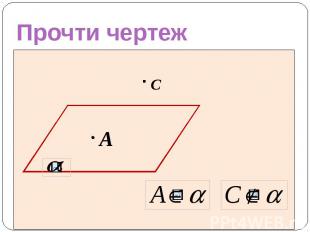
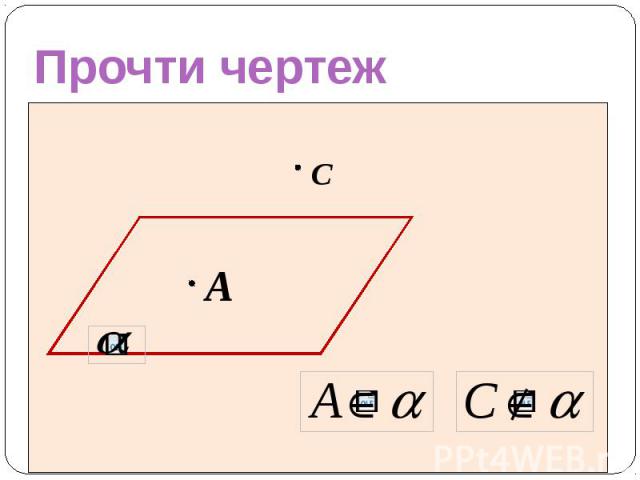
Прочти чертеж

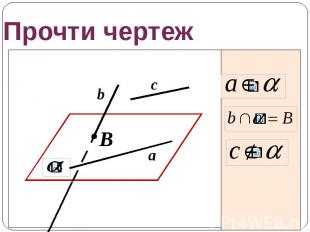
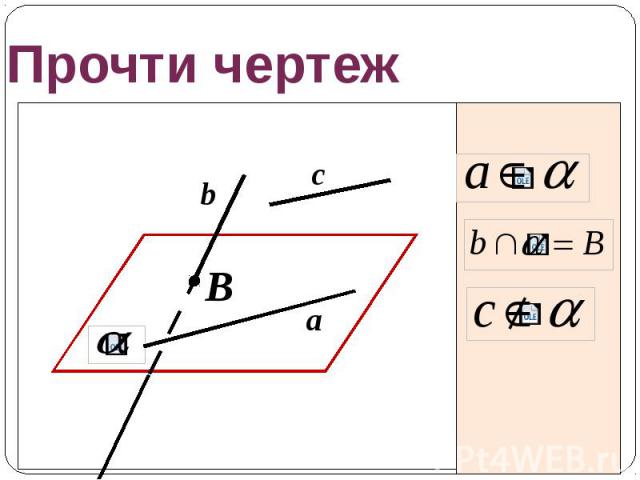
Прочти чертеж

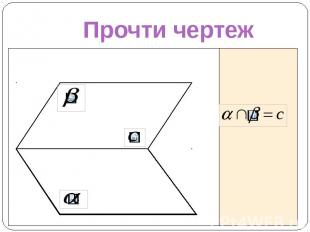
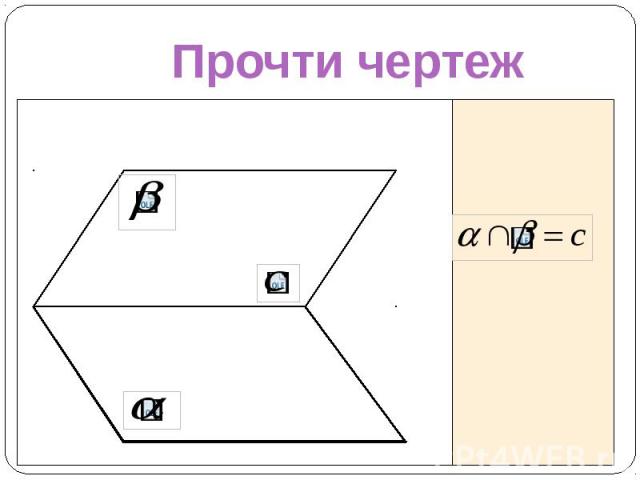
Прочти чертеж

Самостоятельная работа