Презентация на тему: Геометрические преобразования и паркеты

Геометрические преобразования и паркеты

«Математика владеет не только истиной, но и высшей красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства». Бертран Рассел.

Цель проектаДанный проект поможет повысить интерес учащихся к математике. В теме проекта кроется возможность показать умение видеть, наблюдать, анализировать, выделять главное, обобщать увиденное и связывать наблюдения с сутью явлений в природе. Конечная цель- умение на основе математических моделей решать проблемы социальные, технологические, экономические, научные, умение работать с новыми информационными технологиями.

Геометрические паркеты Паркет (или мозаика) - бесконечное семейство многоугольников, покрывающее плоскость без просветов и двойных покрытий. Иногда паркетом называют покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек; но мы будем рассматривать как правильные, так и неправильные многоугольники.Итак, какими же многоугольниками можно замостить плоскость?

Паркеты из одинаковых правильных многоугольников. Можно получить паркеты, составленные из правильных треугольников, квадратов или правильных шестиугольников.

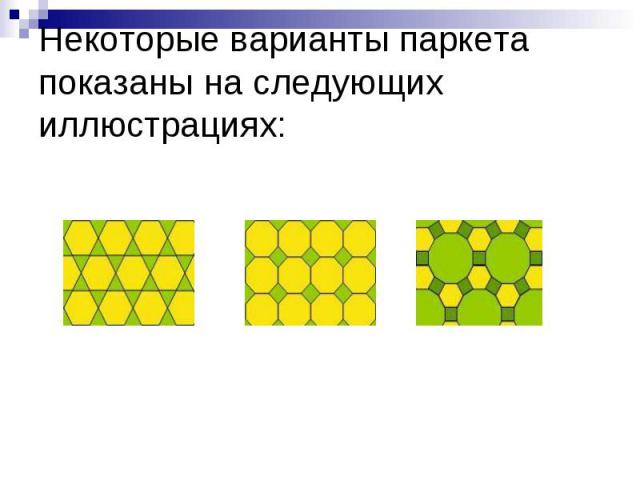
Паркеты из разных правильных многоугольников.Существуют следующие способы уложить паркет комбинациями правильных многоугольников: (3,12,12); (4,6,12); (6,6,6); (3,3,6,6) - два варианта паркета; (3,4,4,6) - четыре варианта; (3,3,3,4,4) - четыре варианта; (3,3,3,3,6); (3,3,3,3,3,3) (цифры в скобках - обозначения многоугольников, сходящихся в каждой вершине: 3 - правильный треугольник, 4 - квадрат, 6 - правильный шестиугольник, 12 - правильный двенадцатиугольник).

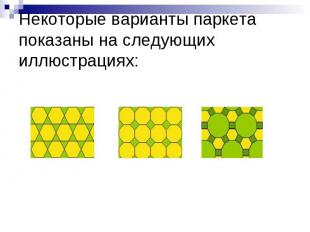
Некоторые варианты паркета показаны на следующих иллюстрациях:

Паркеты из неправильных многоугольников. Легко покрыть плоскость параллелограммами: Вообще можно замостить плоскость копиями произвольного четырехугольника, необязательно выпуклого:

Можно составить паркет из копий произвольного треугольника: из двух равных треугольников можно сложить параллелограмм, и покрыть плоскость копиями этого параллелограмма.

Паркеты из невыпуклых семиугольников

Паркеты из произвольных фигур.Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом называется покрытие плоскости без пропусков и перекрытий заданными фигурами (в частном случае - многоугольниками, правильными или неправильными, выпуклыми или невыпуклыми).

Паркеты, полученные заменой отрезков "квадратной" сетки некоторыми кривыми или ломаными.

Паркеты, полученные в результате объединения элементов квадратной сетки

Паркет, каждый элемент которого получен в результате объединения пяти правильных треугольников

Разбиения сетки из греческих крестов

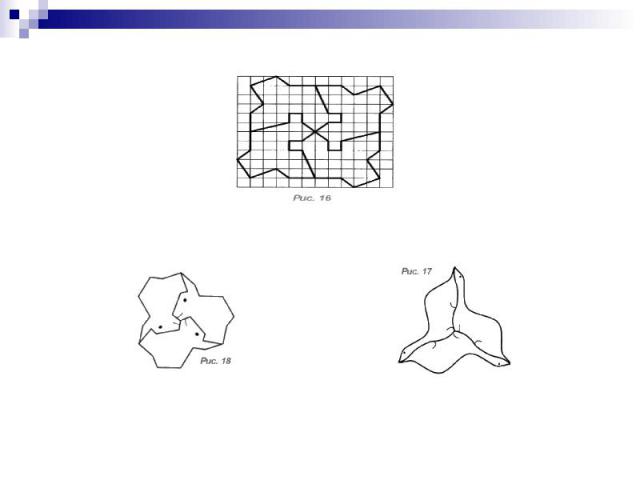
Паркеты, полученные с помощью параллельного переноса

Паркеты Мориса Эшера

Плитки Пенроуза .

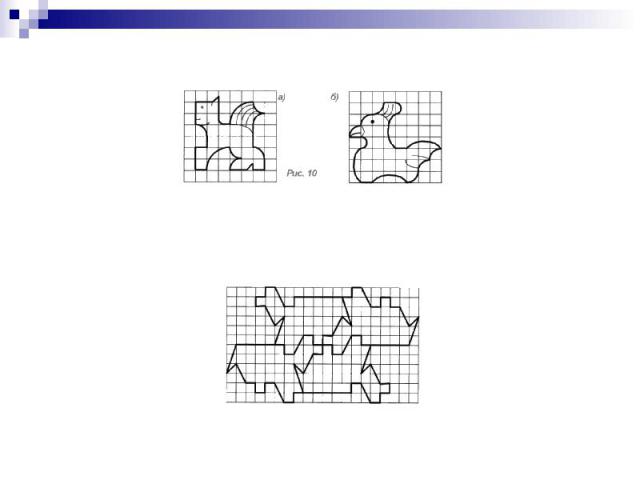
Практическая часть.Простейшим видом паркета является такой, в котором плоскость заполняется фигурами с помощью параллельного переноса и поворота.

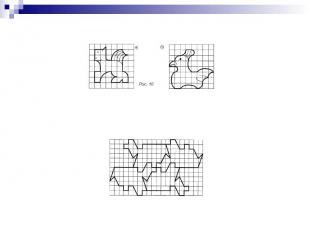
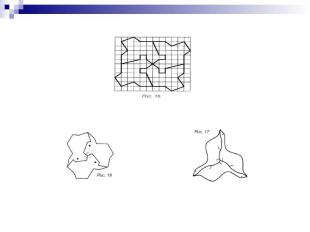
Каждой из фигурок заполните плоскость, получив паркет.

Сравните фигурки. Скопируйте их на кальку и заполните плоскость, получив паркет.

Выполнил ученик 9 класса МОУ «Подгорненская сош» Невзоров Анатолий