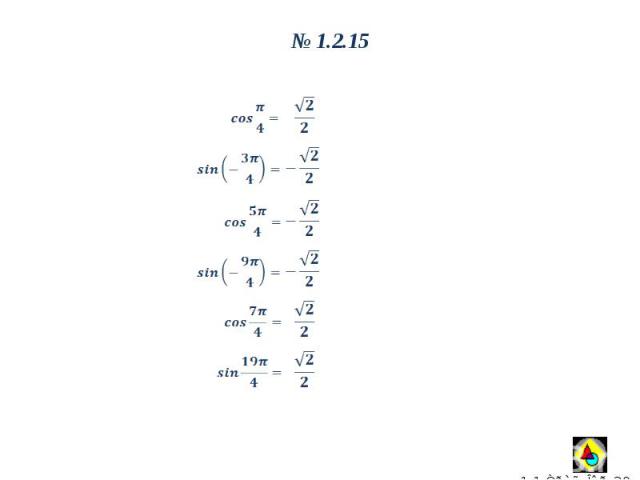Презентация на тему: Радианная мера угла

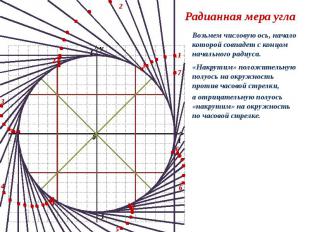
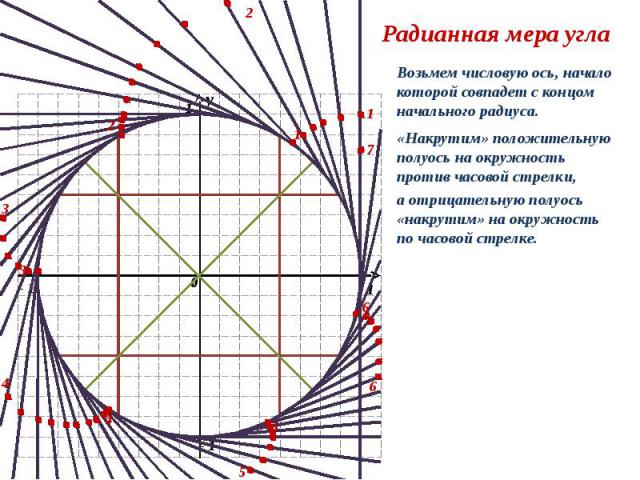
y 0 1 1 - 1 y 0 1 1 2 2 3 3 4 4 5 5 6 6 7 Радианная мера угла Возьмем числовую ось, начало которой совпадет с концом начального радиуса. «Накрутим» положительную полуось на окружность против часовой стрелки, а отрицательную полуось «накрутим» на окружность по часовой стрелке.

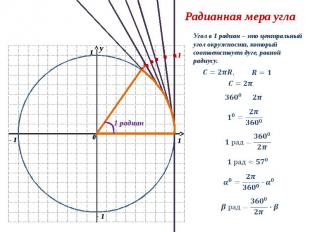
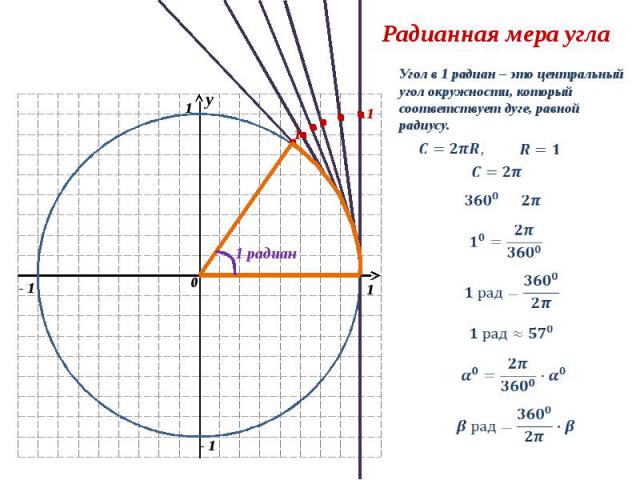
y 0 1 1 - 1 1 1 Радианная мера угла 1 радиан Угол в 1 радиан – это центральный угол окружности, который соответствует дуге, равной радиусу.

1.2.1

1.2.2

1.2.3

1.2.4

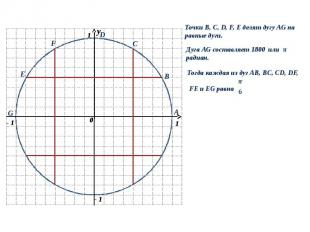
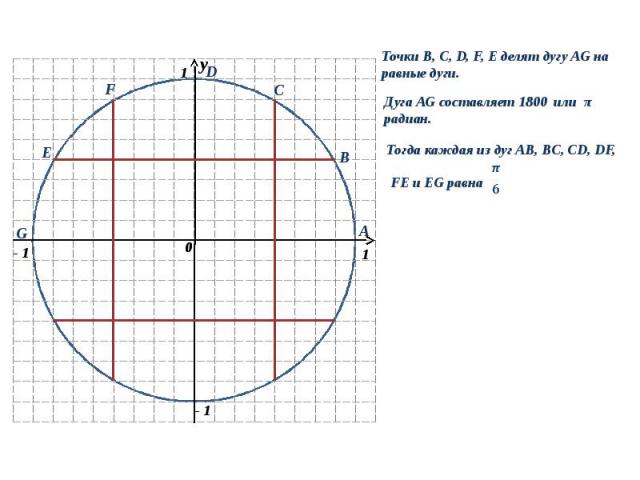
y 0 1 1 - 1 y 0 B A С D F E G Точки B, C, D, F, E делят дугу AG на равные дуги. Дуга AG составляет 180 0 или π радиан. Тогда каждая из дуг AB, BC, CD, DF, FE и EG равна

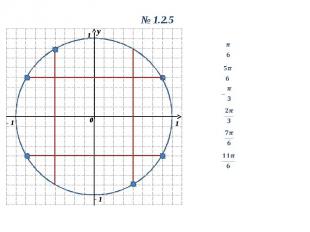
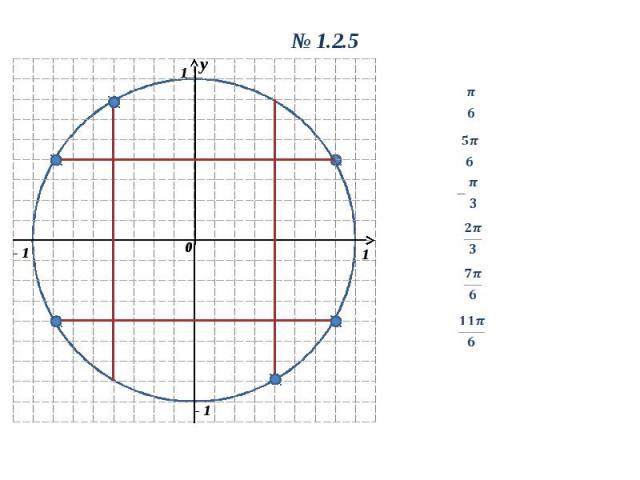
y 0 1 1 - 1 y 0 1.2.5

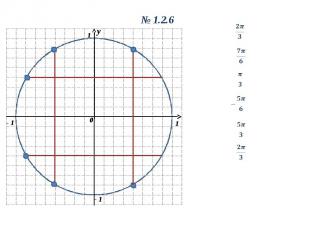
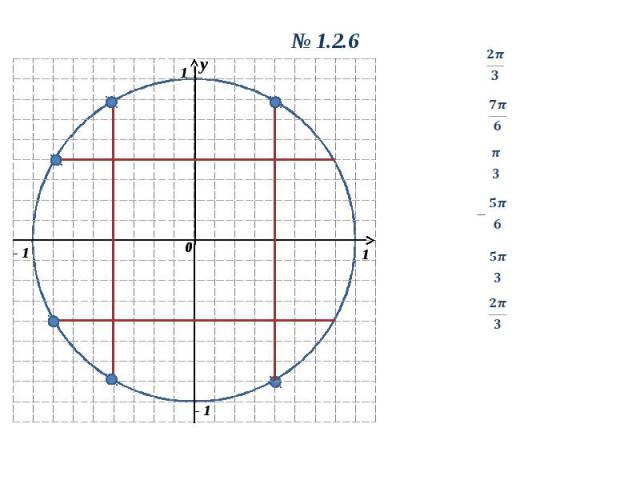
y 0 1 1 - 1 y 0 1.2.6

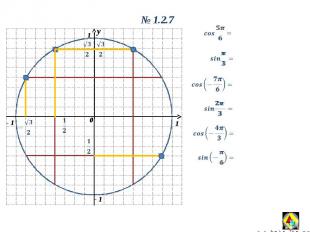
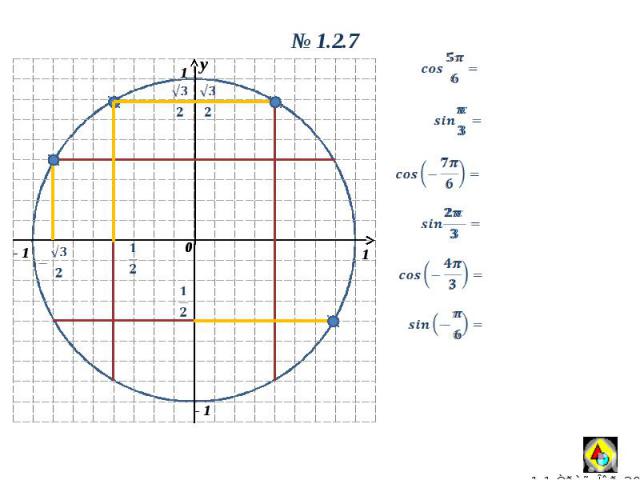
y 0 1 1 - 1 y 0 1.2.7

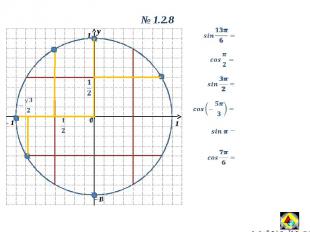
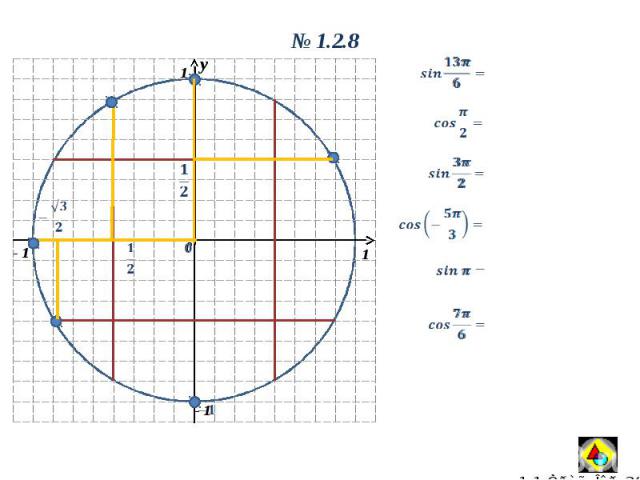
y 0 1 1 - 1 y 0 1.2.8

1.2.9

1.2.10

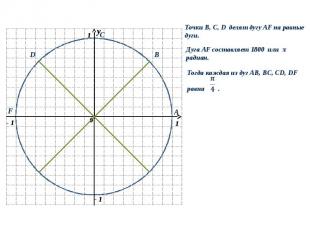
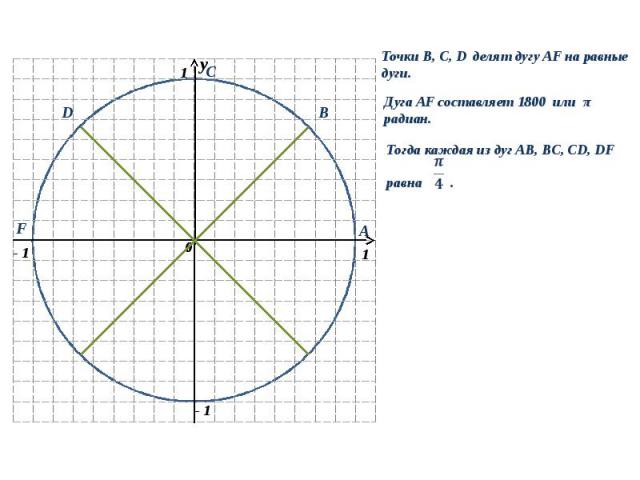
Точки B, C, D делят дугу AF на равные дуги. Дуга AF составляет 180 0 или π радиан. Тогда каждая из дуг AB, BC, CD, DF равна. y 0 1 1 - 1 y 0 B A С D F

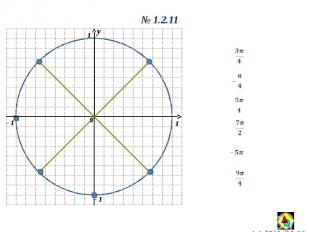
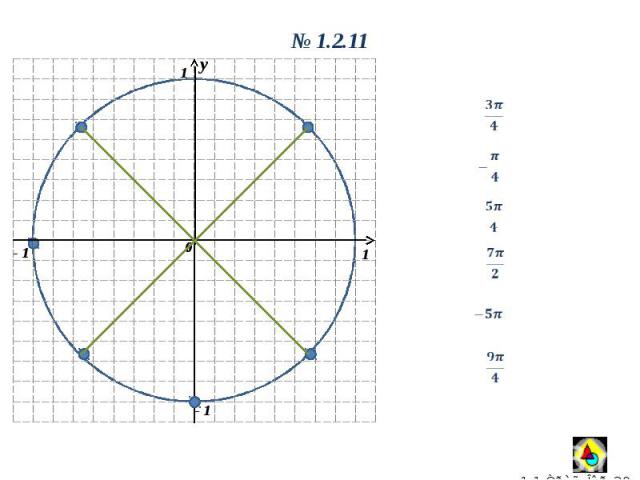
y 0 1 1 y 0 1.2.11

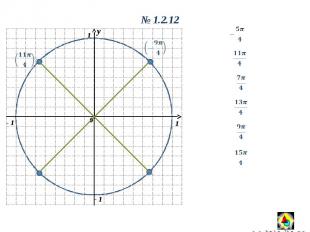
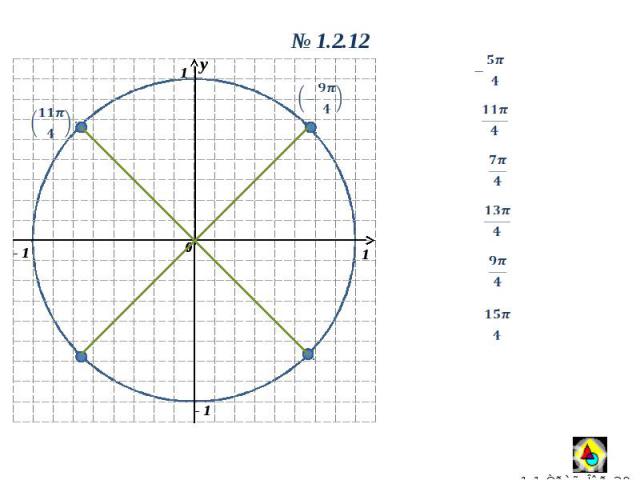
y 0 1 1 y 0 1.2.12

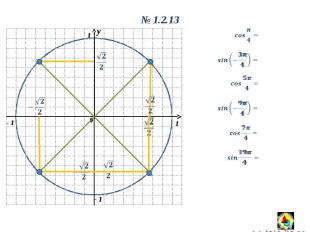
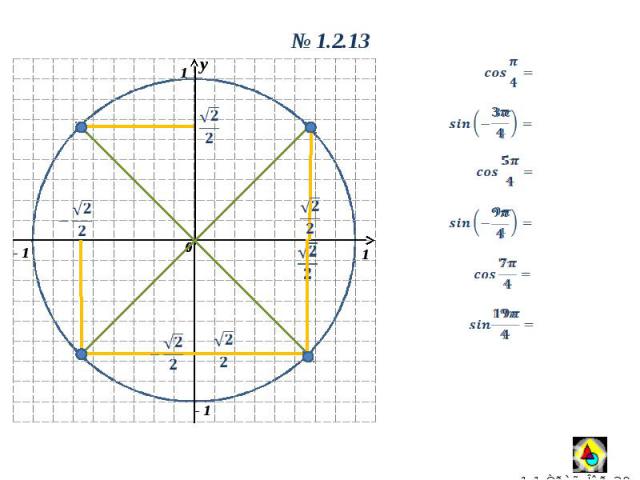
y 0 1 1 y 0 1.2.13

1.2.14

1.2.15

1.2.16

1.2.17

1.2.18

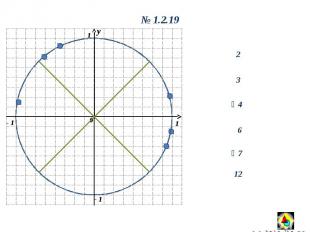
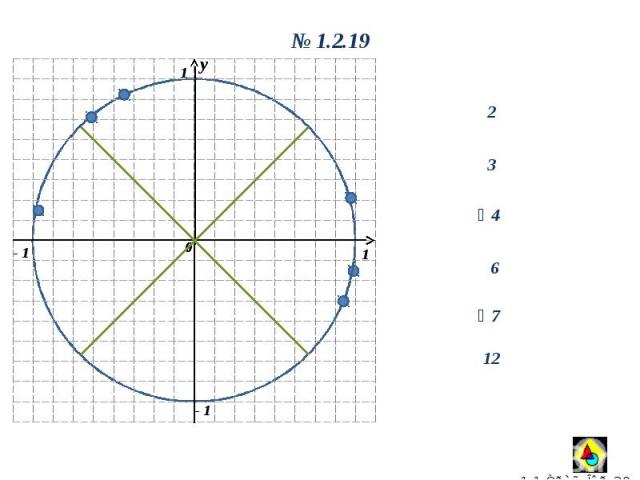
y 0 1 1 - 1 y 0 1.2.19 2 3 4 7 6 12

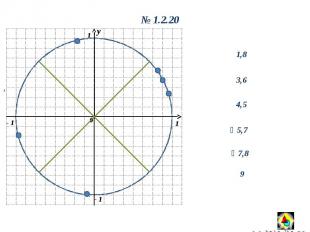
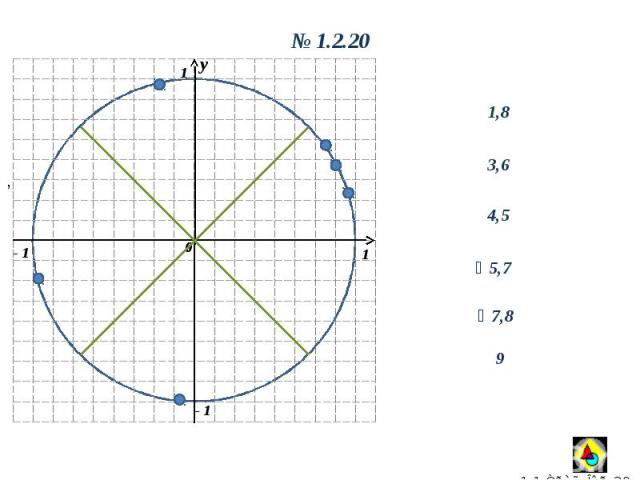
y 0 1 1 - 1 y 0 1.2.20, 1,8 3,6 4,5 7,8 5,7 9

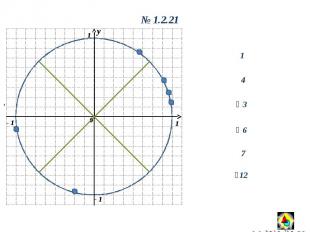
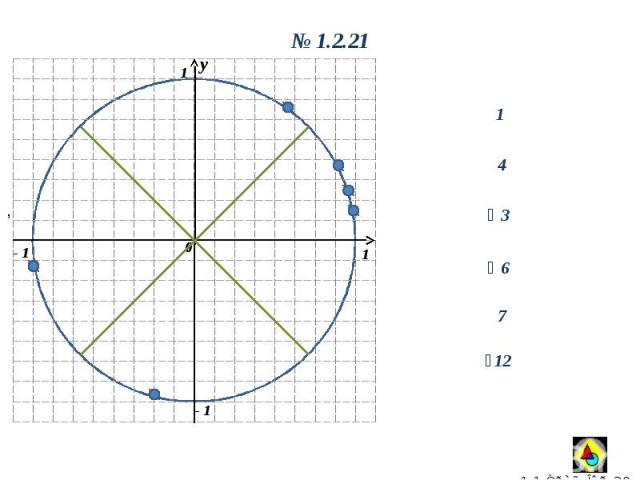
, y 0 1 1 - 1 y 0 1.2.21 1 4 3 7 6 12

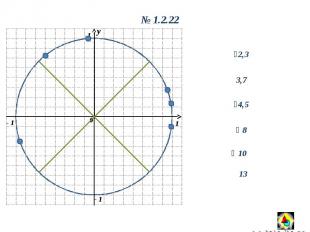
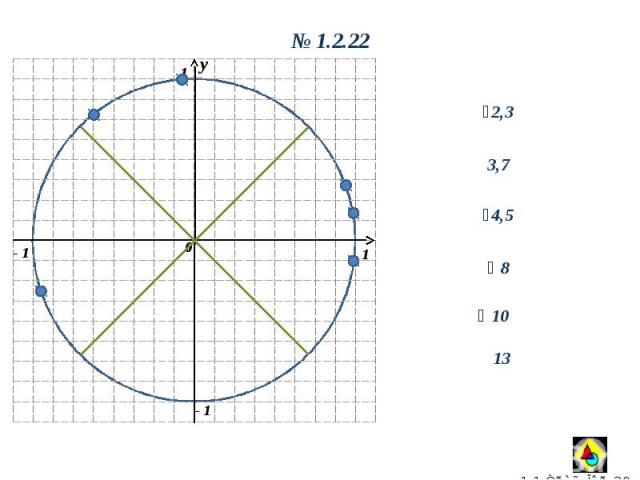
y 0 1 1 - 1 y 0 1.2.22 2,3 3,7 4,5 10 8 13

1,9 IV четверти 1.2.23 3,8 5 17 1,3 2,8 II четверти IV четверти III четверти

5,4 III четверти IV четверти 1.2.24 2,8 3,4 9 16 10 I четверти II четверти I четверти IV четверти