Презентация на тему: Сфера, вписанная в многогранник

Сфера, вписанная в многогранник

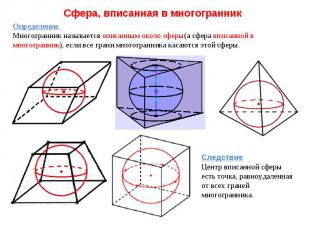
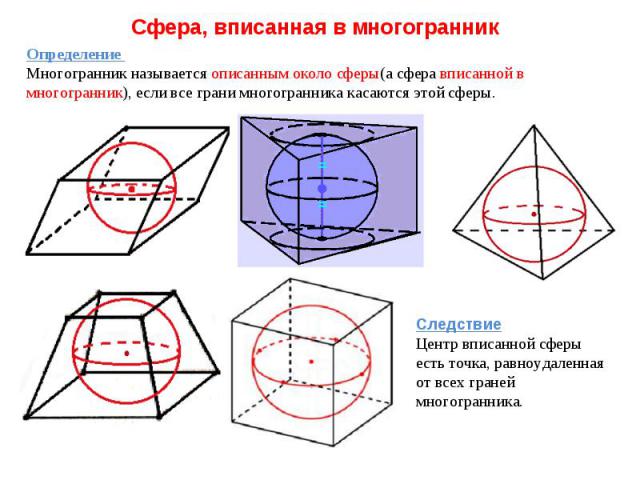
Сфера, вписанная в многогранник Определение Многогранник называется описанным около сферы(а сфера вписанной в многогранник), если все грани многогранника касаются этой сферы. Следствие Центр вписанной сферы есть точка, равноудаленная от всех граней многогранника.

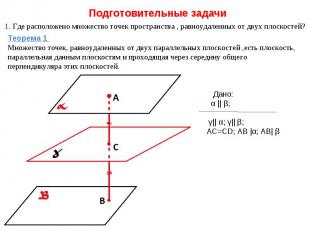
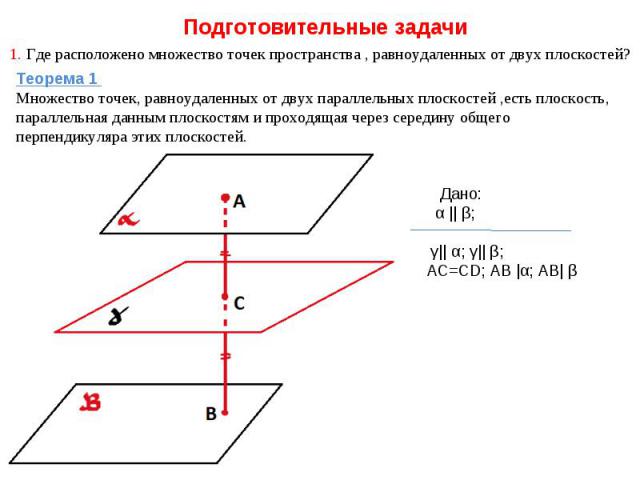
Подготовительные задачи 1. Где расположено множество точек пространства , равноудаленных от двух плоскостей? Теорема 1 Множество точек, равноудаленных от двух параллельных плоскостей ,есть плоскость, параллельная данным плоскостям и проходящая через середину общего перпендикуляра этих плоскостей. Дано: α || β; γ|| α; γ|| β; AC=CD; AB |α; AB| β

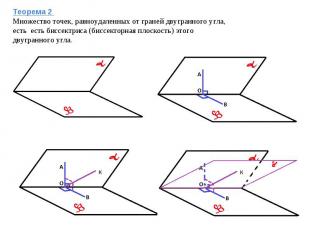
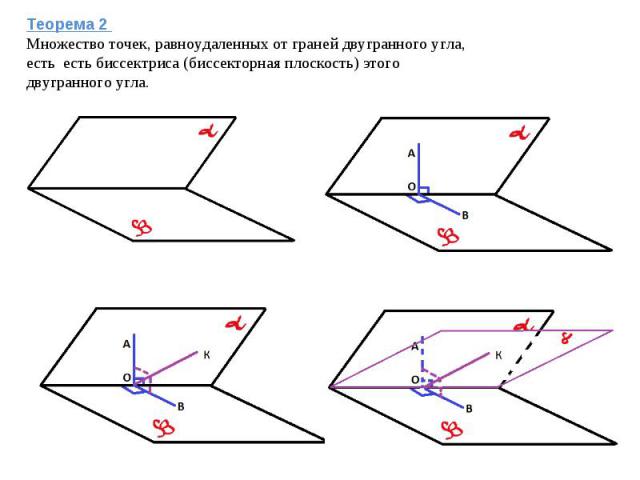
Теорема 2 Множество точек, равноудаленных от граней двугранного угла, есть есть биссектриса (биссекторная плоскость) этого двугранного угла.

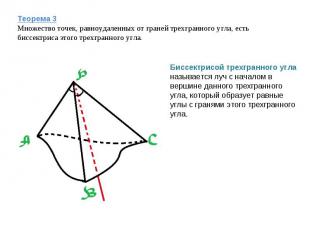
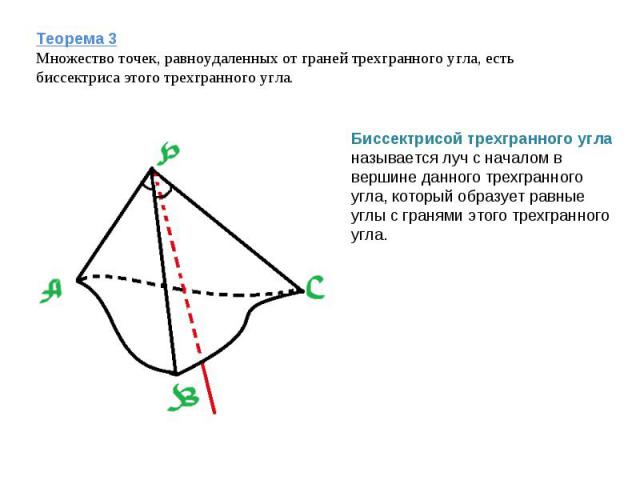
Теорема 3Множество точек, равноудаленных от граней трехгранного угла, есть биссектриса этого трехгранного угла. Биссектрисой трехгранного угла называется луч с началом в вершине данного трехгранного угла, который образует равные углы с гранями этого трехгранного угла.

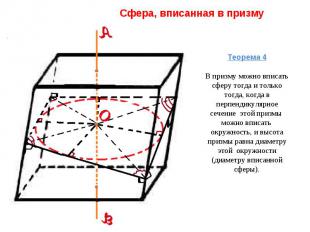
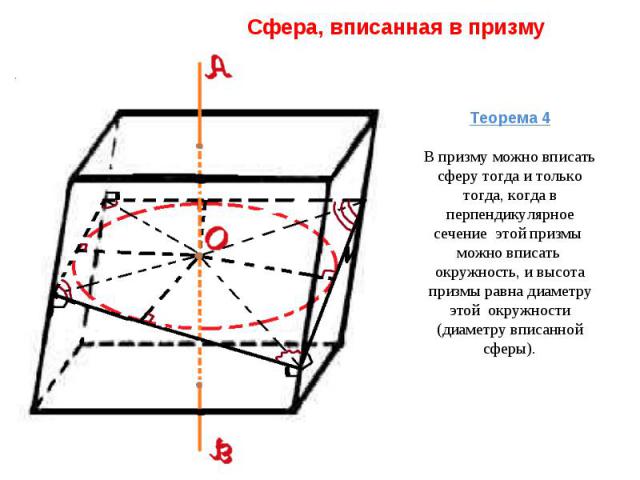
Сфера, вписанная в призму Теорема 4В призму можно вписать сферу тогда и только тогда, когда в перпендикулярное сечение этой призмы можно вписать окружность, и высота призмы равна диаметру этой окружности (диаметру вписанной сферы).

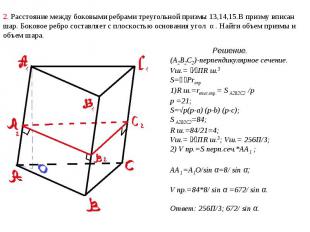
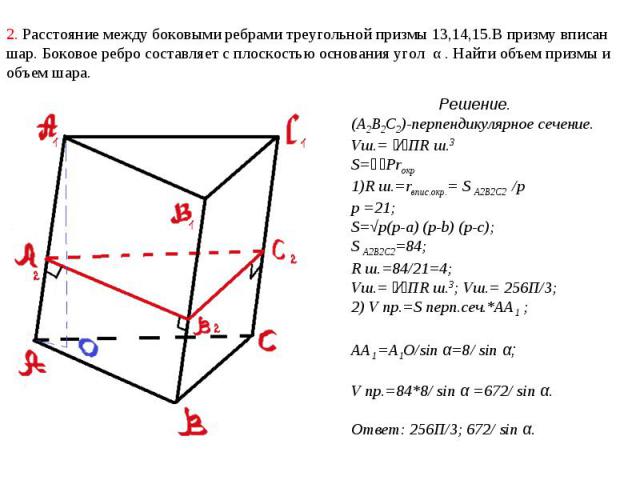
2. Расстояние между боковыми ребрами треугольной призмы 13,14,15.В призму вписан шар. Боковое ребро составляет с плоскостью основания угол α . Найти объем призмы и объем шара. Решение.(А2В2С2)-перпендикулярное сечение. Vш.= ⁴⁄₃ПR ш.3S=⅟₂PrокрR ш.=rвпис.окр.= S А2В2С2 /pp =21;S=√p(p-a) (p-b) (p-c);S А2В2С2=84;R ш.=84/21=4;Vш.= ⁴⁄₃ПR ш.3; Vш.= 256П/3;2) V пр.=S перп.сеч.*АА1 ;АА1 =А1О/sin α=8/ sin α;V пр.=84*8/ sin α =672/ sin α.Ответ: 256П/3; 672/ sin α.

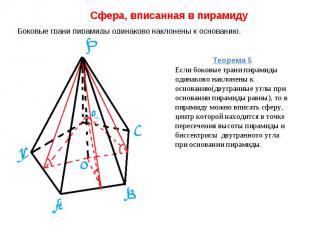
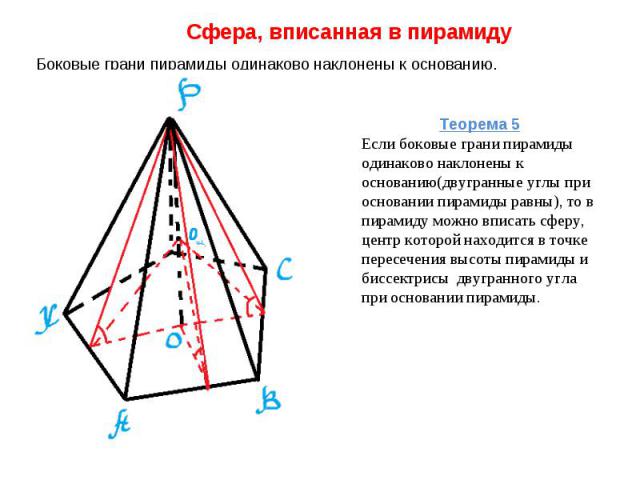
Сфера, вписанная в пирамиду Боковые грани пирамиды одинаково наклонены к основанию. Теорема 5Если боковые грани пирамиды одинаково наклонены к основанию(двугранные углы при основании пирамиды равны), то в пирамиду можно вписать сферу, центр которой находится в точке пересечения высоты пирамиды и биссектрисы двугранного угла при основании пирамиды.

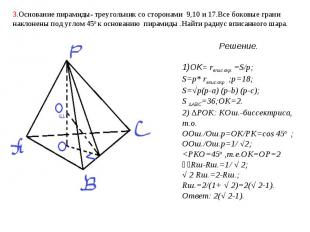
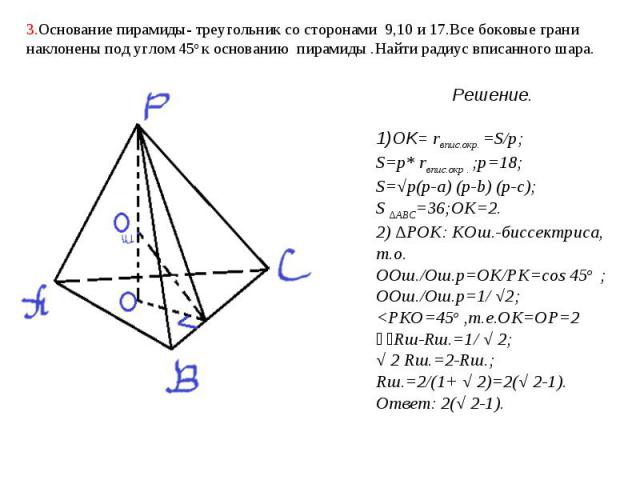
3.Основание пирамиды- треугольник со сторонами 9,10 и 17.Все боковые грани наклонены под углом 45о к основанию пирамиды .Найти радиус вписанного шара. Решение.1)OK= rвпис.окр. =S/p;S=p* rвпис.окр . ;p=18;S=√p(p-a) (p-b) (p-c);S ∆АВС=36;OK=2.2) ∆POK: KOш.-биссектриса, т.о.ООш./Ош.p=OK/PK=cos 45о ;ООш./Ош.p=1/ √2;

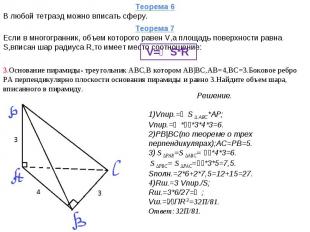
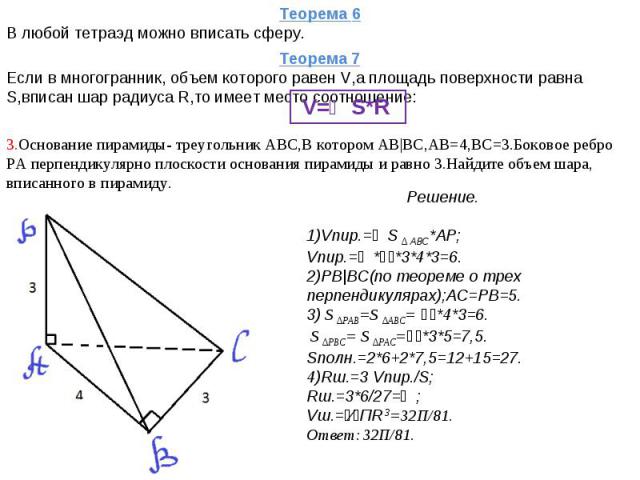
Теорема 6В любой тетраэд можно вписать сферу. Теорема 7Если в многогранник, объем которого равен V,а площадь поверхности равна S,вписан шар радиуса R,то имеет место соотношение: V=⅓S*R 3.Основание пирамиды- треугольник АВС,В котором АВ|ВС,АВ=4,ВС=3.Боковое ребро РА перпендикулярно плоскости основания пирамиды и равно 3.Найдите объем шара, вписанного в пирамиду. Решение.1)Vпир.=⅓S ∆ ABC*AP;Vпир.=⅓*⅟₂*3*4*3=6.2)PB|BC(по теореме о трех перпендикулярах);АС=PB=5.3) S ∆PАВ=S ∆АВС= ⅟₂*4*3=6. S ∆PВC= S ∆PАC=⅟₂*3*5=7,5.Sполн.=2*6+2*7,5=12+15=27.4)Rш.=3 Vпир./S;Rш.=3*6/27=⅔;Vш.=⁴⁄₃ПR 3=32П/81.Ответ: 32П/81.

4. Шар вписан в прямую призму, основание которой- равнобедренная трапеция с основаниями 2 и 8.Найдите объем шара и объем призмы. Решение.1)Rш.= rвпис.окр . ;Hпр.=D впис.окр.=CK.2)DC+AB=AD+CB;2BC=2+8; BC=5.3)BC=⅟₂(AB-DC); BK= ⅟₂(8-2)=3;4) ∆BCK:CK=4; Rш.=2.5)Vпр.=Sосн.*Нпр.;Vпр.=80;Vш.= ⁴⁄₃ПR 3 ;Vш.= ⁴⁄₃П2 3 =32П/3.Ответ: 32П/3.

Спасибо за внимание