Презентация на тему: Равнобедренный треугольник 7 класс

Равнобедренный треугольник Геометрия 7 класс Яковлева Любовь ВикторовнаМБОУ «Самосдельская СОШ им. Шитова В. А.»

Цель урока: ввести определение равнобедренного треугольника и его элементов; познакомится со свойством углов равнобедренного треугольника;научиться пользоваться доказанным свойством при решении задач.

Отгадайте ребус Треугольник

Треугольник Из трёх точек состоит из века в век, Потому что так придумал человек. Не лежат при этом точки на прямой, Хоть и хочется друг к другу им домой. Три отрезка их всю жизнь соединяют. И вершинами те точки называют, А отрезки сторонами величают.

Классификация треугольников по величине углов ОстроугольныеТупоугольныеПрямоугольные Узнает очень просто меня любой дошкольник. Я тупо -, прямо -, остро – угольный треугольник.

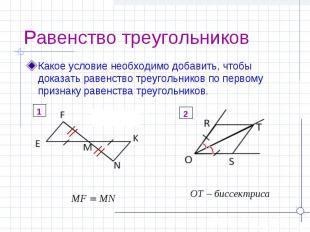
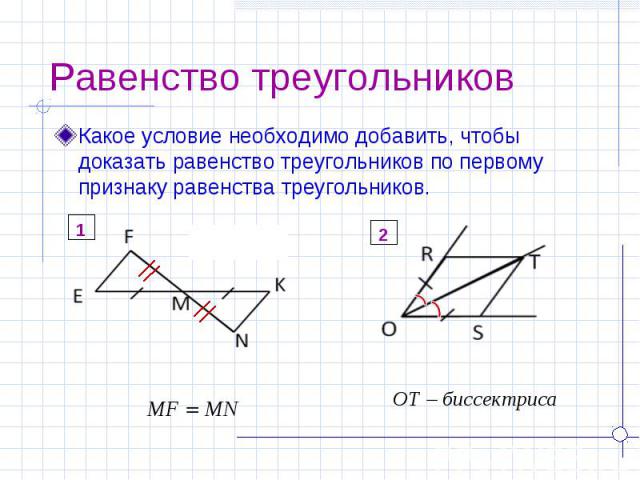
Равенство треугольников Какое условие необходимо добавить, чтобы доказать равенство треугольников по первому признаку равенства треугольников.

Треугольник – самая простая замкнутаяпрямолинейная фигура, одна из первых,свойства которой человек узнал ещё вглубокой древности. Например, то, что вравнобедренном треугольнике углы приосновании равны, было известно ещёдревним вавилонянам 4000 лет назад. Равнобедренный треугольник обладаетещё рядом геометрических свойств,которые всегда имели широкоеприменение в практической жизни.

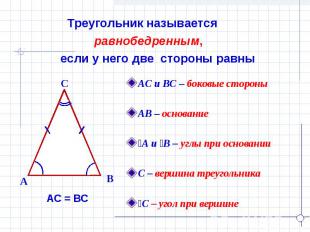
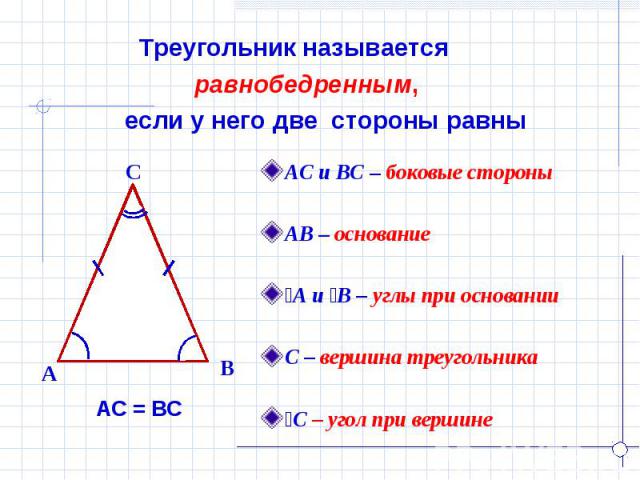
Треугольник называется равнобедренным, если у него две стороны равны АС и ВС – боковые стороныАВ – основаниеےА и ےВ – углы при основанииС – вершина треугольникаےС – угол при вершине

Равнобедренный треугольник В равнобедренном треугольнике АМК АМ = АК. Назовите основание и углы при основании этого треугольника. (МК, ےМ, ےК)Дан равнобедренный треугольник СОР c основанием СР. Назовите боковые стороны и углы при основании этого треугольника. (СО и ОР, ےС, ےР)

Какие из треугольников, изображённых на рисунке, являются равнобедренными, почему? У равнобедренных треугольников назовите: боковые стороны, основание, углы при основании, угол, противолежащий основанию (угол при вершине равнобедренного треугольника).

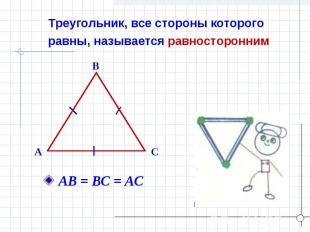
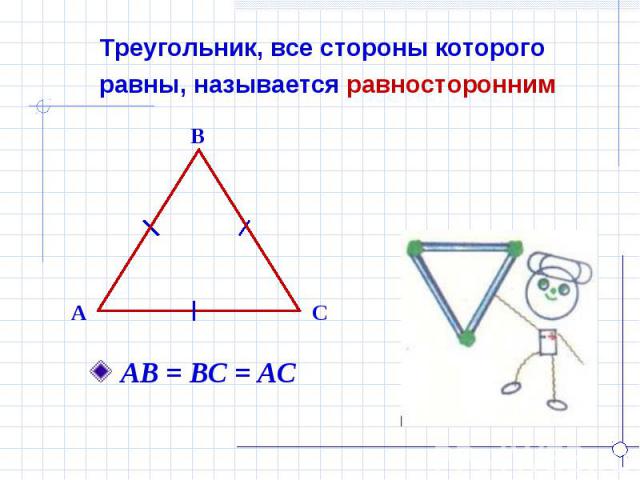
Треугольник, все стороны которого равны, называется равносторонним АВ = ВС = АС

Классификация треугольников по сторонам: разносторонние, равнобедренные, равносторонние. Зовусь я треугольник, Со мной хлопот не оберётся школьник … По – разному всегда я называюсь, Бываю я равносторонним, когда все стороны равны. Когда ж все разные даны, то я зовусь разносторонним. И если, наконец, равны две стороны,То равнобедренным я величаюсь.

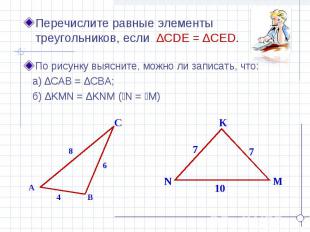
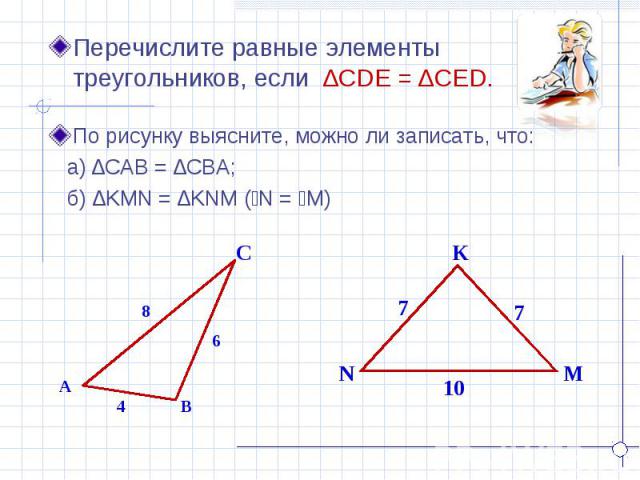
Перечислите равные элементы треугольников, если ∆CDE = ∆CED. По рисунку выясните, можно ли записать, что: а) ∆CAB = ∆CBA; б) ∆KMN = ∆KNM (ےN = ےM)

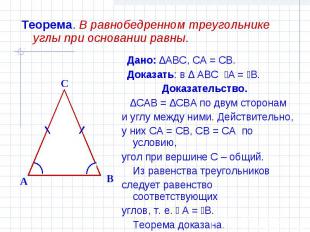
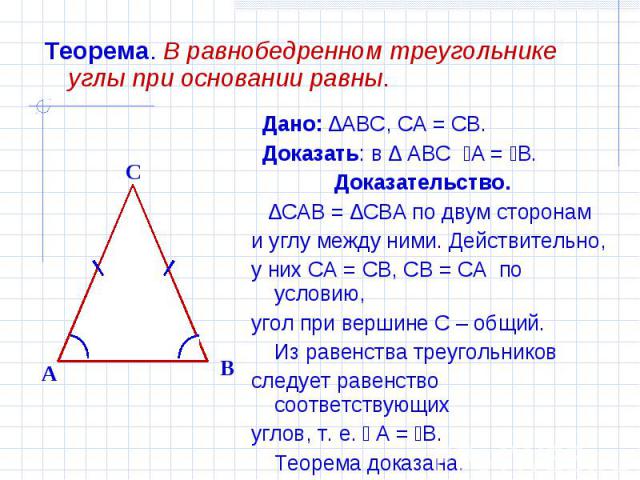
Теорема. В равнобедренном треугольнике углы при основании равны. Дано: ∆ABC, CA = CB. Доказать: в ∆ ABC ےA = ےB. Доказательство. ∆CAB = ∆CBA по двум сторонам и углу между ними. Действительно,у них CA = CB, CB = CA по условию,угол при вершине С – общий. Из равенства треугольниковследует равенство соответствующихуглов, т. е. ے А = ےВ. Теорема доказана.

В равнобедренном треугольнике боковая сторона равна 9см, а основание 5см. Вычислите периметр треугольника.В равнобедренном треугольнике основание равно 7см, а периметр равен 17см. Вычислите боковую сторону треугольника.В равнобедренном треугольнике боковая сторона равна 6см, а периметр 22см. Вычислите основание треугольника.В равностороннем треугольнике периметр равен 21см. Вычислите сторону треугольника.

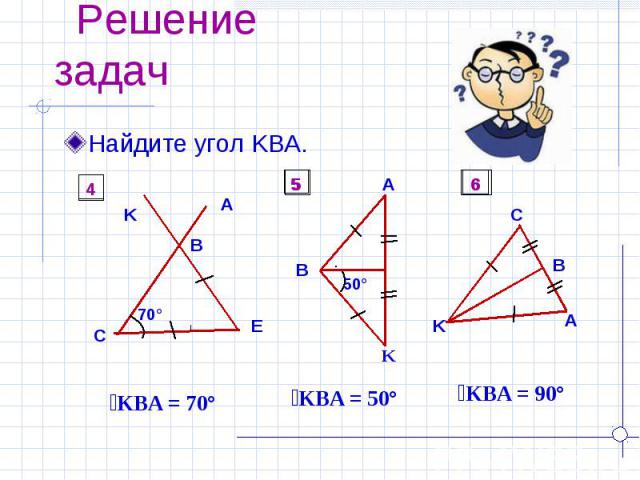
Решение задач Найдите угол KBA.

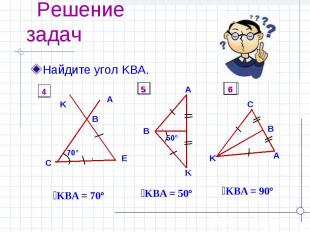
Решение задач Найдите угол KBA.

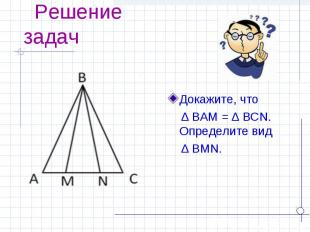
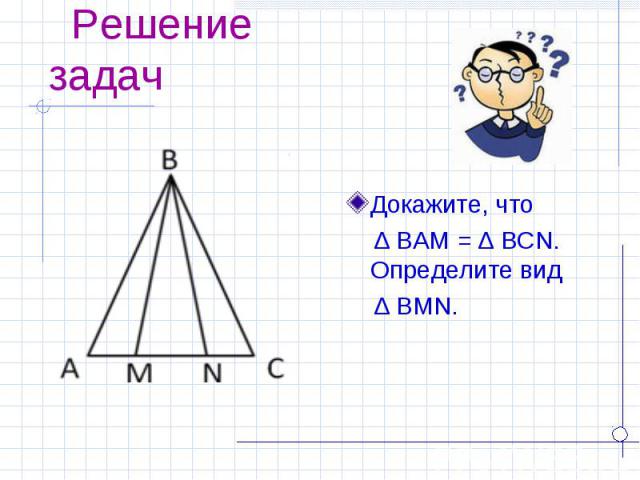
Докажите, что Докажите, что ∆ BAM = ∆ BCN. Определите вид ∆ BMN.

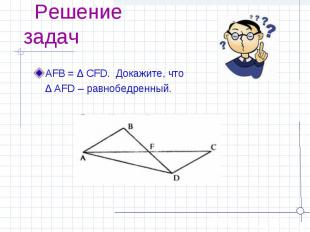
Решение задач AFB = ∆ CFD. Докажите, что ∆ AFD – равнобедренный.

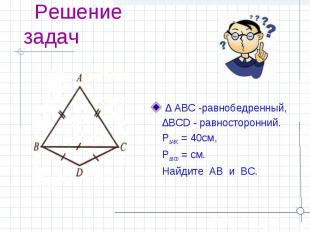
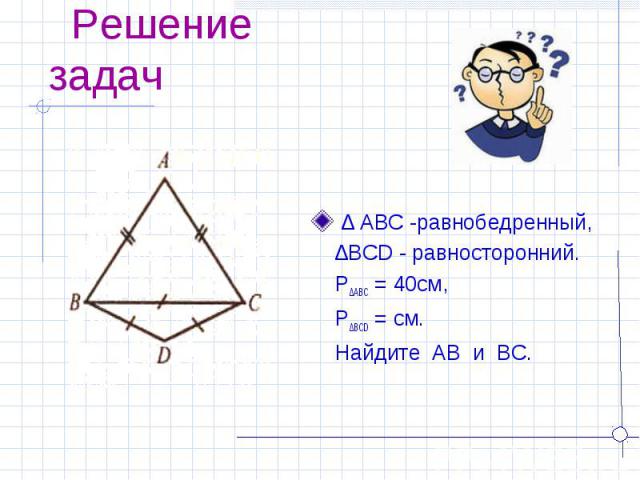
Решение задач ∆ ABC -равнобедренный, ∆BCD - равносторонний. P∆ABC = 40см, P∆BCD = см. Найдите AB и BC.

Контрольные вопросы Какой треугольник называется равнобедренным?Какой треугольник называется равносторонним?Является ли равносторонний треугольник равнобедренным?Каким свойством обладают углы в равнобедренном треугольнике?

Домашнее задание Изучить п. 23.Контрольные вопросы 3 – 5 на стр. 37.Выполнить упр. 9, 10 на стр. 39.

Удачи!

Информационные источники Литература.Погорелов А.В. Геометрия: учебник для 7 – 9 кл. общеобразовательных учреждений/ А. В. Погорелов. М.: Просвещение, 2010. Геометрия. 7 класс: поурочные планы по учебнику А. В. Погорелова/ авт. – сост. Е. П. Моисеева.- Волгоград: Учитель, 2006. Геометрия в 6 классе: Пособие для учителей/ Н. Б. Мельникова, И. Л. Никольская, Л. Ю. Чернышева. – М.: Просвещение, 1982. Геометрия. Рабочая тетрадь для 7 класса/Мищенко Т. М. – М.: Издательский Дом «Генжер»,2000. Тематический контроль по геометрии. 7 -9 класс/Мищенко Т. М. – М.: Издательский Дом «Генжер», 1997 Интернет – ресурсы.www.testent.ru http://www.uchportal.ru/load/24-1-0-22420festival.1september.ru/articles/534282/