Презентация на тему: Сферические координаты

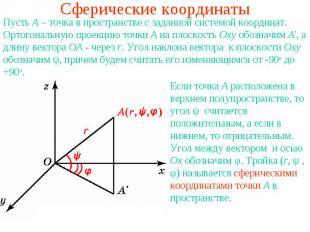
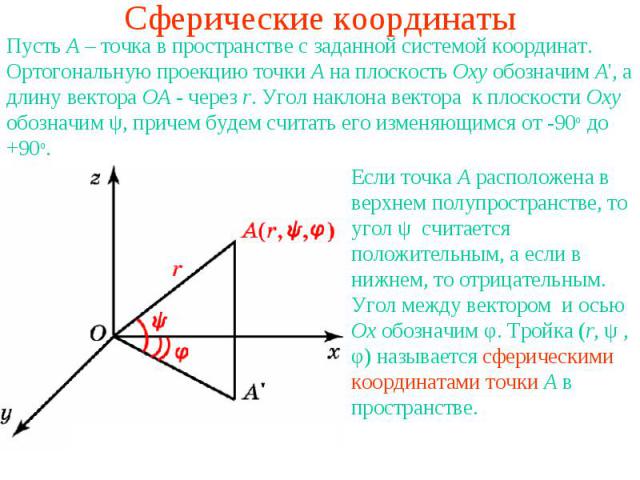
Сферические координатыПусть A – точка в пространстве с заданной системой координат. Ортогональную проекцию точки A на плоскость Oxy обозначим A', а длину вектора ОA - через r. Угол наклона вектора к плоскости Оxy обозначим ψ, причем будем считать его изменяющимся от -90o до +90o. Если точка A расположена в верхнем полупространстве, то угол ψ считается положительным, а если в нижнем, то отрицательным. Угол между вектором и осью Ox обозначим φ. Тройка (r, ψ , φ) называется сферическими координатами точки A в пространстве.

Сферические координатыДекартовы координаты (x,y,z) точки в пространстве выражаются через ее сферические координаты по формулами, наоборот, если заданы декартовы координаты, то по ним можно найти сферические координаты по формулам

Сферические координатыТочки на сфере, имеющие одинаковый угол ψ, образуют окружность, которая называется параллелью. Точки, имеющие одинаковый угол φ, образуют полуокружность, называемую меридианом.Дуга большой окружности, соединяющая две точки сферы, является кратчайшим путем на сфере между этими двумя точками. Такой путь называют ортодромией, что в переводе с греческого означает "прямой бег".Кривая, образующая равные углы с разными меридианами, называется локсодромия, что в переводе с греческого означает "косой бег".

Упражнение 1 Найдите декартовы координаты следующих точек пространства, заданных своими сферическими координатами: (1,45°,120°), (2,-30°,-90°), (1,90°, 60°).

Упражнение 2 Найдите сферические координаты следующих точек пространства, заданных своими декартовыми координатами: A(1,1,1), B(-1,0,1), C(0,0,2).

Упражнение 3 Найдите сферические координаты вершин куба, задаваемого в декартовых координатах системой неравенств

Упражнение 4 Точка A имеет сферические координаты (r, , ). Найдите сферические координаты точки, симметричной данной, относительно: а) координатных плоскостей; б) осей координат; в) начала координат.

Упражнение 5 Найдите геометрическое место точек пространства, сферические координаты которых удовлетворяют условиям: а) r постоянно; б) постоянно; в) постоянно.

Упражнение 6 Какая фигура в пространстве задается неравенствами: а) 0 r 1, 0 ; б) 0 r 1, 0 ; в) 0 r 1, 0 , 0 ?

Упражнение 7 Найдите расстояние между точками, заданными своими сферическими координатами: A( ,0°,45°), B(2,60°,0°).

Упражнение 8 Где закончится локсодромия, образующая острый угол с меридианами, при ее продолжении в обе стороны?

Упражнение 9 Напишите уравнение сферы в сферических координатах

Упражнение 10 Найдите длины дуг локсодромии и ортодромии, соединяющих точки A1(R, 45°, 0°), A2(R, 45°, 180°) на сфере.