Презентация на тему: Прямоугольная система координат

Прямоугольная система координатПрямоугольной системой координат в пространстве называется тройка взаимно перпендикулярных координатных прямых с общим началом координат. Общее начало координат обозначается буквой O, а координатные прямые обозначаются Ox, Oy, Oz и называются соответственно осью абсцисс, осью ординат и осью аппликат . Плоскости, проходящие через пары координатных прямых, называются координатными плоскостями и обозначаются Oxy, Oxz и Oyz соответственно.

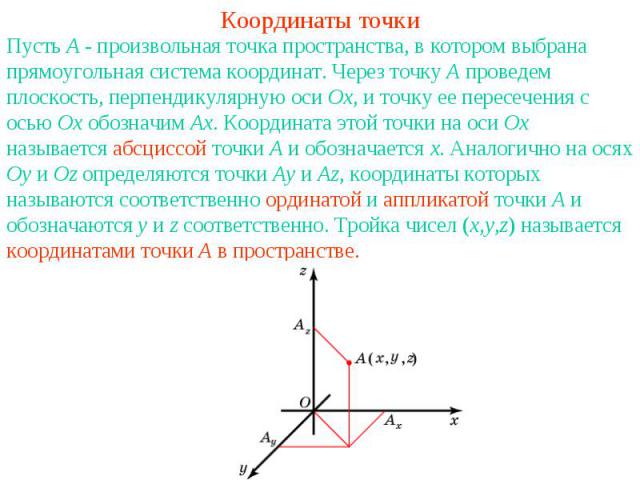
Координаты точкиПусть A - произвольная точка пространства, в котором выбрана прямоугольная система координат. Через точку A проведем плоскость, перпендикулярную оси Ox, и точку ее пересечения с осью Ox обозначим Ax. Координата этой точки на оси Ox называется абсциссой точки A и обозначается x. Аналогично на осях Oy и Oz определяются точки Ay и Az, координаты которых называются соответственно ординатой и аппликатой точки A и обозначаются y и z соответственно. Тройка чисел (x,y,z) называется координатами точки A в пространстве.

Упражнение 1Найдите координаты ортогональных проекций точек A(1,3,4) и B(5,-6,2) на: а) плоскость Oxy; б) плоскость Oyz; в) ось Ox; г) ось Oz.Ответ: а) (1,3,0), (5,-6,0); б) (0,3,4), (0,-6,2); в) (1,0,0), (5,0,0); г) (0,0,4), (0,0,2).

Упражнение 2Что представляет собой геометрическое место точек пространства, для которых: а) первая координата равна нулю; б) вторая координата равна нулю; в) третья координата равна нулю; г) первая и вторая координаты равны нулю; д) первая и третья координаты равны нулю; е) вторая и третья координаты равны нулю; ж) все координаты равны нулю?

Упражнение 3На каком расстоянии находится точка A(1,-2,3) от координатной плоскости: а) Oxy; б) Oxz; в) Oyz?

Упражнение 4На каком расстоянии находится точка A(1,-2,3) от координатной прямой: а) Ox; б) Oy; в) Oz?

Упражнение 5Каким является геометрическое место точек пространства, для которых: а) первая координата равна единице; б) первая и вторая координаты равны единице?Ответ: а) Плоскость, параллельная плоскости Oyz и проходящая через точку (1,0,0); б) прямая, параллельная оси Oz и и проходящая через точку (1,1,0).

Упражнение 6Какому условию удовлетворяют координаты точек пространства, одинаково удаленные от: а) двух координатных плоскостей Oxy, Oyz; б) всех трех координатных плоскостей?

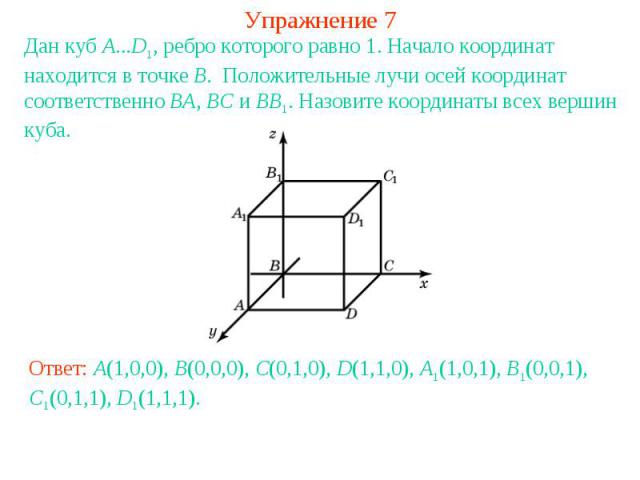
Упражнение 7Дан куб A...D1, ребро которого равно 1. Начало координат находится в точке B. Положительные лучи осей координат соответственно BA, BC и BB1. Назовите координаты всех вершин куба.Ответ: A(1,0,0), B(0,0,0), C(0,1,0), D(1,1,0), A1(1,0,1), B1(0,0,1), C1(0,1,1), D1(1,1,1).

Упражнение 8Куб A...D1 помещен в прямоугольную систему координат так, что началом координат является центр нижнего основания куба, ребра куба параллельны соответствующим осям координат, вершина A имеет координаты (-2,2,0). Найдите координаты всех остальных вершин куба.Ответ: B(-2,-2,0), C(2,-2,0), D(2,2,0), A1(-2,2,4), B1(-2,-2,4), C1(2,-2,4), D1(2,2,4).
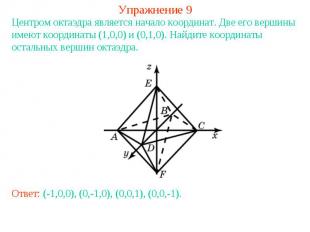
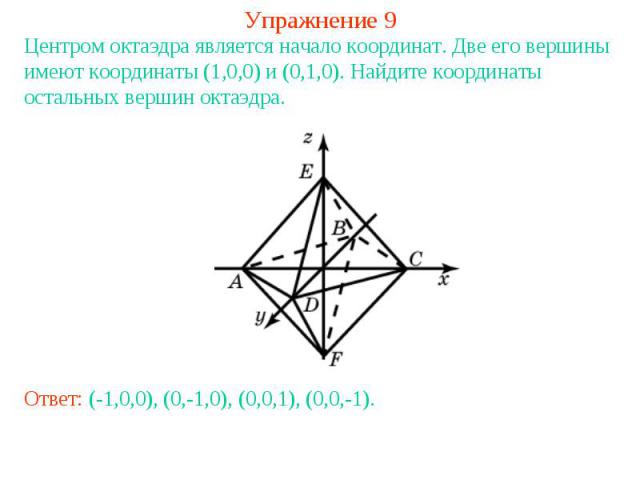
Упражнение 9Центром октаэдра является начало координат. Две его вершины имеют координаты (1,0,0) и (0,1,0). Найдите координаты остальных вершин октаэдра.Ответ: (-1,0,0), (0,-1,0), (0,0,1), (0,0,-1).

Упражнение 10Как расположена сфера радиуса 2 с центром в точке с координатами (1,2,3) относительно координатных плоскостей?Ответ: Не имеет общих точек с координатной плоскостью Oxz; касается координатной плоскости Oxz; пересекает координатную плоскость Oyz.

Упражнение 11Точка A имеет координаты (x, y, z). Найдите координаты симметричной точки относительно: а) координатных плоскостей; б) координатных прямых; в) начала координат.

Упражнение 12Найдите координаты середины отрезка: а) AB, если A(1,2,3) и B(-1,0,1); б) CD, если C(3,3,0) и D(3,-1,2).