Презентация на тему: Ориентация поверхности
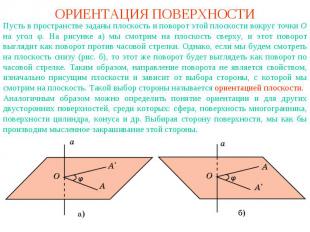
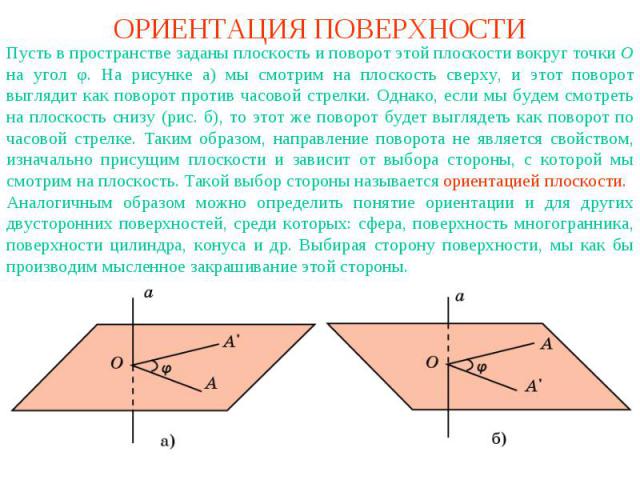
ОРИЕНТАЦИЯ ПОВЕРХНОСТИПусть в пространстве заданы плоскость и поворот этой плоскости вокруг точки О на угол φ. На рисунке а) мы смотрим на плоскость сверху, и этот поворот выглядит как поворот против часовой стрелки. Однако, если мы будем смотреть на плоскость снизу (рис. б), то этот же поворот будет выглядеть как поворот по часовой стрелке. Таким образом, направление поворота не является свойством, изначально присущим плоскости и зависит от выбора стороны, с которой мы смотрим на плоскость. Такой выбор стороны называется ориентацией плоскости.Аналогичным образом можно определить понятие ориентации и для других двусторонних поверхностей, среди которых: сфера, поверхность многогранника, поверхности цилиндра, конуса и др. Выбирая сторону поверхности, мы как бы производим мысленное закрашивание этой стороны.
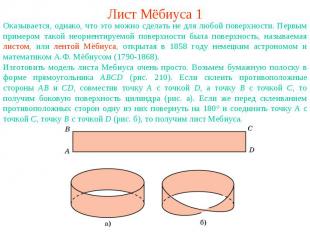
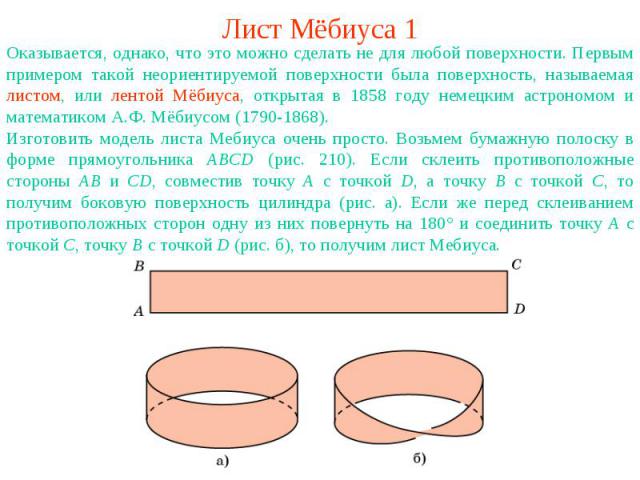
Лист Мёбиуса 1Оказывается, однако, что это можно сделать не для любой поверхности. Первым примером такой неориентируемой поверхности была поверхность, называемая листом, или лентой Мёбиуса, открытая в 1858 году немецким астрономом и математиком А.Ф. Мёбиусом (1790-1868). Изготовить модель листа Мебиуса очень просто. Возьмем бумажную полоску в форме прямоугольника АВСD (рис. 210). Если склеить противоположные стороны АВ и CD, совместив точку А с точкой D, а точку В с точкой С, то получим боковую поверхность цилиндра (рис. а). Если же перед склеиванием противоположных сторон одну из них повернуть на 180° и соединить точку A с точкой C, точку B с точкой D (рис. б), то получим лист Мебиуса.

Лист Мёбиуса 2Лист Мёбиуса имеет только одну сторону. Муравью, ползущему по листу Мебиуса, не надо переползать через его край, чтобы попасть на противоположную сторону, как это видно на гравюре М. Эшера.Свойство односторонности листа Мебиуса используется при изготовлении ременных передач. Если ремень сделать в виде ленты Мебиуса, то он будет изнашиваться вдвое медленнее, чем обычный. Это объясняется тем, что в работе ремня, изготовленного в виде ленты Мебиуса, принимает участие вся поверхность, а не только внутренняя ее часть, как у обычной ременной передачи.

Упражнение 1Является ли ориентируемой: а) сфера; б) боковая поверхность цилиндра; в) поверхность конуса?

Упражнение 2Сколько сторон имеет тор (напомним, это поверхность, полученная вращением окружности вокруг прямой, лежащей в плоскости окружности и не пересекающей эту окружность)?

Упражнение 3Является ли ориентируемой поверхностью: а) дважды перекрученная лента; б) трижды перекрученная лента?
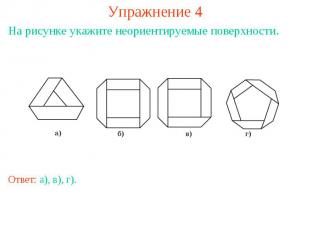
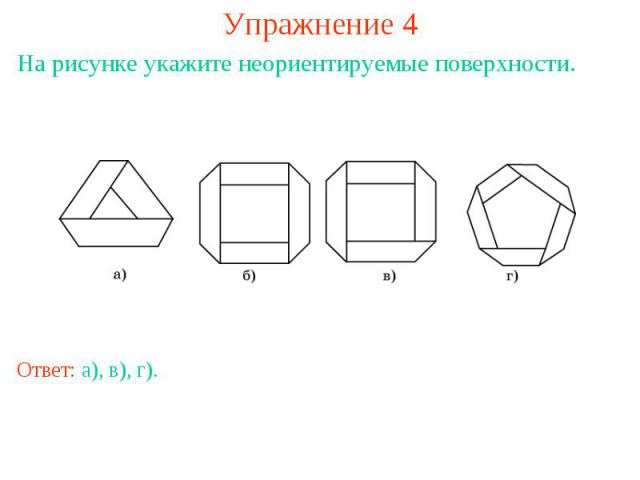
Упражнение 4На рисунке укажите неориентируемые поверхности.

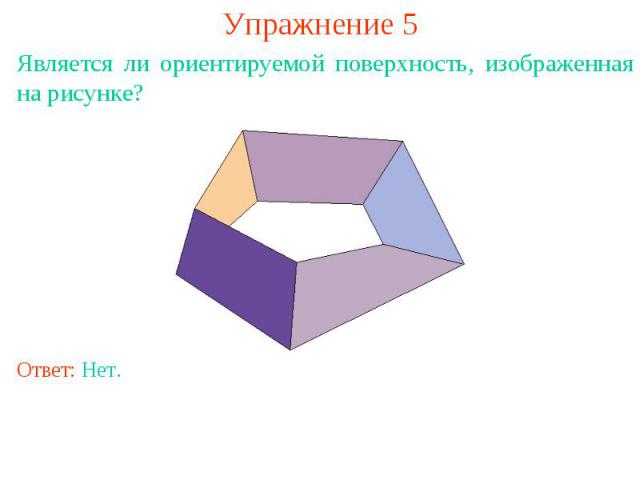
Упражнение 5Является ли ориентируемой поверхность, изображенная на рисунке?

Упражнение 6Сколько сторон имеет поверхность, полученная при разрезании листа Мебиуса по средней линии?

Упражнение 7Что получится, если дважды перекрученную ленту разрезать по средней линии?

Упражнение 8Что получится, если лист Мебиуса разрезать не по средней линии, а отступив от края на треть ширины ленты?

Упражнение 9Отрезок AB, параллельный прямой a, вращается вокруг этой прямой и одновременно вращается вокруг своего центра в плоскости отрезка AB и прямой a. За время полного оборота вокруг прямой a отрезок совершает поворот на 180° вокруг своего центра?

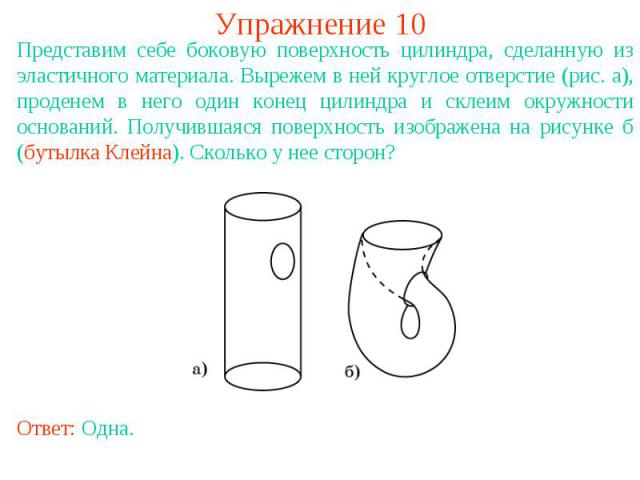
Упражнение 10Представим себе боковую поверхность цилиндра, сделанную из эластичного материала. Вырежем в ней круглое отверстие (рис. а), проденем в него один конец цилиндра и склеим окружности оснований. Получившаяся поверхность изображена на рисунке б (бутылка Клейна). Сколько у нее сторон?
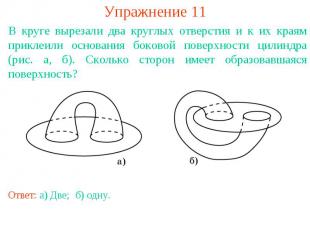
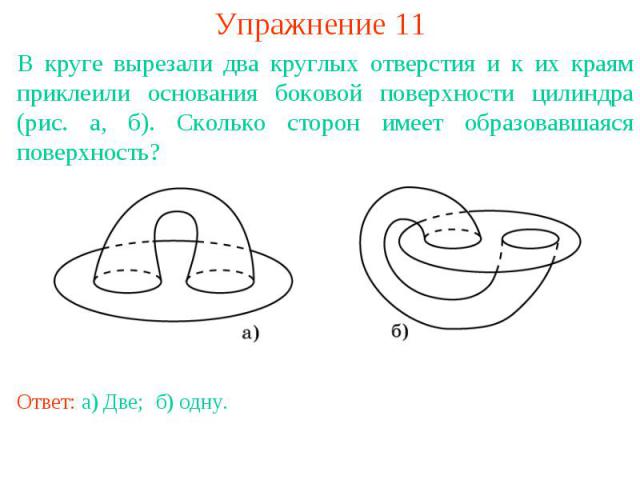
Упражнение 11В круге вырезали два круглых отверстия и к их краям приклеили основания боковой поверхности цилиндра (рис. а, б). Сколько сторон имеет образовавшаяся поверхность?

Упражнение 12Сколько сторон имеет поверхность, изображенная на рисунке? Является ли она ориентируемой?