Презентация на тему: Центральная симметрия

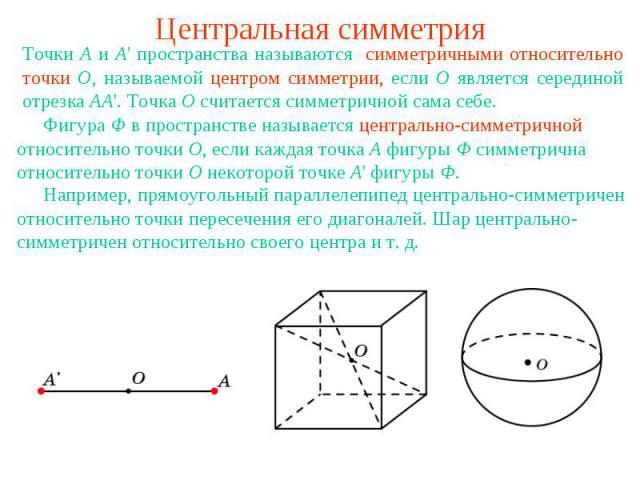
Центральная симметрияТочки A и A' пространства называются симметричными относительно точки O, называемой центром симметрии, если O является серединой отрезка AA'. Точка O считается симметричной сама себе. Фигура Ф в пространстве называется центрально-симметричной относительно точки O, если каждая точка A фигуры Ф симметрична относительно точки O некоторой точке A' фигуры Ф. Например, прямоугольный параллелепипед центрально-симметричен относительно точки пересечения его диагоналей. Шар центрально-симметричен относительно своего центра и т. д.

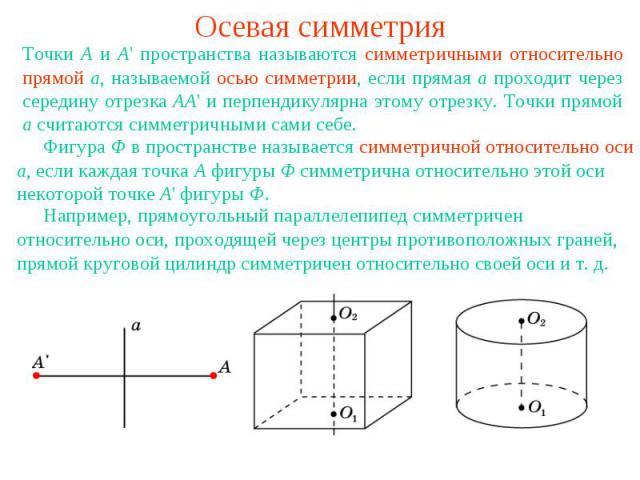
Осевая симметрияТочки A и A' пространства называются симметричными относительно прямой a, называемой осью симметрии, если прямая a проходит через середину отрезка AA' и перпендикулярна этому отрезку. Точки прямой a считаются симметричными сами себе. Фигура Ф в пространстве называется симметричной относительно оси a, если каждая точка A фигуры Ф симметрична относительно этой оси некоторой точке A' фигуры Ф. Например, прямоугольный параллелепипед симметричен относительно оси, проходящей через центры противоположных граней, прямой круговой цилиндр симметричен относительно своей оси и т. д.

Зеркальная симметрияТочки A и A' в пространстве называются симметричными относительно плоскости α, называемой плоскостью симметрии, если эта плоскость проходит через середину отрезка AA' и перпендикулярна к нему. Точки плоскости α считаются симметричными сами себе. Симметрия относительно плоскости называется также зеркальной симметрией. Фигура Ф в пространстве называется зеркально-симметричной относительно плоскости α, если каждая точка A фигуры Ф симметрична относительно этой плоскости некоторой точке A' фигуры Ф. Например, прямоугольный параллелепипед зеркально-симметричен относительно плоскости, проходящей через ось симметрии и параллельной одной из граней. Цилиндр зеркально-симметричен относительно любой плоскости, проходящей через его ось и т. д.

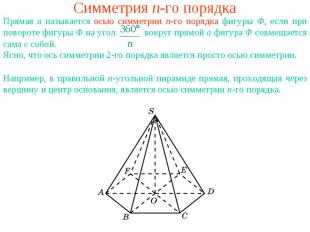
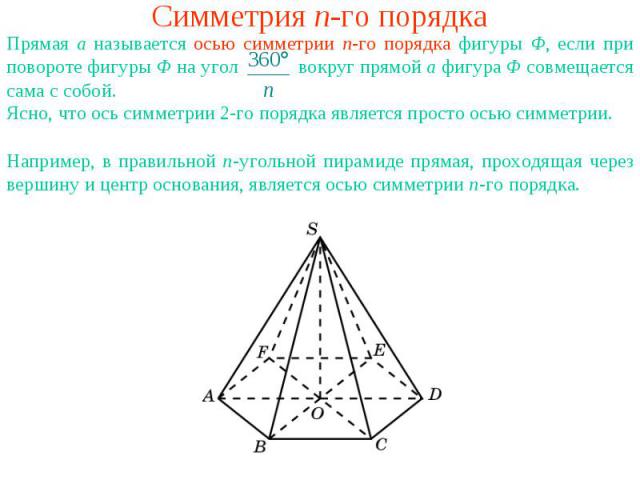
Симметрия n-го порядкаПрямая a называется осью симметрии n-го порядка фигуры Ф, если при повороте фигуры Ф на угол вокруг прямой a фигура Ф совмещается сама с собой.Ясно, что ось симметрии 2-го порядка является просто осью симметрии.Например, в правильной n-угольной пирамиде прямая, проходящая через вершину и центр основания, является осью симметрии n-го порядка.

Упражнение 1Приведите примеры центрально-симметричных и не центрально-симметричных фигур.Ответ: Центрально-симметричные: куб, прямоугольный параллелепипед, шар и др.; не центрально-симметричные: пирамида, конус и др.

Упражнение 2Может ли центр симметрии фигуры не принадлежать ей?

Упражнение 3Может ли фигура иметь более одного центра симметрии?

Упражнение 4Может ли фигура иметь ровно два центра симметрии?

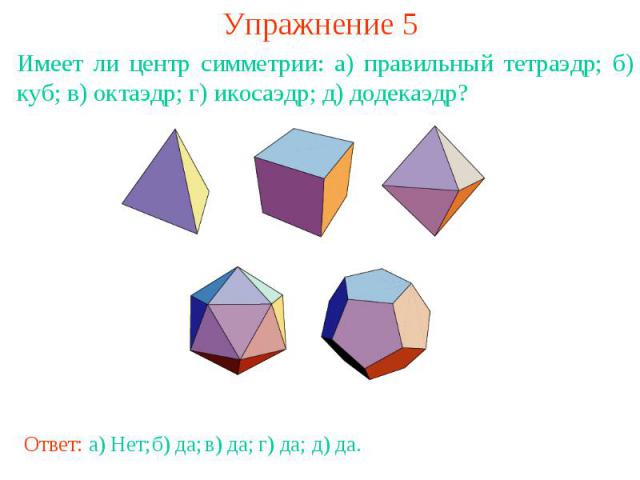
Упражнение 5Имеет ли центр симметрии: а) правильный тетраэдр; б) куб; в) октаэдр; г) икосаэдр; д) додекаэдр?

Упражнение 6Имеет ли центр симметрии наклонная призма, основанием которой является правильный девятиугольник?

Упражнение 7Сколько осей симметрии имеет прямоугольный параллелепипед?

Упражнение 8Сколько осей симметрии имеет шар?

Упражнение 9Приведите примеры пространственных фигур с осями симметрии 3-го, 4-го и т. д. порядков.

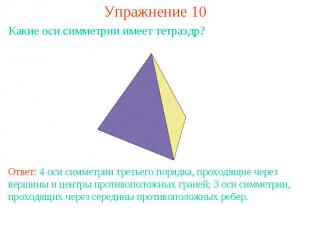
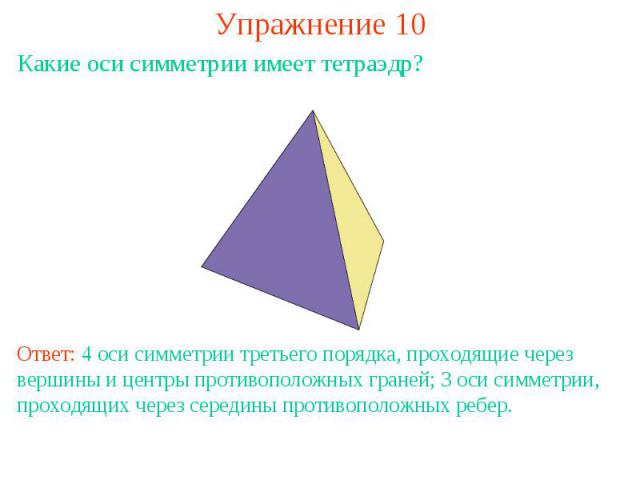
Упражнение 10Какие оси симметрии имеет тетраэдр?Ответ: 4 оси симметрии третьего порядка, проходящие через вершины и центры противоположных граней; 3 оси симметрии, проходящих через середины противоположных ребер.

Упражнение 11Какие оси симметрии имеет куб?Ответ: 4 оси симметрии третьего порядка, проходящие через противоположные вершины; 6 осей симметрии, проходящих через середины противоположных ребер; 3 оси симметрии, проходящие через центры противоположных граней.

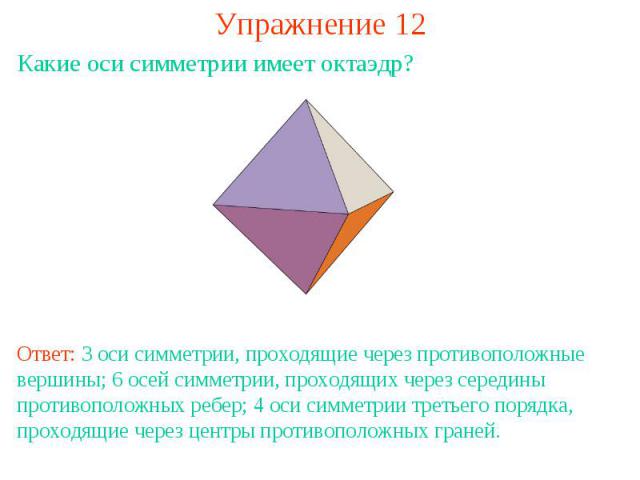
Упражнение 12Какие оси симметрии имеет октаэдр?Ответ: 3 оси симметрии, проходящие через противоположные вершины; 6 осей симметрии, проходящих через середины противоположных ребер; 4 оси симметрии третьего порядка, проходящие через центры противоположных граней.

Упражнение 13Какие оси симметрии имеет икосаэдр?Ответ: 6 осей симметрии пятого порядка, проходящих через противоположные вершины; 15 осей симметрии, проходящих через середины противоположных ребер; 10 осей симметрии третьего порядка, проходящие через центры противоположных граней.

Упражнение 14Какие оси симметрии имеет додекаэдр?Ответ: 10 осей симметрии третьего порядка, проходящих через противоположные вершины; 15 осей симметрии, проходящих через середины противоположных ребер; 6 осей симметрии пятого порядка, проходящие через центры противоположных граней.

Упражнение 15Приведите пример фигуры, имеющей центр симметрии, но не имеющей оси симметрии.

Упражнение 16Приведите пример фигуры, имеющей ось симметрии, но не имеющей центра симметрии.

Упражнение 17Найдите центр, оси и плоскости симметрии фигуры, состоящей из двух пересекающихся прямых.Ответ: Центр симметрии – точка пересечения данных прямых. Оси симметрии – две прямые, содержащие биссектрисы углов, образованные данными прямыми, и прямая, проходящая через точку пересечения данных прямых и перпендикулярная их плоскости. Если данные прямые перпендикулярны, то сами они также являются осями симметрии. Плоскости симметрии: плоскость данных прямых и две плоскости, проходящие через биссектрисы углов, образованные данными прямыми и перпендикулярные их плоскости.

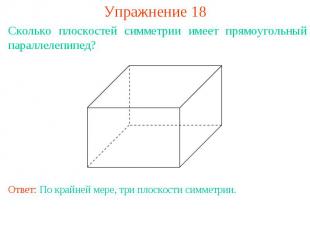
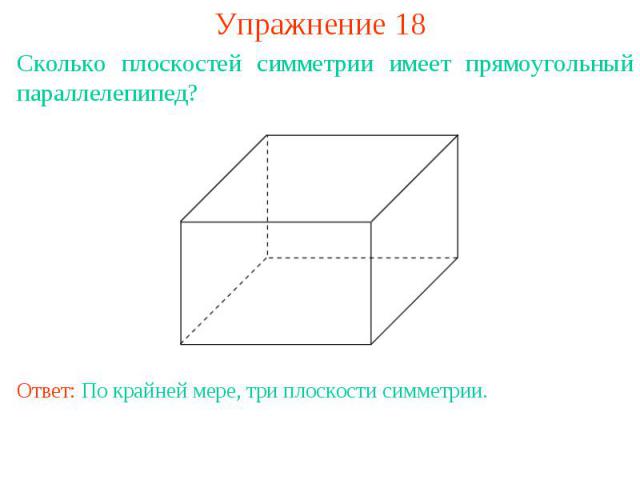
Упражнение 18Сколько плоскостей симметрии имеет прямоугольный параллелепипед?Ответ: По крайней мере, три плоскости симметрии.

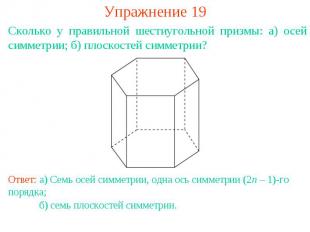
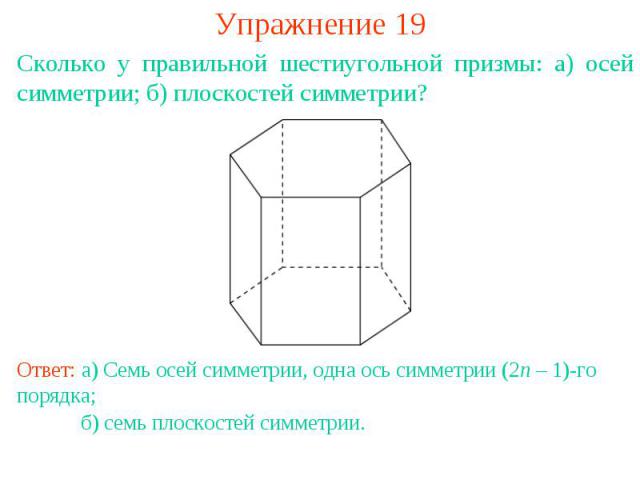
Упражнение 19Сколько у правильной шестиугольной призмы: а) осей симметрии; б) плоскостей симметрии?Ответ: а) Семь осей симметрии, одна ось симметрии (2n – 1)-го порядка; б) семь плоскостей симметрии.

Упражнение 20В основании прямой призмы лежит ромб. Сколько она имеет: а) осей симметрии; б) плоскостей симметрии?

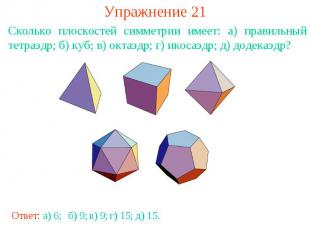
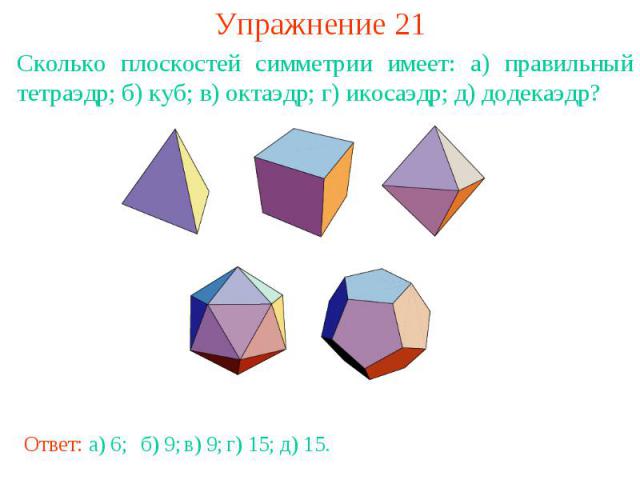
Упражнение 21Сколько плоскостей симметрии имеет: а) правильный тетраэдр; б) куб; в) октаэдр; г) икосаэдр; д) додекаэдр?

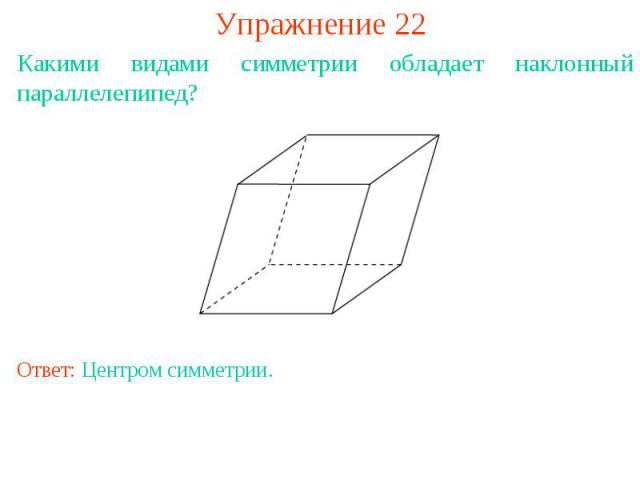
Упражнение 22Какими видами симметрии обладает наклонный параллелепипед?

Упражнение 23Приведите примеры пространственных фигур, у которых есть ось симметрии, но нет плоскости симметрии и, наоборот, есть плоскость симметрии, но нет оси симметрии.Ответ: Пирамида, в основании которой параллелограмм, может иметь ось симметрии, но не имеет плоскости симметрии. Правильная треугольная пирамида имеет плоскости симметрии, но не имеет осей симметрии.