Презентация на тему: Определение гиперболы
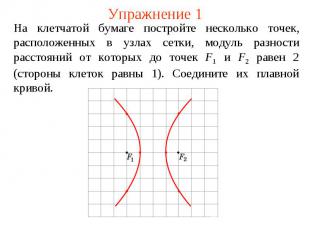
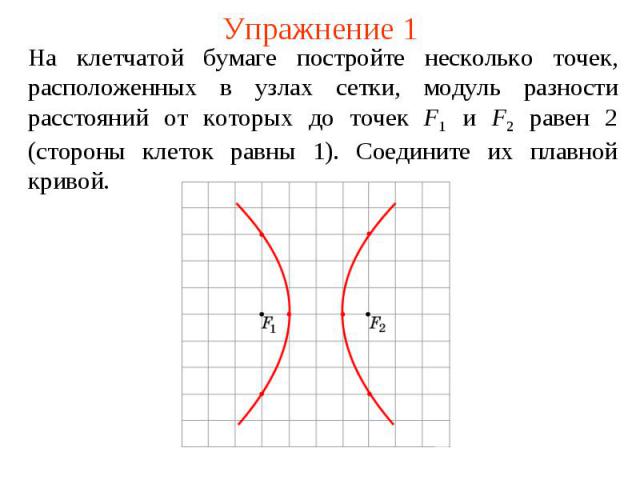
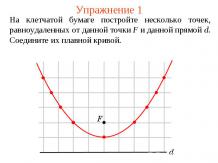
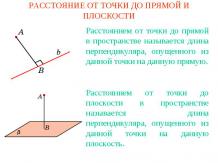
Упражнение 1На клетчатой бумаге постройте несколько точек, расположенных в узлах сетки, модуль разности расстояний от которых до точек F1 и F2 равен 2 (стороны клеток равны 1). Соедините их плавной кривой.
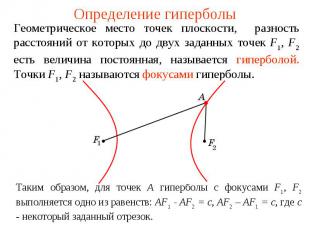
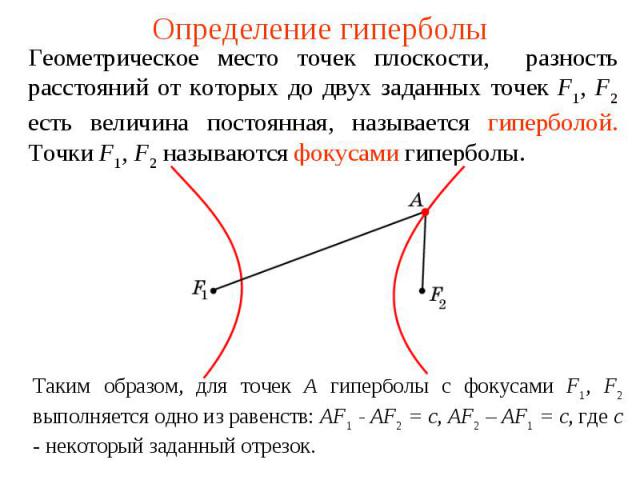
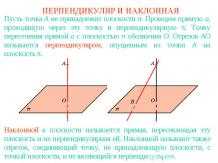
Определение гиперболыГеометрическое место точек плоскости, разность расстояний от которых до двух заданных точек F1, F2 есть величина постоянная, называется гиперболой. Точки F1, F2 называются фокусами гиперболы. Таким образом, для точек А гиперболы с фокусами F1, F2 выполняется одно из равенств: AF1 - AF2 = c, AF2 – AF1 = c, где c - некоторый заданный отрезок.

Упражнение 2Найдите геометрическое место точек A, для которых разность AF1 – AF2 расстояний до двух заданных точек F1, F2: а) больше заданной величины c; б) меньше заданной величины c.Ответ: а) Точки A’, расположенные внутри ветви гиперболы;б) точки A”, расположенные вне ветви гиперболы.
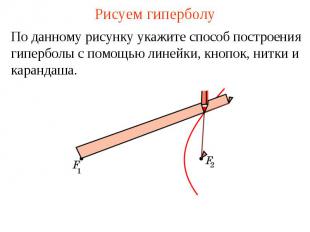
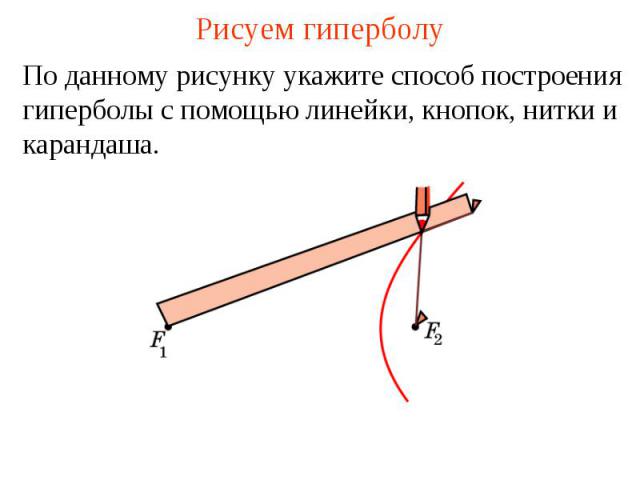
Рисуем гиперболуПо данному рисунку укажите способ построения гиперболы с помощью линейки, кнопок, нитки и карандаша.
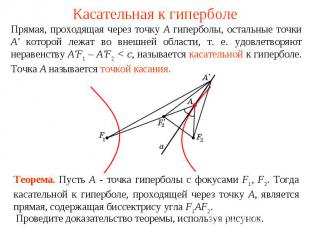
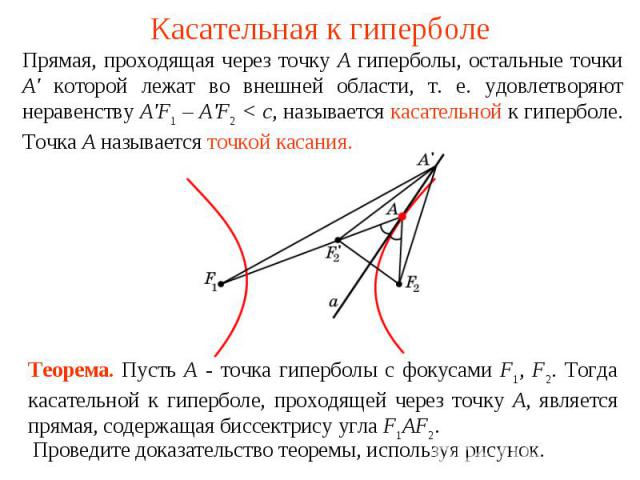
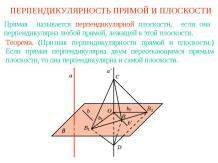
Касательная к гиперболеПрямая, проходящая через точку А гиперболы, остальные точки A' которой лежат во внешней области, т. е. удовлетворяют неравенству A'F1 – A'F2 < c, называется касательной к гиперболе. Точка А называется точкой касания. Теорема. Пусть А - точка гиперболы с фокусами F1, F2. Тогда касательной к гиперболе, проходящей через точку A, является прямая, содержащая биссектрису угла F1AF2.Проведите доказательство теоремы, используя рисунок.
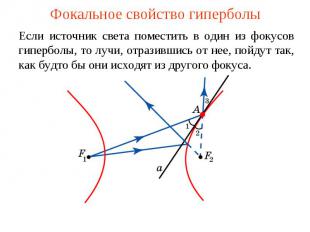
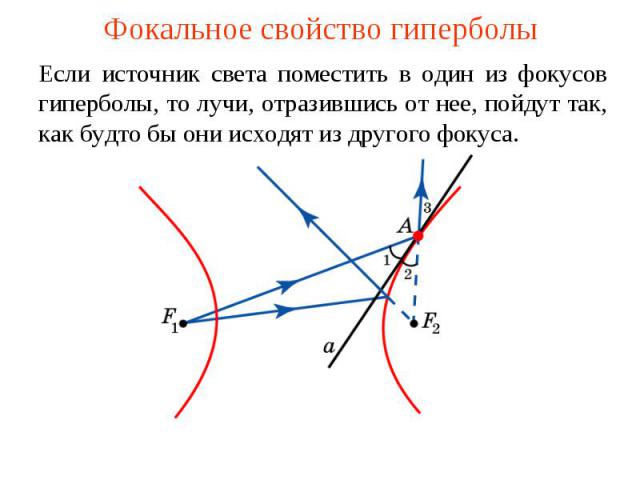
Фокальное свойство гиперболыЕсли источник света поместить в один из фокусов гиперболы, то лучи, отразившись от нее, пойдут так, как будто бы они исходят из другого фокуса.
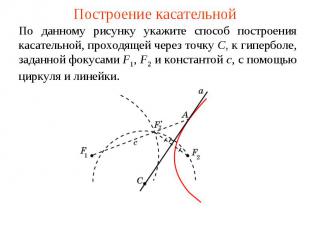
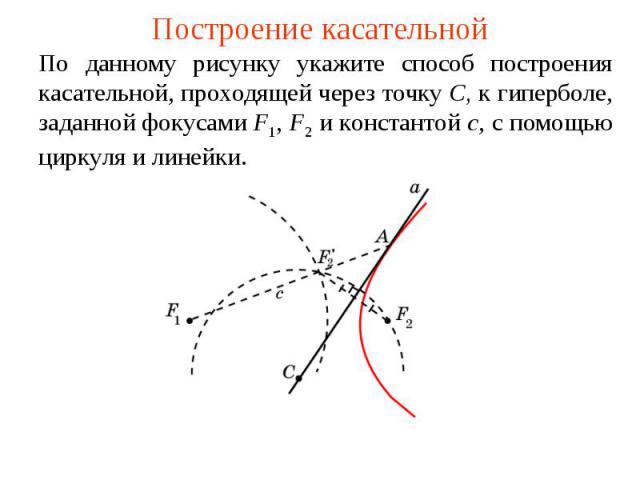
Построение касательнойПо данному рисунку укажите способ построения касательной, проходящей через точку C, к гиперболе, заданной фокусами F1, F2 и константой c, с помощью циркуля и линейки.

Упражнение 3Сколько касательных можно провести к одной ветви гиперболы из точки: а) принадлежащей ветви гиперболы; б) лежащей вне ветви гиперболы; в) лежащей внутри ветви гиперболы?
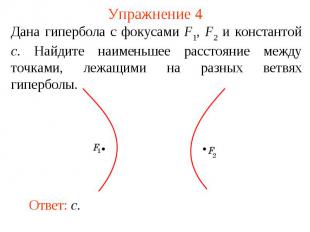
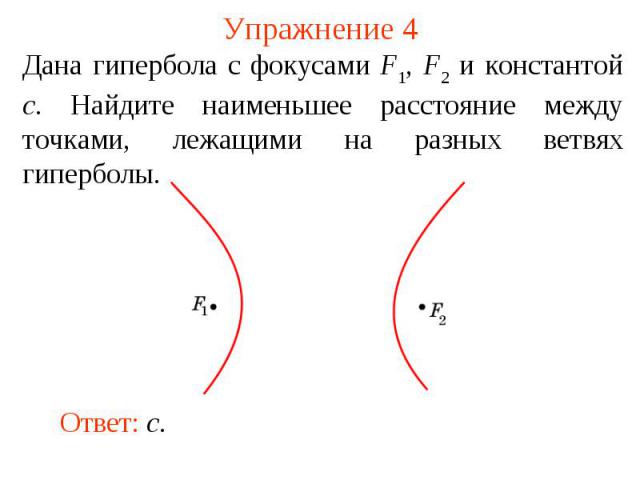
Упражнение 4Дана гипербола с фокусами F1, F2 и константой c. Найдите наименьшее расстояние между точками, лежащими на разных ветвях гиперболы.
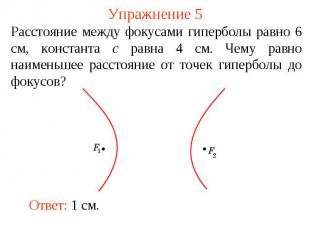
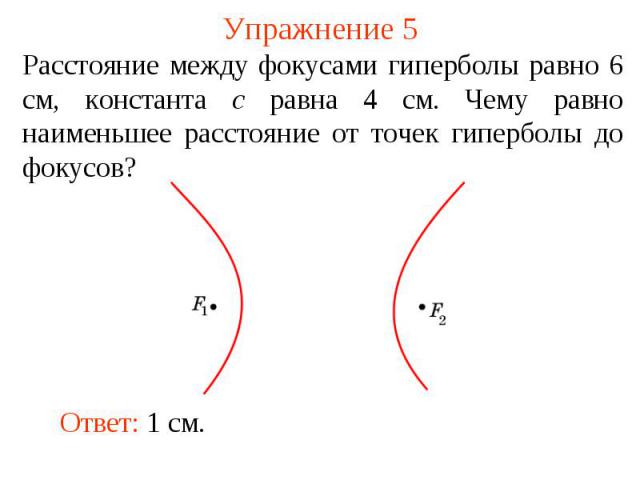
Упражнение 5Расстояние между фокусами гиперболы равно 6 см, константа c равна 4 см. Чему равно наименьшее расстояние от точек гиперболы до фокусов?
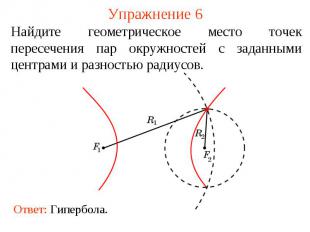
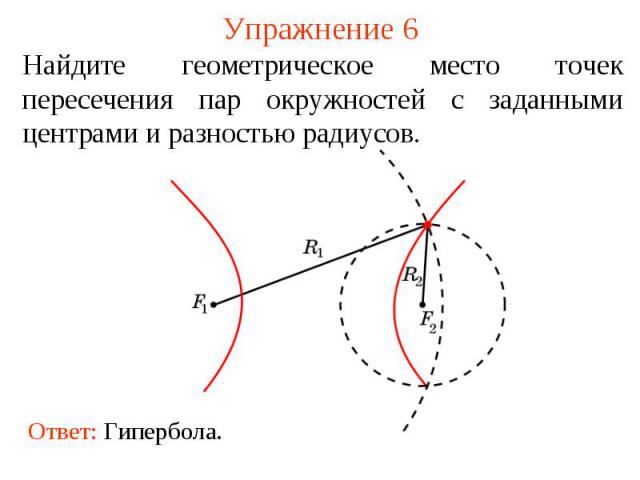
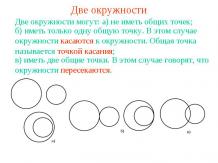
Упражнение 6Найдите геометрическое место точек пересечения пар окружностей с заданными центрами и разностью радиусов.
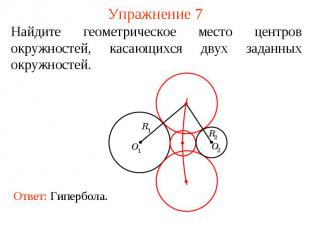
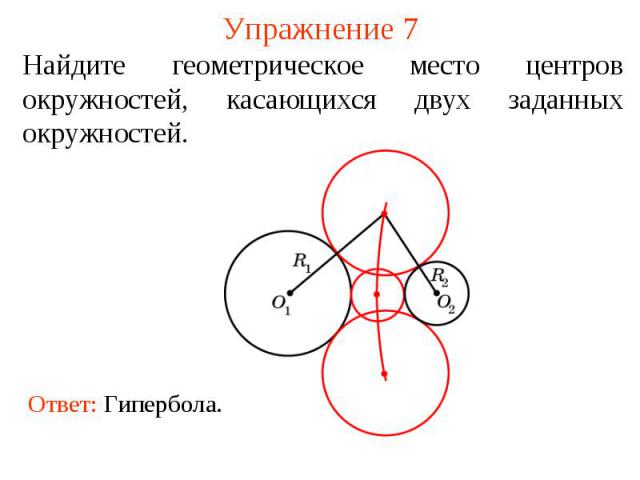
Упражнение 7Найдите геометрическое место центров окружностей, касающихся двух заданных окружностей.

Упражнение 8Что будет происходить с гиперболой, если константа c не изменяется, а фокусы: а) приближаются друг к другу; б) удаляются друг от друга?Ответ: а) Ветви гиперболы сжимаются; б) ветви гиперболы расширяются.
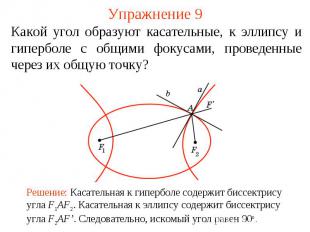
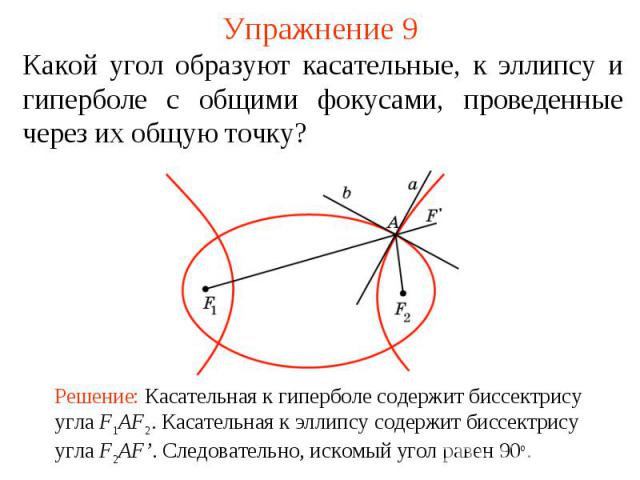
Упражнение 9Какой угол образуют касательные, к эллипсу и гиперболе с общими фокусами, проведенные через их общую точку?Решение: Касательная к гиперболе содержит биссектрису угла F1AF2. Касательная к эллипсу содержит биссектрису угла F2AF’. Следовательно, искомый угол равен 90о.