Презентация на тему: Окружность

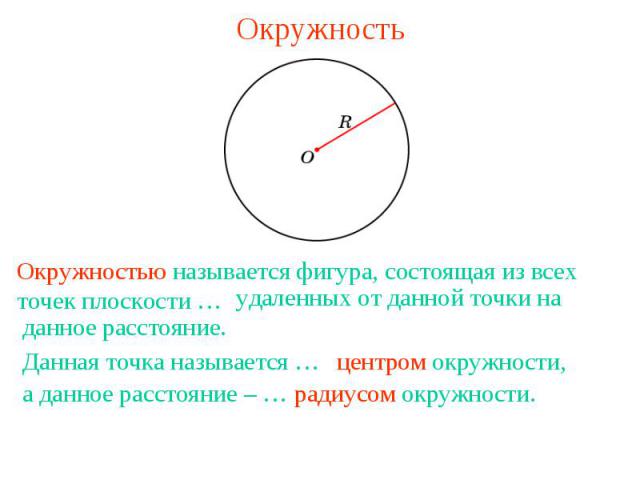
ОкружностьОкружностью называется фигура, состоящая из всех точек плоскости … удаленных от данной точки на данное расстояние.

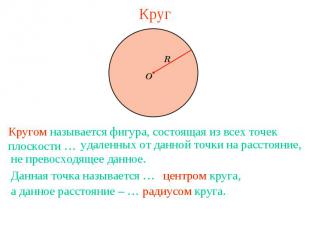
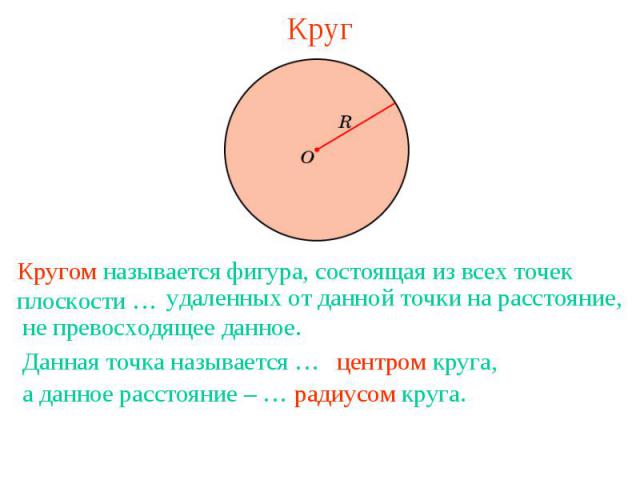
КругКругом называется фигура, состоящая из всех точек плоскости … удаленных от данной точки на расстояние, не превосходящее данное.

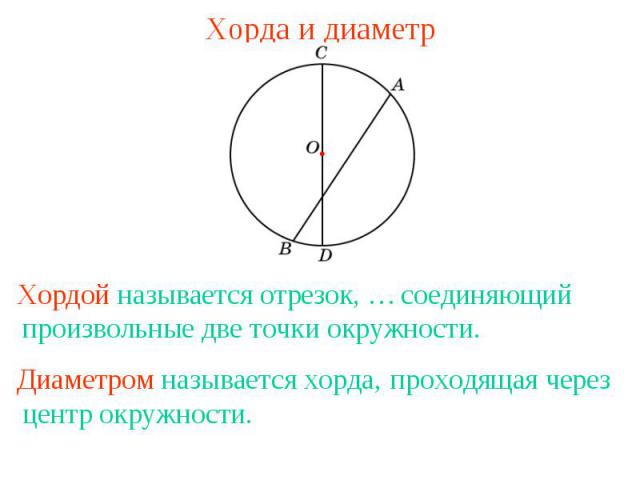
Хорда и диаметр соединяющий произвольные две точки окружности. проходящая через центр окружности.

ТеоремаДиаметр, перпендикулярный хорде, делит эту хорду пополам.Доказательство: Пусть дана окружность с центром в точке О, диаметр АВ перпендикулярен хорде CD. Если хорда CD проходит через центр О, то она является диаметром и делится в точке О пополам. Пусть хорда CD не проходит через центр О. Обозначим точку ее пересечения с диаметром АВ через Е. Треугольники ОЕС и ОЕD равны (по гипотенузе и катету). Следовательно, ЕC = ЕD.

Вопрос 1Какая фигура называется окружностью? Ответ: Окружностью называется фигура, состоящая из всех точек плоскости, удаленных от данной точки на данное расстояние.

Вопрос 2Какая фигура называется кругом? Ответ: Кругом называется фигура, состоящая из всех точек плоскости, удаленных от данной точки на расстояние, не превосходящее данное.

Вопрос 3Что называется: а) хордой; б) диаметром окружности? Ответ: а) Хордой называется отрезок, соединяющий произвольные две точки окружности; б) хорда, проходящая через центр окружности, называется диаметром.

Вопрос 4Чем является наибольшая хорда окружности?

Вопрос 5В каком отношении делит диаметр, перпендикулярную ему хорду?

Упражнение 1Какому неравенству удовлетворяют точки A, лежащие: а) в круге с центром в точке О и радиусом R; б) вне этого круга?

Упражнение 2Сколько диаметров можно провести через центр окружности?

Упражнение 3Сколько окружностей может проходить через две заданные точки?

Упражнение 4Сколько окружностей проходит через три заданные точки, принадлежащие одной прямой?

Упражнение 5Найдите диаметр окружности, если известно, что он на 55 мм больше радиуса.

Упражнение 6Найдите длину наибольшей хорды в окружности, радиус которой равен 5 см.

Упражнение 7Расстояние между точками A и B равно 2 см. Найдите наименьший возможный радиус окружности, проходящей через эти точки.

Упражнение 8Точка A расположена вне окружности радиуса R и удалена от центра O этой окружности на расстояние d. Чему равны наименьшее и наибольшее расстояния от точки A до точек данной окружности?

Упражнение 9Точка A расположена внутри окружности радиуса R и удалена от центра O этой окружности на расстояние d. Чему равны наименьшее и наибольшее расстояния от точки A до точек данной окружности?

Упражнение 10Наибольшее и наименьшее расстояния от данной точки, расположенной вне окружности, до точек окружности равны соответственно 50 см и 20 см. Найдите радиус данной окружности.

Упражнение 11Наибольшее и наименьшее расстояния от данной точки, расположенной внутри окружности, до точек окружности равны соответственно 20 см и 4 см. Найдите радиус данной окружности.

Упражнение 12На рисунке изображена фигура, называемая кольцом. Сформулируйте определение этой фигуры.Ответ: Кольцом называется фигура, состоящая из всех точек плоскости, удаленных от данной точки на расстояние, не превосходящее одного данного расстояния и большее или равное другого данного расстояния.

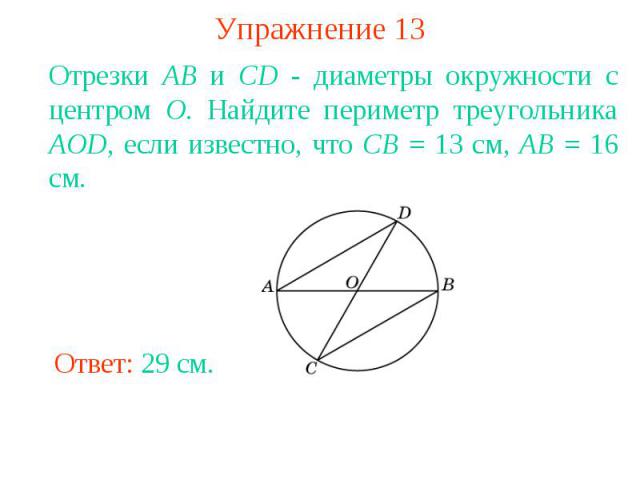
Упражнение 13Отрезки АВ и CD - диаметры окружности с центром О. Найдите периметр треугольника AOD, если известно, что СВ = 13 см, АВ = 16 см.

Упражнение 14Какую фигуру образуют центры окружностей данного радиуса, проходящих через данную точку?

Упражнение 15Какую фигуру образуют центры всех окружностей, проходящих через две данные точки? Ответ: Серединный перпендикуляр к отрезку, соединяющему данные точки.

Упражнение 16Верно ли следующее утверждение: «Равные хорды окружности одинаково удалены от ее центра»? Ответ: Да. Пусть AB = A’B’. Треугольники AOB и A’OB’ равны. Следовательно, равны и их высоты: OH = OH’.

Упражнение 17В окружности на равном расстоянии от центра проведены хорды AB и CD. Чему равна хорда AB, если хорда CD равна 8 см?

Упражнение 18В окружности проведены две равные хорды, одна из которых удалена от центра на 2 см. На каком расстоянии от центра находится другая хорда?

Упражнение 19Найдите внутри окружности точку, через которую можно провести бесконечно много равных хорд.

Упражнение 20Какой длины должны быть две хорды окружности радиуса R, чтобы при любом их положении они пересекались?