Презентация на тему: Каждая сторона треугольника меньше суммы двух других сторон

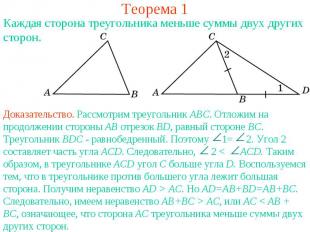
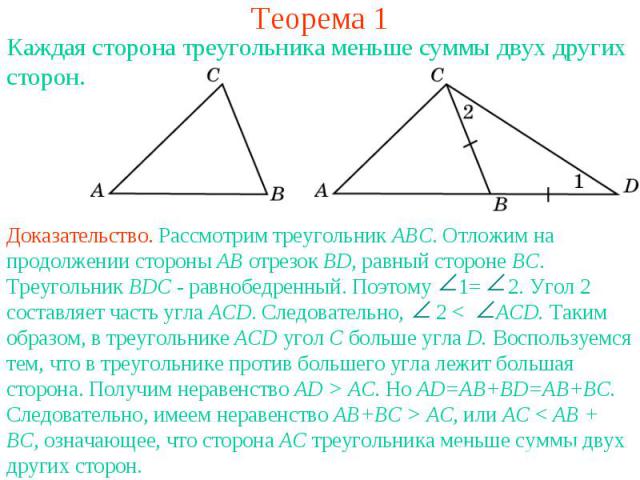
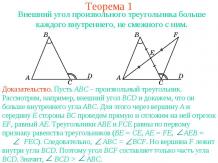
Теорема 1Каждая сторона треугольника меньше суммы двух других сторон.Доказательство. Рассмотрим треугольник АВС. Отложим на продолжении стороны АВ отрезок ВD, равный стороне ВС. Треугольник ВDC - равнобедренный. Поэтому 1= 2. Угол 2 составляет часть угла ACD. Следовательно, 2 < ACD. Таким образом, в треугольнике ACD угол C больше угла D. Воспользуемся тем, что в треугольнике против большего угла лежит большая сторона. Получим неравенство AD > AC. Но AD=AB+BD=AB+BC. Следовательно, имеем неравенство AB+BC > AC, или AC < AB + BC, означающее, что сторона AC треугольника меньше суммы двух других сторон.

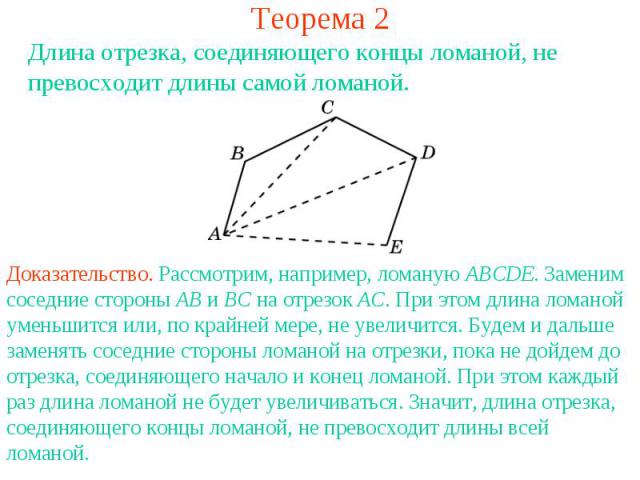
Теорема 2Длина отрезка, соединяющего концы ломаной, не превосходит длины самой ломаной.Доказательство. Рассмотрим, например, ломаную ABCDE. Заменим соседние стороны AB и BC на отрезок AC. При этом длина ломаной уменьшится или, по крайней мере, не увеличится. Будем и дальше заменять соседние стороны ломаной на отрезки, пока не дойдем до отрезка, соединяющего начало и конец ломаной. При этом каждый раз длина ломаной не будет увеличиваться. Значит, длина отрезка, соединяющего концы ломаной, не превосходит длины всей ломаной.

Упражнение 1Можно ли построить треугольник со сторонами: а) 13 см, 2 см, 8 см; б) 1 м, 0,5 м, 0,5 м?

Упражнение 2Могут ли стороны треугольника относится как: а) 1 : 2 : 3; б) 2 : 3 : 6; в) 1 : 1 : 2?

Упражнение 3В равнобедренном треугольнике одна сторона равна 25 см, а другая 10 см. Какая из них является основанием?

Упражнение 4Найдите сторону равнобедренного треугольника, если две другие стороны равны: а) 6 см и 3 см; б) 8 см и 2 см.

Упражнение 5В равнобедренном треугольнике одна сторона равна 12 см, а другая – 5 см. Найдите периметр данного треугольника.

Упражнение 6Периметр равнобедренного треугольника равен 20 см. Одна из сторон больше другой в два раза. Найдите длины сторон этого треугольника.

Упражнение 7Периметр равнобедренного треугольника равен 25 см, разность двух сторон равна 4 см, а один из его внешних углов острый. Найдите стороны треугольника.

Упражнение 8В треугольнике ABC AC = 3,8 см, AB = 0,6 см. Длина стороны BC выражается целым числом. Найдите его.

Упражнение 9В каких пределах может изменяться периметр p треугольника, если две его стороны равны a и b (a < b)?

Упражнение 10Для точек А, В, С, D на плоскости выполняются равенства АВ = 3 см, ВС = 4 см, CD = 5 см и неравенство AC + BD 2 см. Найдите AD.

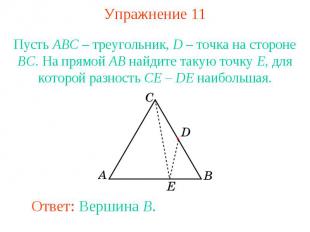
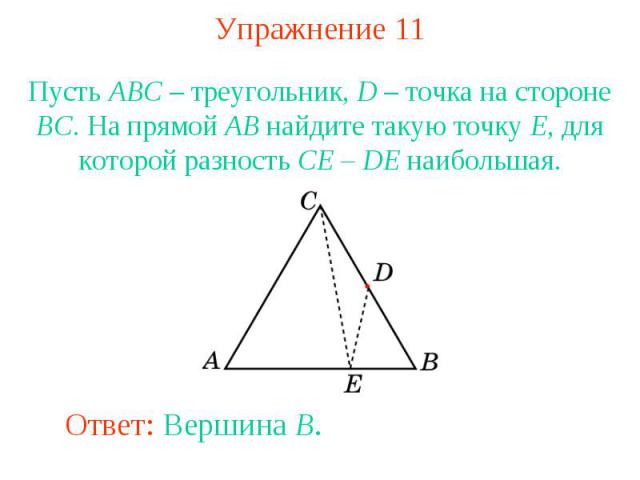
Упражнение 11Пусть ABC – треугольник, D – точка на стороне BC. На прямой AB найдите такую точку E, для которой разность CE – DE наибольшая.

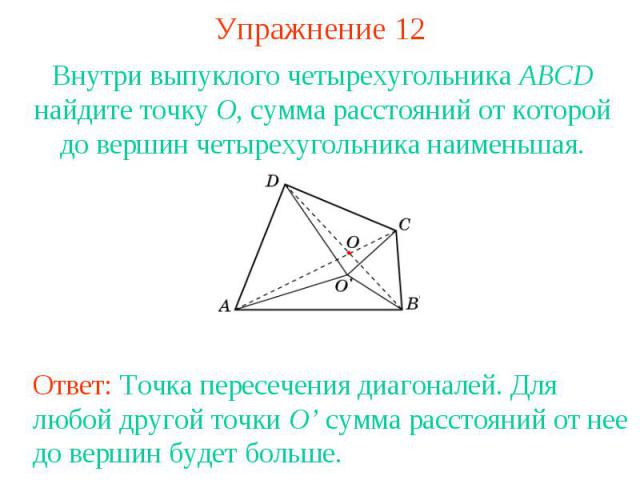
Упражнение 12Внутри выпуклого четырехугольника ABCD найдите точку O, сумма расстояний от которой до вершин четырехугольника наименьшая.Ответ: Точка пересечения диагоналей. Для любой другой точки O’ сумма расстояний от нее до вершин будет больше.

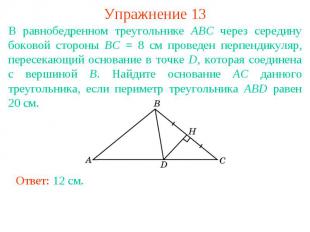
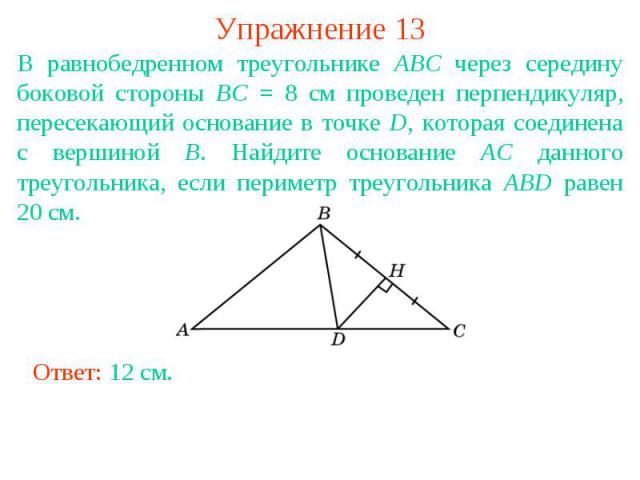
Упражнение 13В равнобедренном треугольнике ABC через середину боковой стороны BC = 8 см проведен перпендикуляр, пересекающий основание в точке D, которая соединена с вершиной B. Найдите основание AC данного треугольника, если периметр треугольника ABD равен 20 см.

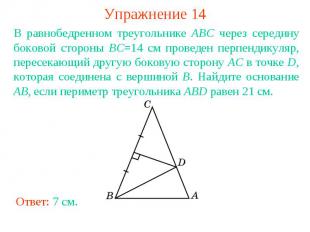
Упражнение 14В равнобедренном треугольнике ABC через середину боковой стороны BC=14 см проведен перпендикуляр, пересекающий другую боковую сторону AC в точке D, которая соединена с вершиной B. Найдите основание AB, если периметр треугольника ABD равен 21 см.

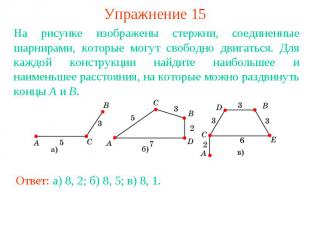
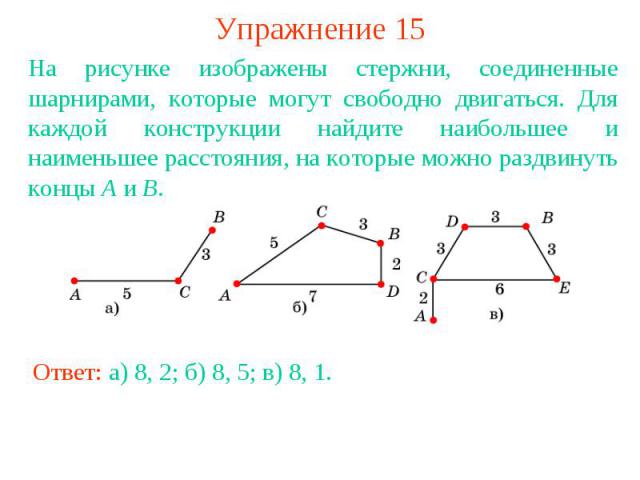
Упражнение 15На рисунке изображены стержни, соединенные шарнирами, которые могут свободно двигаться. Для каждой конструкции найдите наибольшее и наименьшее расстояния, на которые можно раздвинуть концы A и B.