Презентация на тему: Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости

Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости.

Цели урока:Ввести понятие сферы, шара и их элементовВывести уравнение сферы в заданной прямоугольной системе координатРассмотреть возможные случаи взаимного расположения сферы и плоскостиФормировать навык решения задач по теме

ОкружностьОкружность – множество точек плоскости, равноудаленных от данной точкиТочка О – центр окружностиОА - радиус

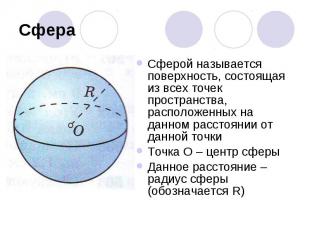
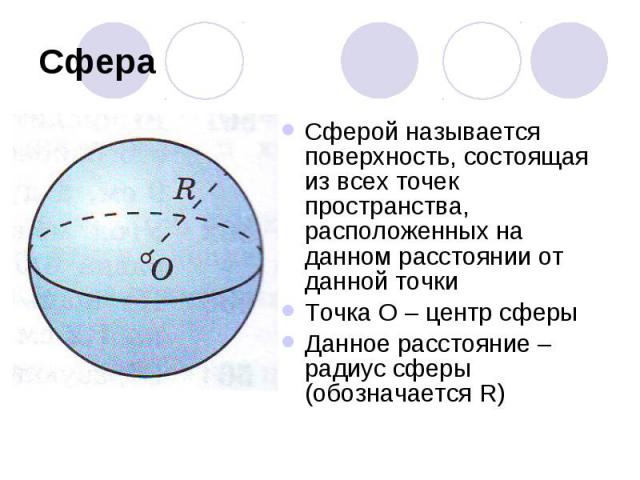
СфераСферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точкиТочка О – центр сферыДанное расстояние – радиус сферы (обозначается R)

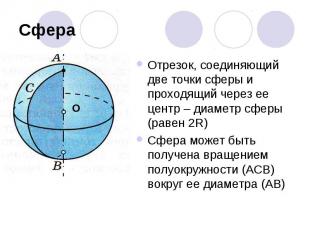
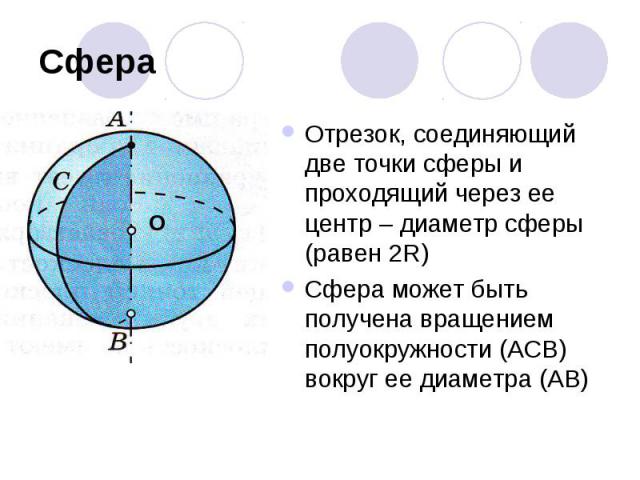
СфераОтрезок, соединяющий две точки сферы и проходящий через ее центр – диаметр сферы (равен 2R)Сфера может быть получена вращением полуокружности (АСВ) вокруг ее диаметра (АВ)

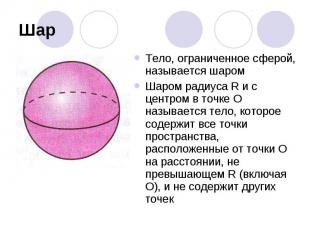
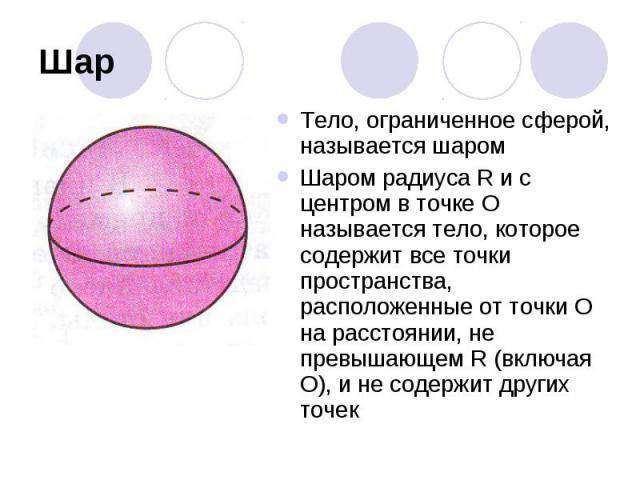
ШарТело, ограниченное сферой, называется шаромШаром радиуса R и с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек

Уравнение сферыПусть R – радиус сферыС(х˳,у˳,z˳) – центр окружностиРасстояние от произвольнойточки М(х,у,z) до точки С найдемпо формулеЕсли точка М лежит на данной сфере, МС = R, или Координаты точки М удовлетворяют уравнению

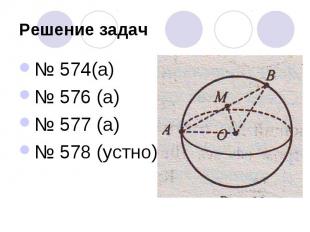
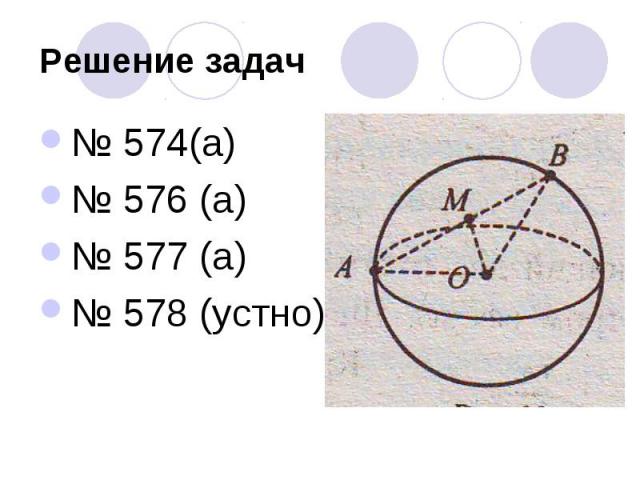
Решение задач№ 574(а)№ 576 (а)№ 577 (а)№ 578 (устно)

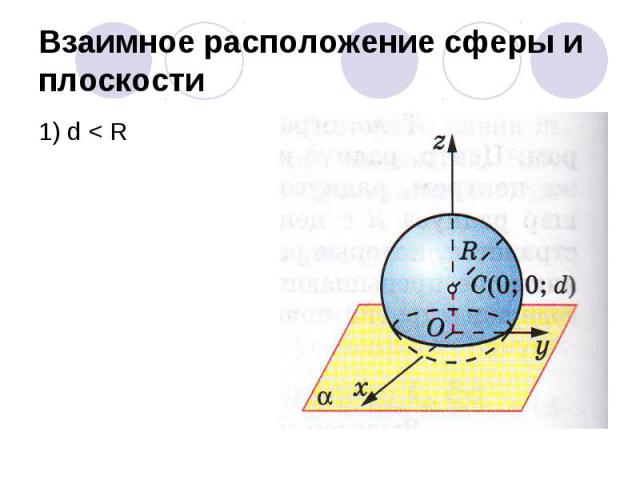
Взаимное расположение сферы и плоскостиОбозначенияR – радиус сферыd – расстояние от центра до плоскости αПлоскость Оху совпадает с плоскостью α, поэтому ее уравнение имеет вид z=0Центр сферы С лежит на положительной полуоси Оz, т.е. имеет координаты С(0;0;d)Уравнение сферы

Взаимное расположение сферы и плоскостиЕсли координаты произвольной точки М (х;у;z) удовлетворяют обоим уравнениям, то М лежит как в плоскости α, так и на сфере.Вопрос о взаимном расположении сводится к исследованию системы уравненийПодставив z = 0 во второе уравнение, получим

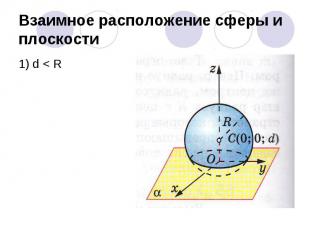
Взаимное расположение сферы и плоскости

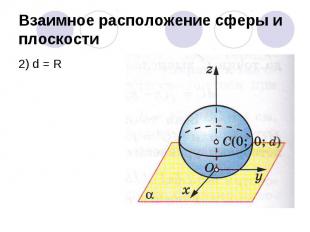
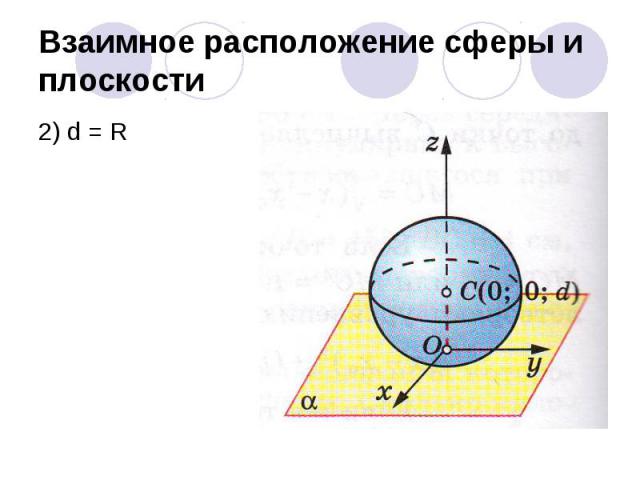
Взаимное расположение сферы и плоскости

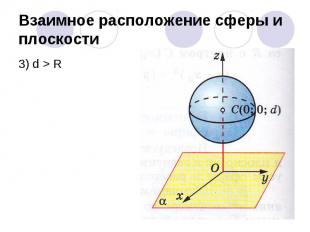
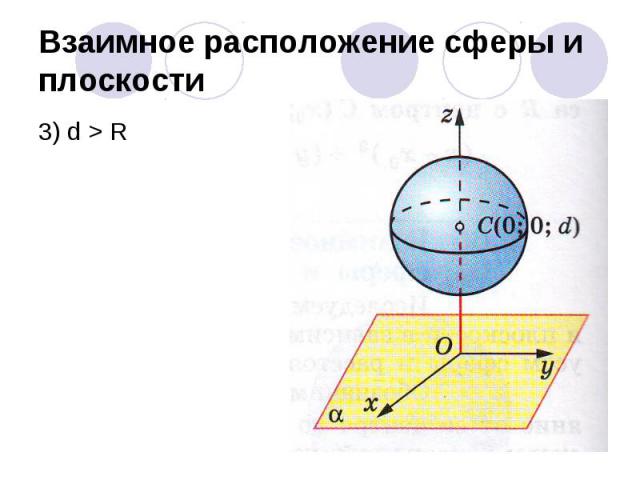
Взаимное расположение сферы и плоскости

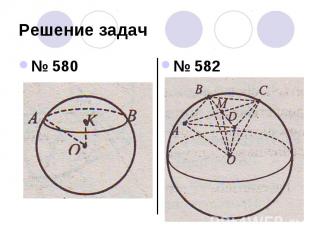
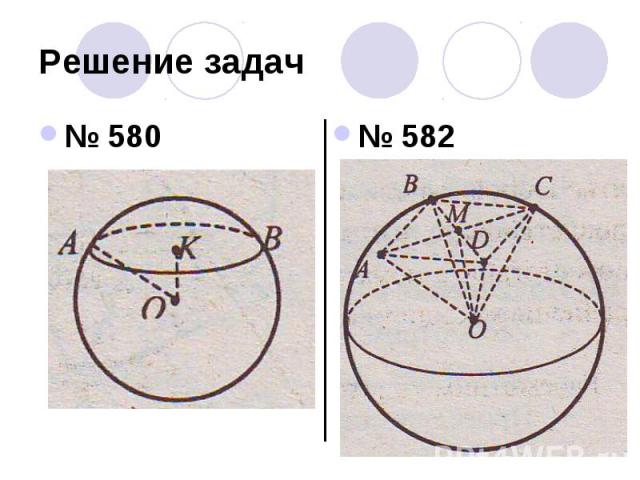
Решение задач

Домашнее заданиеп.64 – 66№ 576 (в)№ 577 (в)№ 581