Презентация на тему: Куб, параллелепипед

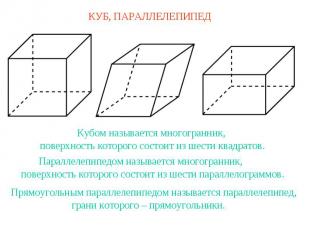
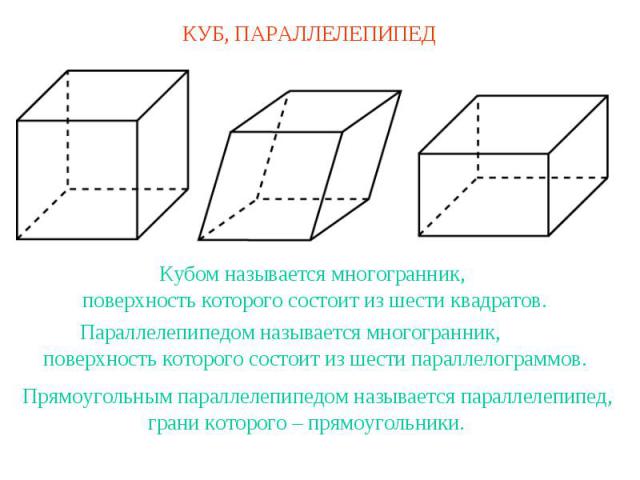
КУБ, ПАРАЛЛЕЛЕПИПЕД Кубом называется многогранник,поверхность которого состоит из шести квадратов.Параллелепипедом называется многогранник,поверхность которого состоит из шести параллелограммов.Прямоугольным параллелепипедом называется параллелепипед,грани которого – прямоугольники.

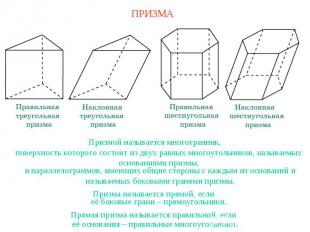
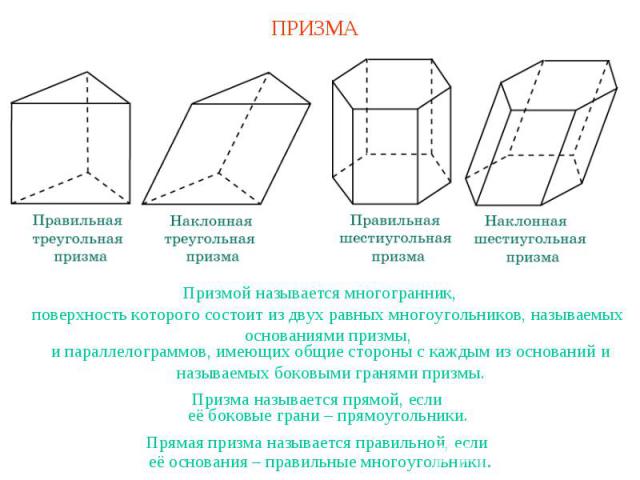
ПРИЗМАПризмой называется многогранник,поверхность которого состоит из двух равных многоугольников, называемых основаниями призмы,и параллелограммов, имеющих общие стороны с каждым из оснований и называемых боковыми гранями призмы.Призма называется прямой, еслиеё боковые грани – прямоугольники.Прямая призма называется правильной, еслиеё основания – правильные многоугольники.

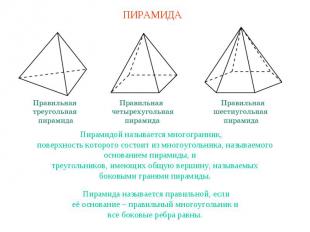
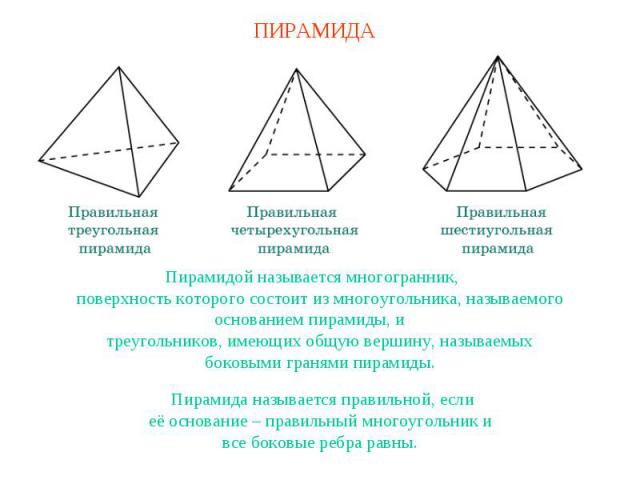
ПИРАМИДАПирамидой называется многогранник,поверхность которого состоит из многоугольника, называемогооснованием пирамиды, итреугольников, имеющих общую вершину, называемыхбоковыми гранями пирамиды.Пирамида называется правильной, еслиеё основание – правильный многоугольник ивсе боковые ребра равны.

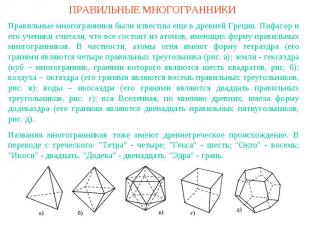
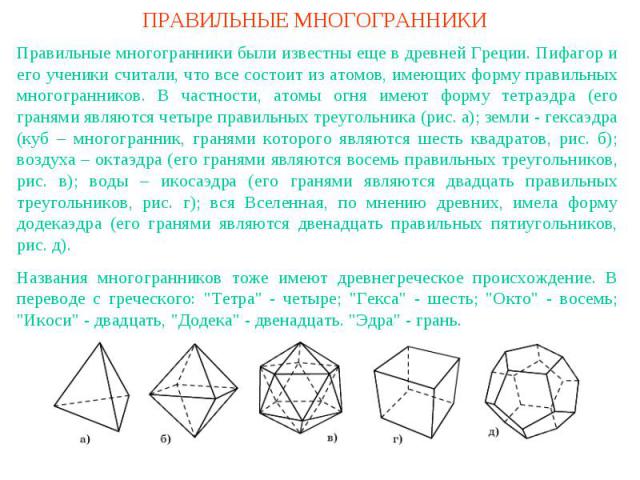
ПРАВИЛЬНЫЕ МНОГОГРАННИКИПравильные многогранники были известны еще в древней Греции. Пифагор и его ученики считали, что все состоит из атомов, имеющих форму правильных многогранников. В частности, атомы огня имеют форму тетраэдра (его гранями являются четыре правильных треугольника (рис. а); земли - гексаэдра (куб – многогранник, гранями которого являются шесть квадратов, рис. б); воздуха – октаэдра (его гранями являются восемь правильных треугольников, рис. в); воды – икосаэдра (его гранями являются двадцать правильных треугольников, рис. г); вся Вселенная, по мнению древних, имела форму додекаэдра (его гранями являются двенадцать правильных пятиугольников, рис. д).Названия многогранников тоже имеют древнегреческое происхождение. В переводе с греческого: "Тетра" - четыре; "Гекса" - шесть; "Окто" - восемь; "Икоси" - двадцать, "Додека" - двенадцать. "Эдра" - грань.

Упражнение 1Существует ли призма, которая имеет:

Упражнение 2Какой многоугольник лежит в основании призмы, которая имеет:

Упражнение 3Существует ли пирамида, которая имеет:

Упражнение 4Какой многоугольник лежит в основании пирамиды, которая имеет:

Упражнение 5Сколько диагоналей у:

Упражнение 6У многогранника шесть вершин и в каждой из них сходится четыре ребра. Сколько у него рёбер?

Упражнение 7У многогранника двенадцать граней и все они пятиугольные. Сколько у него рёбер?

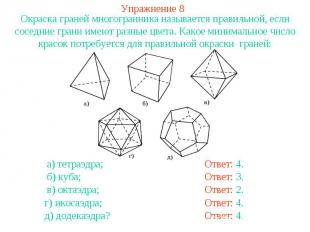
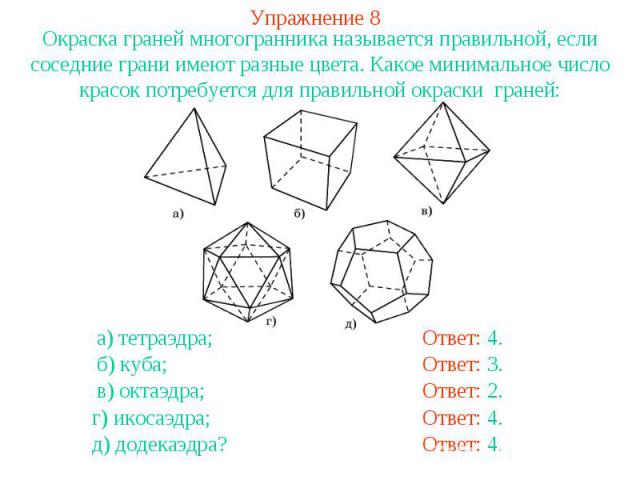
Упражнение 8Окраска граней многогранника называется правильной, если соседние грани имеют разные цвета. Какое минимальное число красок потребуется для правильной окраски граней:

Упражнение 9Сколько рёбер может сходиться в вершине многогранника?Ответ: Любое число, не меньшее 3.

Упражнение 10Найдите сумму всех плоских углов: а) параллелепипеда; б) тетраэдра; в) четырёхугольной пирамиды.

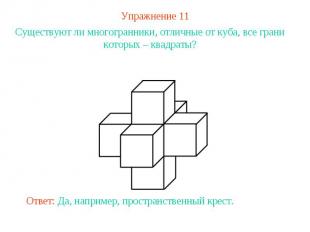
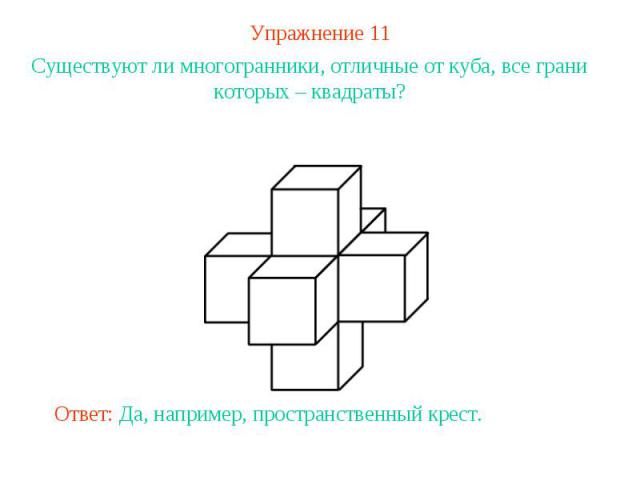
Упражнение 11Существуют ли многогранники, отличные от куба, все грани которых – квадраты?Ответ: Да, например, пространственный крест.

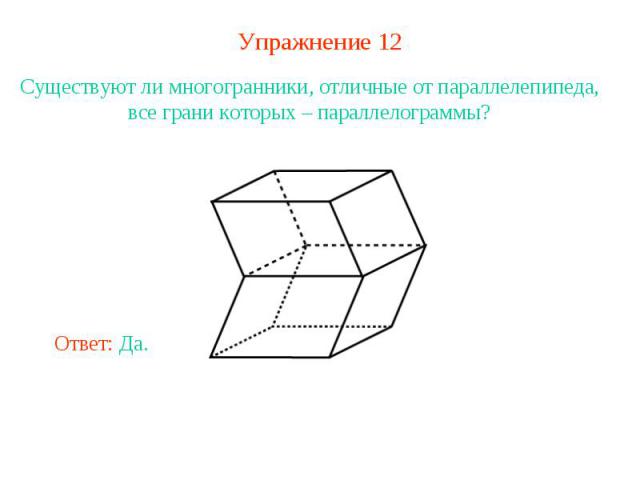
Упражнение 12Существуют ли многогранники, отличные от параллелепипеда, все грани которых – параллелограммы?