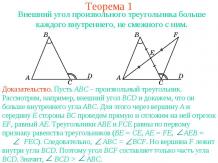
Презентация на тему: Параллельное проектирование

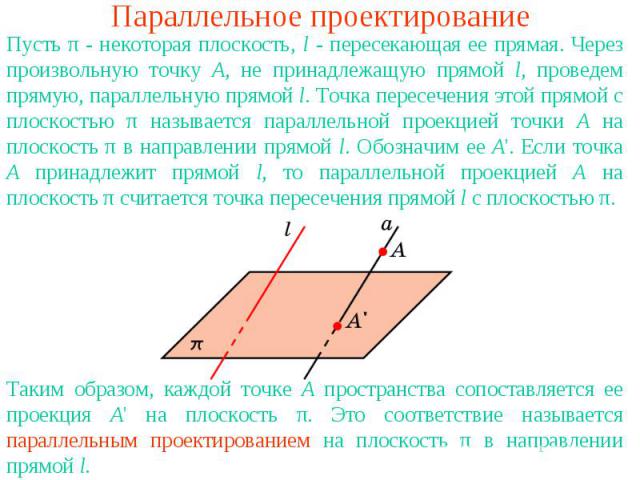
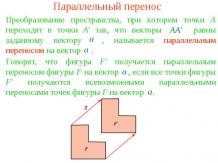
Параллельное проектированиеПусть π - некоторая плоскость, l - пересекающая ее прямая. Через произвольную точку A, не принадлежащую прямой l, проведем прямую, параллельную прямой l. Точка пересечения этой прямой с плоскостью π называется параллельной проекцией точки A на плоскость π в направлении прямой l. Обозначим ее A'. Если точка A принадлежит прямой l, то параллельной проекцией A на плоскость π считается точка пересечения прямой l с плоскостью π.Таким образом, каждой точке A пространства сопоставляется ее проекция A' на плоскость π. Это соответствие называется параллельным проектированием на плоскость π в направлении прямой l.

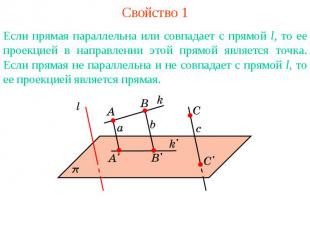
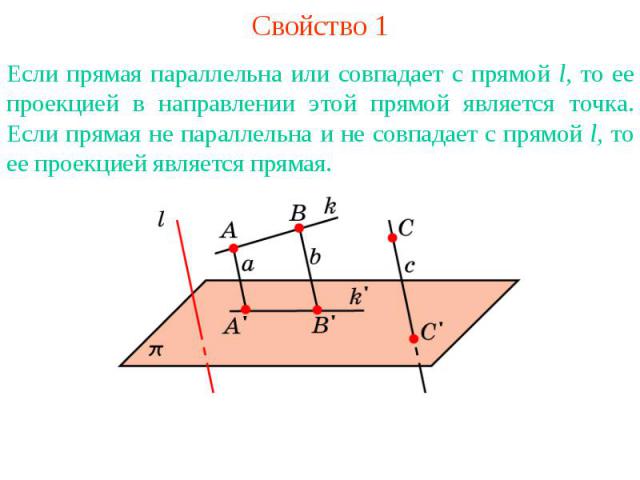
Свойство 1Если прямая параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.

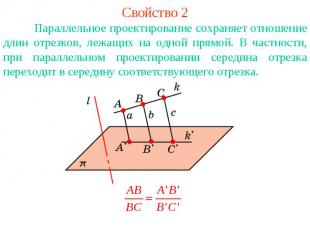
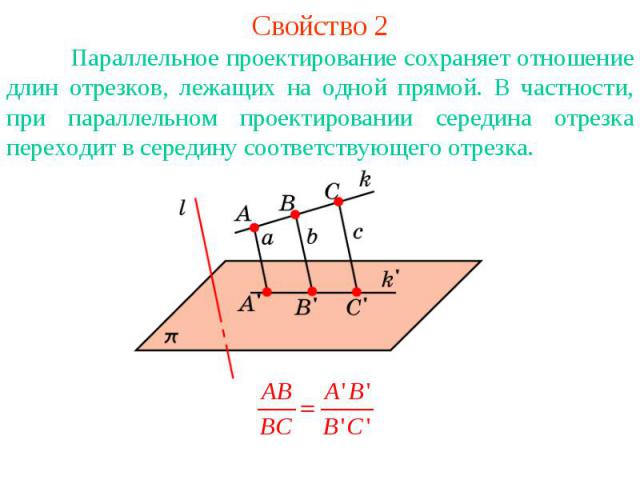
Свойство 2Параллельное проектирование сохраняет отношение длин отрезков, лежащих на одной прямой. В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.

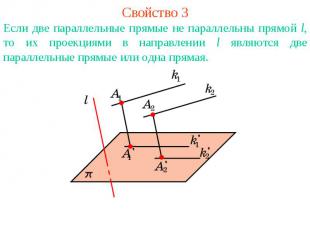
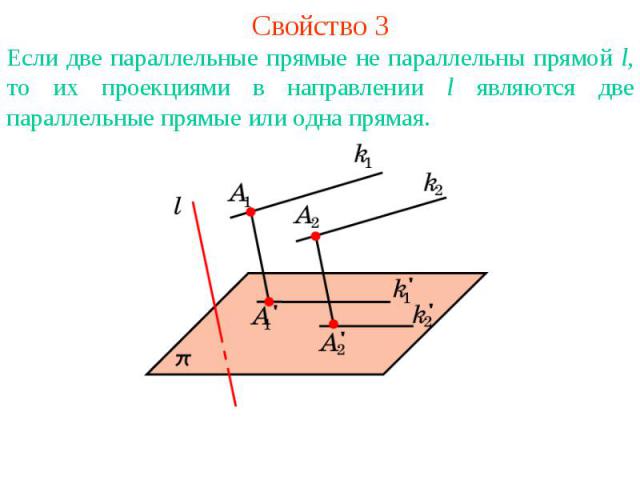
Свойство 3Если две параллельные прямые не параллельны прямой l, то их проекциями в направлении l являются две параллельные прямые или одна прямая.

Упражнение 1В каком случае параллельной проекцией прямой будет точка? Ответ: Если прямая параллельна направлению проектирования.

Упражнение 2Сколько точек может получиться при параллельном проектировании трех различных точек пространства?

Упражнение 3Какие фигуры могут служить параллельными проекциями двух пересекающихся прямых? Ответ: Две пересекающиеся прямые или одна прямая.

Упражнение 4В каком случае параллельной проекцией двух параллельных прямых является одна прямая? Ответ: Если они лежат в плоскости, параллельной направлению проектирования, но не параллельны ему.

Упражнение 5В каком случае параллельной проекцией двух параллельных прямых являются две точки? Ответ: Если они параллельны направлению проектирования.

Упражнение 6Какие фигуры могут быть параллельными проекциями двух скрещивающихся прямых? Ответ: Пересекающиеся прямые, параллельные прямые, прямая и точка.

Упражнение 7Как должны быть расположены прямая и точка, чтобы они проектировались на плоскость в прямую и точку, принадлежащую этой прямой? Ответ: Прямая не параллельна направлению проектирования, и через эту прямую и данную точку проходит плоскость, параллельная направлению проектирования.

Упражнение 8Как должны быть расположены две прямые, чтобы они проектировались на плоскость в прямую и точку, принадлежащую этой прямой? Ответ: Пересекаться и одна из них параллельна направлению проектирования.

Упражнение 9Как должны быть расположены две прямые, чтобы они проектировались на плоскость в прямую и точку, не принадлежащую этой прямой? Ответ: Скрещиваться и одна из них параллельна направлению проектирования.

Упражнение 10Сохраняются ли при параллельном проектировании величины углов?

Упражнение 11Сохраняются ли при параллельном проектировании длины отрезков?

Упражнение 12Может ли параллельная проекция угла быть больше (меньше) самого угла?

Упражнение 13Может ли параллельная проекция отрезка быть больше (меньше) самого отрезка?

Упражнение 14Верно ли, что если длина отрезка равна длине его параллельной проекции, то отрезок параллелен плоскости проектирования?

Упражнение 15Точки A’, B’ являются параллельными проекциями точек A, B. AA’ = a, BB’ = b. Точка C делит отрезок AB в отношении m : n. Найдите расстояние между точкой C и ее проекцией C’.