Презентация на тему: Параллельное программирование

Параллельное программирование Минакова Е.О.Студентка 6 курса ОНУ им.И.И.Мечникова

Что же такое параллельное программирование Представьте себе такую картину: несколько автомобилей едут из пункта А в пункт В. Машины могут бороться за дорожное пространство и либо следуют в колонне, либо обгоняют друг друга (попадая при этом в аварии!). Они могут также ехать по параллельным полосам дороги и прибыть почти одновременно, не "переезжая" дорогу друг другу. Возможен вариант, когда все машины поедут разными маршрутами и по разным дорогам. Эта картина и демонстрирует суть параллельных вычислений.

Что же нужно, чтобы достичь параллелизма? Достижение параллелизма возможно только при выполнимости следующихтребований к архитектурным принципам построения вычислительной системы:независимость функционирования отдельных устройств ЭВМ - данное требование относится в равной степени ко всем основным компонентам вычислительной системы - к устройствам ввода-вывода, к обрабатывающим процессорам и к устройствам памяти; избыточность элементов вычислительной системы - организация избыточности может осуществляться в следующих основных формах: использование специализированных устройств таких, например, как отдельных процессоров для целочисленной и вещественной арифметики, устройств многоуровневой памяти (регистры, кэш); дублирование устройств ЭВМ путем использования, например, нескольких однотипных обрабатывающих процессоров или нескольких устройств оперативной памяти.

Примеры топологий многопроцессорных вычислительных систем полный граф (completely-connected graph or clique)- система, в которой между любой парой процессоров существует прямая линия связи; как результат, данная топология обеспечивает минимальные затраты при передаче данных, однако является сложно реализуемой при большом количестве процессоров; линейка (linear array or farm) - система, в которой каждый процессор имеет линии связи только с двумя соседними (с предыдущим и последующим) процессорами; такая схема является, с одной стороны, просто реализуемой, а с другой стороны, соответствует структуре передачи данных при решении многих вычислительных задач (например, при организации конвейерных вычислений);

Примеры топологий многопроцессорных вычислительных систем кольцо (ring) - данная топология получается из линейки процессоров соединением первого и последнего процессоров линейки; звезда (star) - система, в которой все процессоры имеют линии связи с некоторым управляющим процессором; данная топология является эффективной, например, при организации централизованных схем параллельных вычислений;

Примеры топологий многопроцессорных вычислительных систем решетка (mesh) - система, в которой граф линий связи образует прямоугольную сетку (обычно двух- или трех- мерную); подобная топология может быть достаточно просто реализована и, кроме того, может быть эффективно используема при параллельном выполнении многих численных алгоритмов (например, при реализации методов анализа математических моделей, описываемых дифференциальными уравнениями в частных производных); гиперкуб (hypercube) - данная топология представляет частный случай структуры решетки, когда по каждой размерности сетки имеется только два процессора (т.е. гиперкуб содержит 2N процессоров при размерности N);

КЛАССЫ ЗАДАЧ, КОТОРЫЕ МОЖНО ЭФФЕКТИВНО РАСПАРАЛЛЕЛИТЬ Одномерные массивыДвумерные массивыКлеточные автоматыСистемы дифференциальных уравнений

ВЫЧИСЛЕНИЕ ЧАСТНЫХ СУММ ПОСЛЕДОВАТЕЛЬНОСТИ ЧИСЛОВЫХ ЗНАЧЕНИЙ Последовательный алгоритм суммированияТрадиционный алгоритм для решения этой задачи состоит впоследовательном суммировании элементов числовогонабораВычислительная схема данного алгоритма может бытьпредставлена следующим образом (Рис.1). Каскадная схема суммированияПараллелизм алгоритма суммирования становится возможным только при ином способе построения процесса вычислений, основанном на использовании ассоциативности операции сложения. Получаемый новый вариант суммирования (известный в литературе как каскадная схема) состоит в следующем:на первой итерации каскадной схемы все исходные данные разбиваются на пары и для каждой пары вычисляется сумма значений, далее все полученные суммы пар также разбиваются на пары и снова выполняется суммирование значений пар и т.д. (Рис.2).

Что все это значит Модифицированная каскадная схемаПолучение асимптотически ненулевой эффективности может быть обеспечено, например, прииспользовании модифицированной каскадной схемы. В новом варианте каскадной схемы всепроводимые вычисления подразделяется на два последовательно выполняемых этапа суммирования (см. Рис. 3): на первом этапе вычислений все суммируемые значения подразделяются на  групп, в каждой из которых содержится   элементов; далее для каждой группы вычисляется сумма значений при помощи последовательного алгоритма суммирования; вычисления в каждой группе могут выполняться независимо друг от друга (т.е. параллельно – для этого необходимо наличие не менее  процессоров); на втором этапе для полученных  сумм отдельных групп применяется обычная каскадная схема.

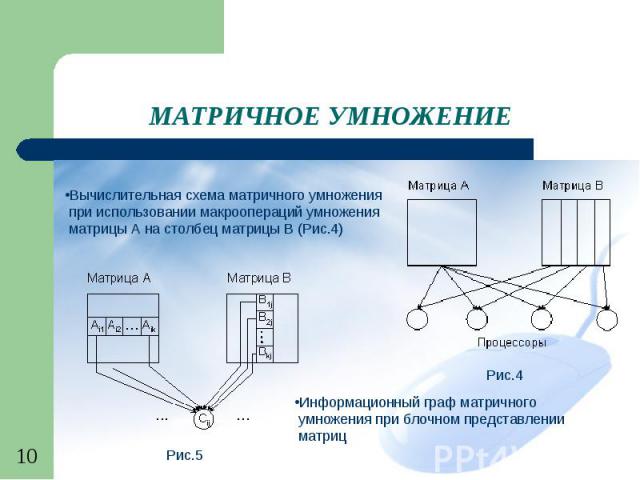
МАТРИЧНОЕ УМНОЖЕНИЕ Вычислительная схема матричного умножения при использовании макроопераций умножения матрицы A на столбец матрицы B (Рис.4) Информационный граф матричного умножения при блочном представлении матриц

МАТРИЧНОЕ УМНОЖЕНИЕСостояние блоков на каждом процессоре в ходе выполнения итераций этапа вычислений

Таким образом, тема увеличения скорости вычислений весьма актуальна для всех тех, чья деятельность связана с большим объемом вычислительных работ. А так как чаще всего средств для закупки мощных компьютеров типа nCube, Cray или подобных им нет, поэтому развитие программного обеспечения и появление свободно распространяемой операционной системы Linux позволило создать вычислительный комплекс с эффективным быстродействием, сравнимым с быстродействием суперкомпьютеров, но со стоимостью в десятки раз меньшей.