Презентация на тему: Алгоритмы и структурное програмирование

Понятие и свойства алгоритмаЯзык блок-схемПростая программа, cтруктурный подход к разработке алгоритмовОсновные структуры алгоритмовЯзык проектирования программ (псевдокод)Рекурсивные алгоритмыАлгоритмы поискаАлгоритмы сортировкиПринципы объектно-ориентированного программирования

Алгоритм - формальное описание последовательности действий, которое необходимо выполнить для решения задачи. Гл. 4. АЛГОРИТМЫ И СТРУКТУРНОЕ ПРОГРАММИРОВАНИЕ Дискретность. Алгоритм представляет процесс решения задачи как последовательность выполнения шагов-этапов. Для выполнения каждого эпата требуется определенное время, т.е. преобразование исходных данных в результат происходит дискретно во времени.Определенность (детерминированность). Каждое правило алгоритма должно быть четким и однозначным. Отсюда выполнение алгоритма носит механический характер. Результативность (финитность, конечность). Алгоритм должен приводить к решению задачи за конечное число шагов. Массовость. Алгоритм решения задачи разрабатывается в общем виде, т.е. он должен быть применим для некоторого класса задач, различающихся исходными данными (область применимости алгоритма).

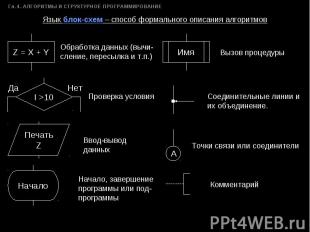
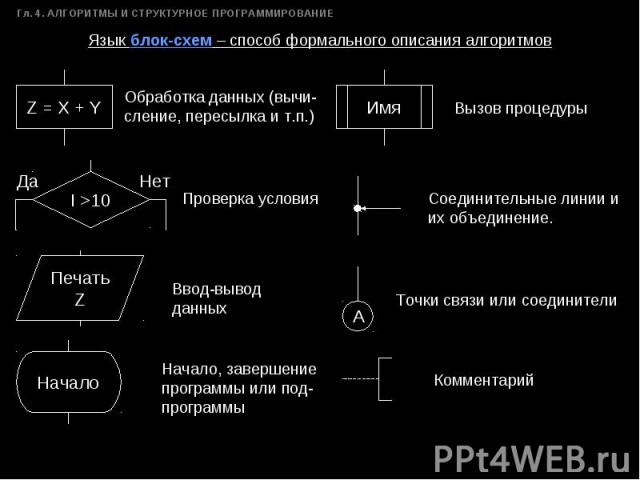
Язык блок-схем – способ формального описания алгоритмов Обработка данных (вычи-сление, пересылка и т.п.) Проверка условия Ввод-вывод данных Начало, завершение программы или под-программы Вызов процедуры Соединительные линии и их объединение. Точки связи или соединители

Основные (базовые) структуры алгоритмов – это ограниченный набор стандартных способов соединения отдельных блоков или структур блоков для выполнения типичных последовательностей действий. Доказано, что программу для любой простой логической задачи можно составить из структур следование, разветвление и повторение (цикл). Эти базовые структуры были положены в основу технологии структурного программирования. Эта технология для разработки сложных программ рекомендует разбивать (декомпозировать) программу на подпрограммы (процедуры), решающие отдельные подзадачи, т.е. базируется на процедурной декомпозиции. Простая программа - алгоритм, для которого:Существует единственный вход и единственный выход.Для каждого элемента алгоритма существует путь от входа к выходу через этот элемент (т.е. алгоритм не содержит бесконечных циклов и не содержит бесполезных (недостижимых) фрагментов).

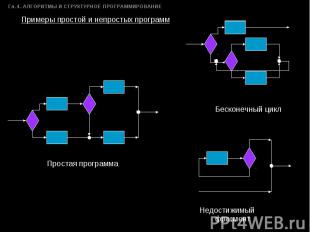
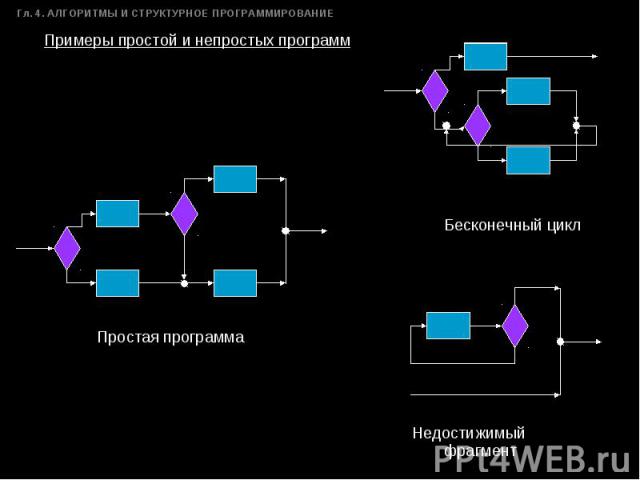
Примеры простой и непростых программ Простая программа Бесконечный цикл Недостижимый фрагмент

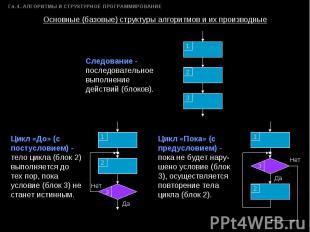
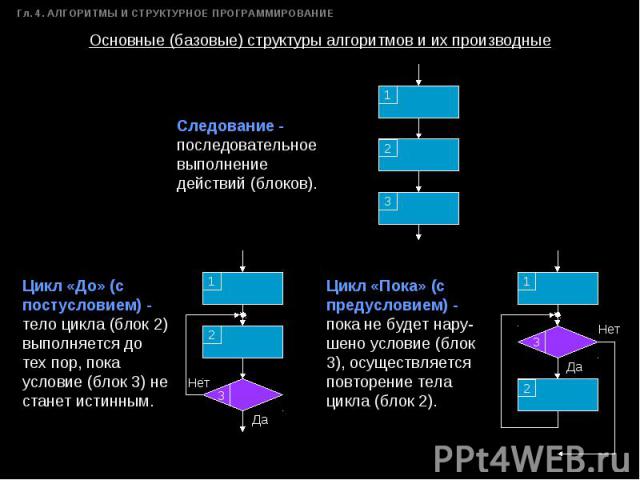
Основные (базовые) структуры алгоритмов и их производные Следование -последовательное выполнение действий (блоков). Цикл «До» (с постусловием) -тело цикла (блок 2) выполняется до тех пор, пока условие (блок 3) не станет истинным. Цикл «Пока» (с предусловием) - пока не будет нару-шено условие (блок 3), осуществляется повторение тела цикла (блок 2).

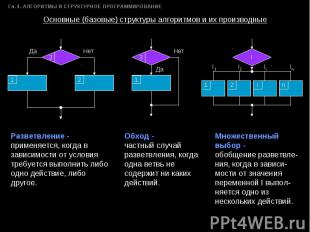
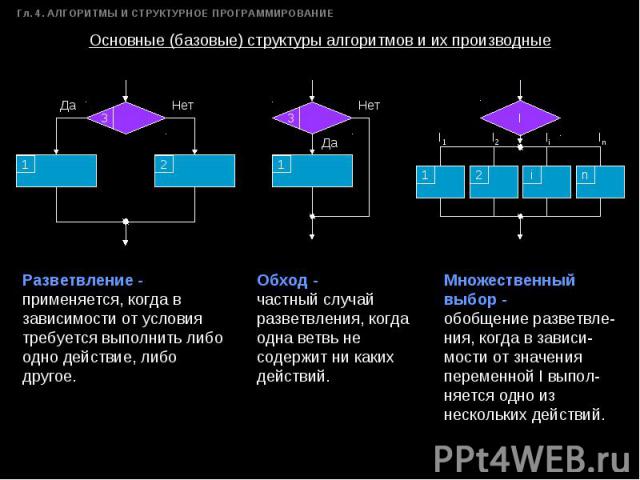
Основные (базовые) структуры алгоритмов и их производные Разветвление - применяется, когда в зависимости от условия требуется выполнить либо одно действие, либо другое. Обход - частный случай разветвления, когда одна ветвь не содержит ни каких действий. Множественный выбор - обобщение разветвле-ния, когда в зависи-мости от значения переменной I выпол-няется одно из нескольких действий.

Альтернативный способ описания логики программы на этапе проектирования – использование псевдокода (или языка проектирования программ PDL – Process Design Language). Он занимает промежуточное положение между естественным языком и языком программирования и состоит из внешнего синтаксиса и внутреннего синтаксиса.Внешний синтаксис – заданный набор операторов, построенных по образцу языков программирования и описывающий логику программы. Внешний синтаксис соответствует основным структурам алгоритмов. Кроме того, к внешнему синтаксису также относятся процедуры и модули. Процедура – это хранимые в памяти машины подпрограммы, которые могут вызываться для выполнения из различных мест основной программы, либо из других процедур. Она вызывается и выполняется до завершения без сохранения внутренних данных. Модуль – это несколько процедур, организованных в систему для удобства работы пользователя. Модуль имеет доступ к общим данным, которые сохраняются между последовательными вызовами модуля. Внутренний синтаксис – общий, обычно специально не определяемый синтаксис, пригодный для описания задач в данной области. Практически любое предложение, написанное на естественном языке, либо на специализированном языке (например, математические формулы) может быть использовано.

Следование. Записываются последовательно операции одна под другой. Для отделения части последовательности операторов используются операторы – do…end-do. Индексная последовательность (цикл по счетчику). Цикл с заранее определенным числом шагов (среднее между обычными последовательностью и классическим циклом). Цикл-До. Операции структуры, включая модификацию until-теста, выполняются один или более раз до тех пор, пока until-тест не примет значение истина; первая операциявторая операцияdo третья операцияend-do for индексный списокdo do-частьend-do do do-частьuntil until-тестend-do

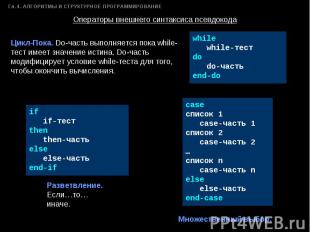
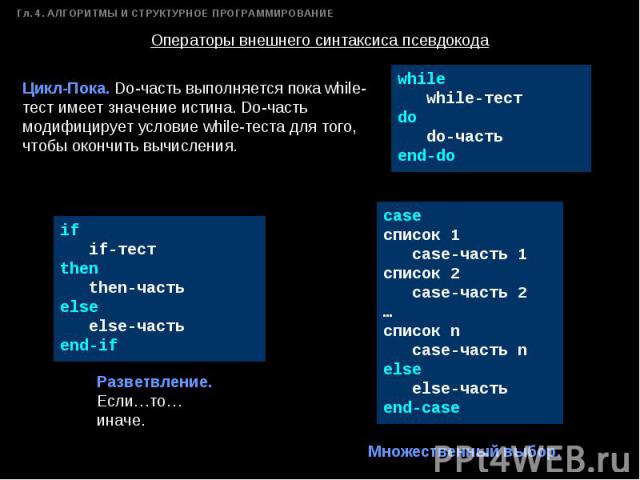
Цикл-Пока. Do-часть выполняется пока while-тест имеет значение истина. Do-часть модифицирует условие while-теста для того, чтобы окончить вычисления. if if-тестthen then-частьelse else-частьend-if Разветвление. Если…то…иначе. while while-тестdo do-частьend-do caseсписок 1 case-часть 1список 2 case-часть 2…список n case-часть nelse else-частьend-case

Алгоритмы вычисления суммы квадратов первых N целых чисел с использованием псевдокода и языка блок-схем Ввести Число слагаемыхСумма = 0Номер = 1do Сумма = Сумма + Номер2 Увеличить Номер на единицуuntil Номер > Число слагаемыхend-doНапечатать Сумму

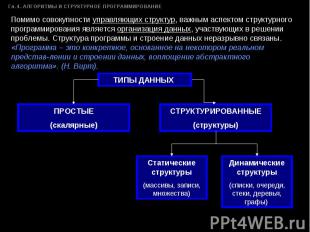
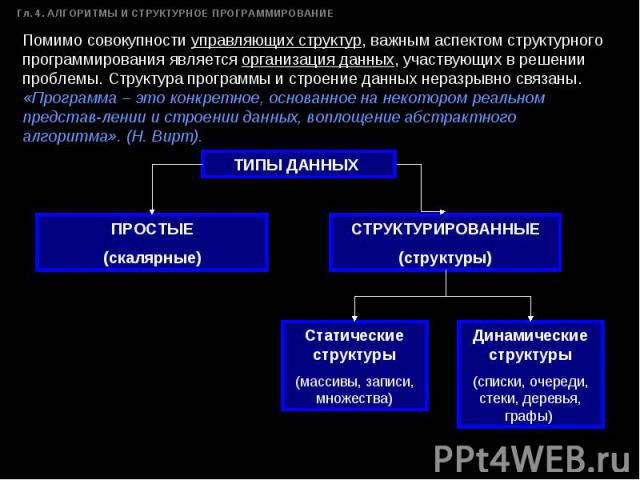
Помимо совокупности управляющих структур, важным аспектом структурного программирования является организация данных, участвующих в решении проблемы. Структура программы и строение данных неразрывно связаны. «Программа – это конкретное, основанное на некотором реальном представ-лении и строении данных, воплощение абстрактного алгоритма». (Н. Вирт).

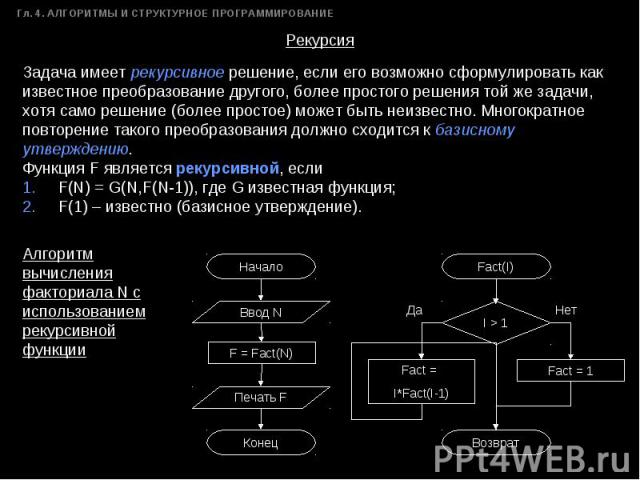
Задача имеет рекурсивное решение, если его возможно сформулировать как известное преобразование другого, более простого решения той же задачи, хотя само решение (более простое) может быть неизвестно. Многократное повторение такого преобразования должно сходится к базисному утверждению. Функция F является рекурсивной, если1.     F(N) = G(N,F(N-1)), где G известная функция;2.     F(1) – известно (базисное утверждение). Алгоритм вычисления факториала N с использованием рекурсивной функции

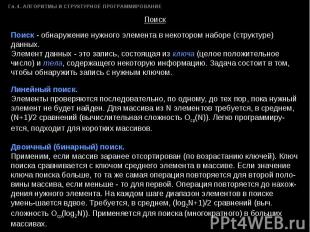
Поиск - обнаружение нужного элемента в некотором наборе (структуре) данных. Элемент данных - это запись, состоящая из ключа (целое положительное число) и тела, содержащего некоторую информацию. Задача состоит в том, чтобы обнаружить запись с нужным ключом. Линейный поиск.Элементы проверяются последовательно, по одному, до тех пор, пока нужный элемент не будет найден. Для массива из N элементов требуется, в среднем, (N+1)/2 сравнений (вычислительная сложность Оср(N)). Легко программиру-ется, подходит для коротких массивов. Двоичный (бинарный) поиск.Применим, если массив заранее отсортирован (по возрастанию ключей). Ключ поиска сравнивается с ключом среднего элемента в массиве. Если значение ключа поиска больше, то та же самая операция повторяется для второй поло-вины массива, если меньше - то для первой. Операция повторяется до нахож-дения нужного элемента. На каждом шаге диапазон элементов в поиске умень-шается вдвое. Требуется, в среднем, (log2N+1)/2 сравнений (выч. сложность Оср(log2N)). Применяется для поиска (многократного) в больших массивах.

Сортировка (упорядочение) - переразмещение элементов данных в возрастающем или убывающем порядке. При выборе метода сортировки необходимо учитывать число сортируемых элементов (N) и до какой степени элементы уже отсортированы. Критерии оценки метода сортировки:- количество необходимых операций сравнения в зависимости от числа элементов N, вычислительная сложность алгоритма характеризуется с помощью О-функции, аргументом которой является другая функция от N;- эффективность использования памяти где S(N) - объем памяти, занимаемый элементами данных до сортировки, S(N) - объем дополнительной памяти, требуемой в процессе сортировки.

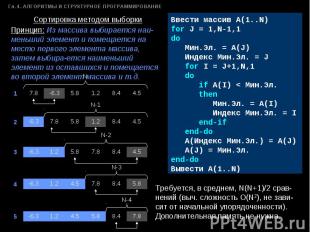
Сортировка методом выборки Принцип: Из массива выбирается наи-меньший элемент и помещается на место первого элемента массива, затем выбира-ется наименьший элемент из оставшихся и помещается во второй элемент массива и т.д. Ввести массив A(1..N)for J = 1,N-1,1do Мин.Эл. = А(J) Индекс Мин.Эл. = J for I = J+1,N,1 do if A(I) < Мин.Эл. then Мин.Эл. = A(I) Индекс Мин.Эл. = I end-if end-do A(Индекс Мин.Эл.) = A(J) A(J) = Мин.Эл.end-doВывести A(1..N) Требуется, в среднем, N(N+1)/2 срав-нений (выч. сложность O(N2), не зави-сит от начальной упорядоченности). Дополнительная память не нужна.

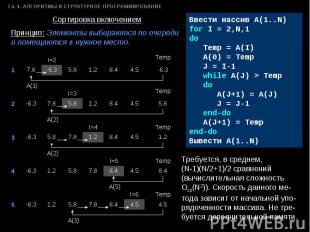
Принцип: Элементы выбираются по очереди и помещаются в нужное место. Ввести массив A(1..N)for I = 2,N,1do Temp = А(I) A(0) = Temp J = I-1 while A(J) > Temp do A(J+1) = A(J) J = J-1 end-do A(J+1) = Tempend-doВывести A(1..N) Требуется, в среднем, (N-1)(N/2+1)/2 сравнений (вычислительная сложность Оср(N2)). Скорость данного ме-тода зависит от начальной упо-рядоченности массива. Не тре-буется дополнительной памяти.

Принцип: Выбираются два элемента, и если друг по отношению к другу они не находятся нужном порядке, то меня-ются местами. Процесс продолжается пока никакие два элемента не нужно менять местами. Ввести массив A(1..N)K = 1, I = 1 while K <> 0do K = 0 for J = 1,N-I,1 do if A(J) > A(J+1) then T = A(J), A(J) = A(J+1), A(J+1) = T, K = K+1 end-if end-do I = I +1end-doВывести A(1..N) Вычислительная сложность данного метода сильно зависит от исходного расположения элементов. Минимальное значение числа сравнений – N-1 в полностью отсортированном массиве, максимальное – (N2-N)/2 при начальной сортировке в обратном порядке. Средняя вычислительная сложность Оср(N2). Доп. память не требуется.

Принцип: Элементы массива рассматриваются как совокупность цифр (символов), первый шаг - сортировка по значению старшей цифры, затем полученные подмножества (группы) сортируются по значению следующей цифры и т.д. Каждый элемент массива А (1..N) - совокупность цифр С1С2С3…Сm, где m - количество цифр максимального элемента (если какой-то элемент содержит меньше цифр, то он слева дополняется нулями). Средняя вычислительная сложность Оср(N log2N) и лучше, если m (число цифр) мало. Требуется дополнительный массив размером N, и еще массив размером 10, в котором подсчитывается число элементов с выделяемой цифрой 0,1,…9.

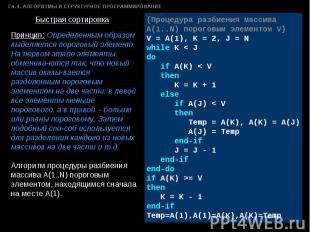
Принцип: Определенным образом выделяется пороговый элемент. На первом этапе элементы обменива-ются так, что новый массив оказы-вается разделенным пороговым элементом на две части: в левой все элементы меньше порогового, а в правой – больше или равны пороговому. Затем подобный спо-соб используется для разделения каждого из новых массивов на две части и т.д. Алгоритм процедуры разбиения массива А(1..N) пороговым элементом, находящимся сначала на месте А(1). {Процедура разбиения массива A(1..N) пороговым элементом V}V = A(1), K = 2, J = Nwhile K < Jdo if A(K) < V then K = K + 1 else if A(J) < V then Temp = A(K), A(K) = A(J) A(J) = Temp end-if J = J - 1 end-ifend-doif A(K) >= Vthen K = K - 1end-ifTemp=A(1),A(1)=A(K),A(K)=Temp

Средняя вычислительная сложность - Оср(N log2N). Важное значение имеет выбор значения порогового элемента. В частности, если исходный массив близок к отсортированному, то при выборе пороговым элементом первого элемента (как в примере) вычислительная сложность алгоритма будет О(N2). Желательно, чтобы пороговый элемент в конечном итоге разделил массив приблизительно на две равные части.

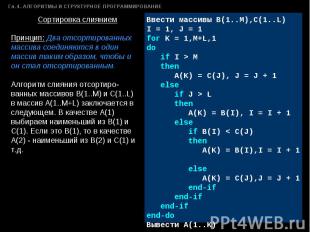
Принцип: Два отсортированных массива соединяются в один массив таким образом, чтобы и он стал отсортированным. Алгоритм слияния отсортиро-ванных массивов B(1..M) и C(1..L) в массив A(1..M+L) заключается в следующем. В качестве А(1) выбираем наименьший из В(1) и С(1). Если это В(1), то в качестве А(2) - наименьший из В(2) и С(1) и т.д. Ввести массивы B(1..M),С(1..L)I = 1, J = 1for K = 1,M+L,1do if I > M then A(K) = C(J), J = J + 1 else if J > L then A(K) = B(I), I = I + 1 else if B(I) < C(J) then A(K) = B(I),I = I + 1 else A(K) = C(J),J = J + 1 end-if end-if end-ifend-doВывести A(1..K)

Сортировка слиянием Если имеется один неотсортированный массив А(1..N), то его можно рассматривать как совокупность N отсортированных массивов, каждый из которых состоит из одного элемента.Первый шаг - слияние массивов попарно, затем объединение пар в четверки и т.д.Cредняя вычислительная сложность алгоритма - Оср(N log2N). Требуется дополнительный массив, содержащий N элементов.

Структурное программирование приспособлено для описания действий, а ООП - для описания моделей. Абстракция – это суждение или представление о некотором объекте, которое содержит только свойства, являющиеся существенными в данном контексте. Абстракция – эффективное средство против сложности программирования, поскольку оно позволяет программисту сосредоточиться на существенных свойствах объекта и игнорировать менее важные свойства. Объектный стиль программирования связан с воздействием на объекты (говорят, с передачей объекту сообщений). При этом проектирование системы базируется на том условии, что никакая подсистема данного уровня не должна зависеть от устройства любой другой подсистемы этого уровня (взаимодействуют, но не зависят).Инкапсуляция – это процесс отделения друг от друга элементов объекта, определяющих его устройство и поведение; в частности, это скрытие переменных (полей) объекта с целью обеспечения доступа к ним только посредством методов класса. Идея инкапсуляции, в частности, реализована в модуле при его разделении на секции интерфейса и реализации.

Значительно упростить понимание сложных задач удается за счет усложнения иерархии. Усложнение иерархии от уровня к уровню достигается за счет наследования. Наследование – это расширение свойств наследника за счет принятия всех свойств предка.ООП использует также понятие "полиморфизма", состоящее в возможности переопределять методы класса-родителя. Иными словами, полиморфизм означает общий род действий, которые могут быть выполнены многими специфическими путями, в зависимости от того, какие объекты выполняют действия. Неразрывно с полиморфизмом связано понятие динамического связывания – возможность отложить подстановку реального адреса некоторой подпрограммы-метода с этапа компиляции (раннее связывание) до момента выполнения программы (позднее связывание), что используется для стандартизации работы с объектами. Любой объект в ООП обладает определенным поведением и состоянием. Поведение объекта – это то, как он реагирует на воздействия. Состояние объекта представляет собой суммарный результат его поведения. Сообщение, посланное объекту, активизирует совокупность операций над объектом, которая называется методом. Задавая структуру обмена сообщениями между объектами, программист получает совокупность операций, которые и составляют программу.

Основные типы операций над объектами

Внутренность объекта ОКРУЖНОСТЬ АПеременные Позиция 15,20 Размер 5Методы Форма- Маркер ПероВверх- Маркер СдвигК : Позиция- Маркер СдвигНа : Размер- Маркер ПероВниз- Маркер ЧертитьДугу : Размер,360 Высветить- Маркер Черный- Себе Форма Стереть- Маркер Белый- Себе Форма МАРКЕРМетоды ПероВверх ПероВниз Черный Белый СдвигК : X,Y СдвигНа : Z ЧертитьДугу : R, ... Сообщения (операции) объекту ОкружностьА:ОкружностьА.Высветить ОкружностьА.Стереть

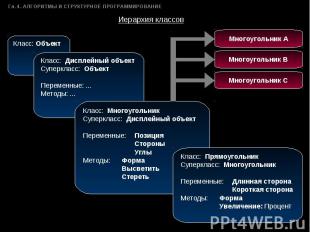
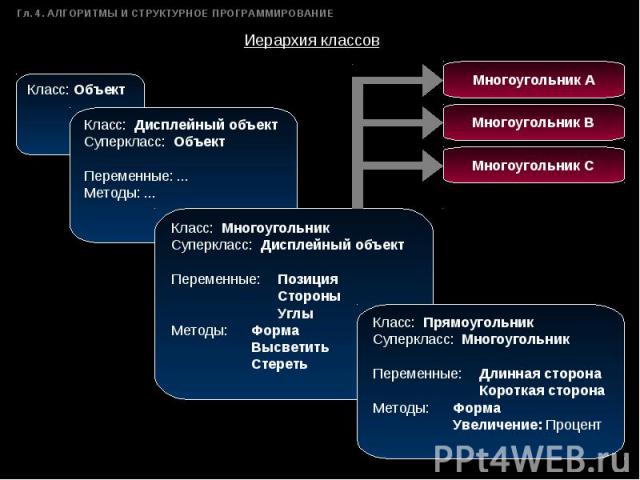
Иерархия классов Класс: Объект Класс: Дисплейный объектСуперкласс: ОбъектПеременные: ...Методы: ... Класс: МногоугольникСуперкласс: Дисплейный объектПеременные:ПозицияСтороныУглыМетоды:ФормаВысветитьСтереть Класс: ПрямоугольникСуперкласс: МногоугольникПеременные:Длинная сторонаКороткая сторонаМетоды:ФормаУвеличение: Процент Многоугольник C Многоугольник B Многоугольник А