Презентация на тему: Криптосистемы с открытым ключем

ЛекцияКриптосистемы с открытым ключем Лектор: профессор Яковлев В.А.

Хронология развития систем ЭЦП 1976 г. – открытие М. Хэлменом и У. Диффи асимметричных криптографических систем;1978 г. – Р. Райвест, А. Шамир, Л. Адельман – предложили первую систему ЭЦП, основанную на задаче факторизации большого числа;1985 г. – Эль Гамаль предложил систему ЭЦП, основанную на задаче логарифмирования в поле чисел из р элементов;1991 г.- Международный стандарт ЭЦП ISO/IEC 9796 (вариант РША);1994 г. – Стандарт США FIPS 186 (вариант подписи Эль Гамаля);1994 г. – ГОСТ Р 34.10-95 (вариант подписи Эль Гамаля);2000 г. – Стандарт США FIPS 186 – 2;2001 г. – ГОСТ Р 34.10-01 (ЭЦП на основе математического аппарата эллиптических кривых).

Односторонняя функция Пусть X и Y дискретные множества. Функция y=f(x), гдеx X , y Y называется односторонней (однонаправленной),если y легко вычисляется по любому x, а обратная функция x=f-1(y) является трудно вычислимой. Пример ОФ.y=ax(modp), где p- простое число, x - целое число,a -примитивный элемент поля Галуа GF(p). То есть a такое число, что все его степени ai(modp), i= 1,2…p-1,принимают все значения в множестве чисел от 1 до p-1.

Пример односторонней функции функции Пусть p=7, a=3. Проверим, что a примитивный элемент - a1 =3(mod7), a2 =2(mod7), a3 =6(mod7), a4 =4(mod7), a5 =5(mod7), a6 =1(mod7).Если x=4, то y=34(mod7)=4. Сложность нахождения функции возведения в степень Nв=O(2logp).Обратная функция x=logay (функция дискретного логарифмирования) трудно вычислима. Если p - сильно простое число, то Nлог=O((p)1/2).

Оценки сложности вычислений прямой и обратной функций Пусть 1000 разрядное двоичное число, тогда для решения задачи возведения в степень числа х по modp потребуется примерно 2000 = 2*103 операций , а для нахождения логарифма такого числа потребуется примерноp1/2=2500~10170 операций, что вычислительно невозможно осуществить ни за какое реально обозримое время.

Односторонняя функция с потайным ходом Это не просто ОФ, обращение которой невозможно, она содержит потайной ход (trapdoor), который позволяет вычислять обратную функцию, если известен секретный параметр - ключ. y=f(x,s) – легковычислима; x=f-1(y) – трудновычислима; x= f-1(y,s)- легковычислима.

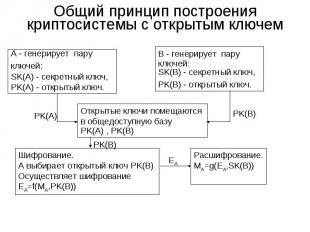
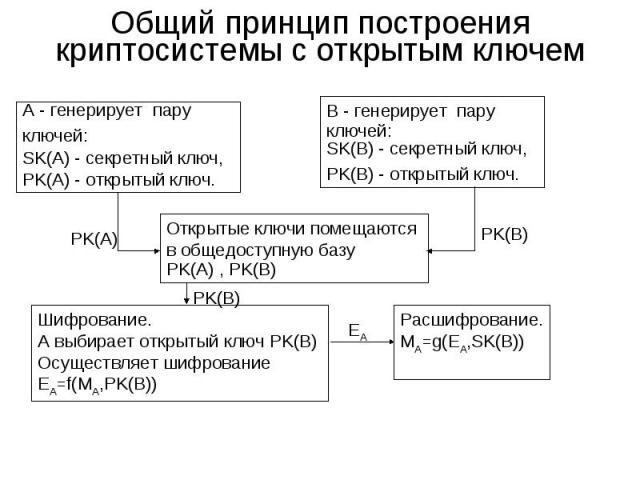
Общий принцип построения криптосиcтемы с открытым ключем А - генерирует паруключей:SK(A) - секретный ключ,PK(A) - открытый ключ. B - генерирует паруключей:SK(B) - секретный ключ,PK(B) - открытый ключ. Открытые ключи помещаются в общедоступную базуPK(A) , PK(B) Шифрование.А выбирает открытый ключ PK(B) Осуществляет шифрованиеEA=f(MA,PK(B)) Расшифрование.MA=g(EA,SK(B))

Требования к системам с открытым ключем 1. Вычисление пары ключей PK, SK должно быть просто решаемой задачей;2. При известном ключе шифрования PK вычисление криптограммы E=f(M,PK) должно быть простым;3. При известном ключе расшифрования SK восстанавливает сообщение M=g(E,SK) должно быть простым;4. При известном ключе шифрования PK вычисление ключа расшифрования SK должно быть сложным;5. При известном ключе шифрования PK, но неизвестном ключе расшифрования SK вычисление М по известной криптограмме E должно быть весьма сложным.

Система шифрования Эль-Гамаля Пусть p -простое число; a - примитивный элемент. Генерирование пары открытых ключейA - генерирует число xA, вычисляет открытый ключyA=ax (modp). (SK= xA , PK= yA). yA передается корр. B. Шифрование сообщенияПусть корр. B хочет послать корр.А сообщение m<p. Генерирует случайное число k<p.Формирует криптограмму E=(c1c2)c1=ak(modp), c2=m(yA-1)k .Отправляет E корр. А.

Система шифрования Эль-Гамаля Расшифрование сообщения.Корр.А вычисляет c1x (modp) = akx (modp) ,Затем находитc2akx (modp)= m(yA-1)k akx (modp)= ma-xk akx (modp)=m Замечание.Как найти yA-1 ? yAp-2 (modp)= yAp-1 (modp) yA-1 (modp) = yA-1 (modp)

Стойкость системы Эль-Гамаля 1. Раскрытие секретного ключа эквивалентно решению задачи дискретного логарифмирования.2. Нахождение m без знания ключа возможно, если случайное число k используется дважды и в одном случае нарушитель знает открытый текстc2= m(yA-1)k (modp), c’2= m’(yA-1)k (modp) Зная c2, c’2 и m несложно найти m’ m’= c’2mc-12 (modp)k должно меняться случайным образом при шифровании нового сообщения.

Пример системы Эль-Гамаля p=11, a=4, a- примитивный элемент GF(2p) Пусть x=3 – закрытый ключy=43(mod11)=64(mod11)=9 открытый ключ Генерирование СЧ k=4Вычисление:С1=ak(modp)=44(mod11)=256(mod11)=3y-1=yp-2(modp)= 99(mod11)=929292929(mod11)=4*4*4*4*9(mod11)=5*5*9(mod11)=5C2=my-1k(modp)=6*54(mod11)=6*3*3(mod11)=10 C1x (modp)=33(mod11)=5C2*C1x (modp)=10*5 (mod11)=50(mod11)=6

Система РША (1978г.) Генерирование ключей.Случайно выбираются два простых числа p и q. Находится модуль N=pq. Находится функция Эйлера (N)= (p-1)(q-1).Выбираем число e такое, что НОД(e, (N))=1. Находим d, как обратный элемент к e, de=1(mod (N)).Объявляем d=SK, (e,N)=PK. PK сообщается всем корреспондентам. Шифрование.Корр. А передает зашифрованное сообщение корр.В(использует открытый ключ корр. В)E=me(modN) Расшифрование.Корр. В расшифровывает принятую криптограмму от корр.А,используя свой секретный ключ.m=Ed(modN)

Доказательство обратимости операции дешифрования операции шифрования Покажем, что Ed(modN) =(me)d(modN) =mПо т. Эйлера m(N)1(modN) для любого m взаимно простого с N. Умножая обе части сравнения на m, получаем сравнение m(N)+1 m(modN) справедливое уже для любого целого m. Перепишем соотношение ed1(mod(N)) в виде ed=1+k(N) для некоторого целого k.Тогда Ed=(me)d=m1+k(N)= m1+(N) m(k-1)(N)= =m m(k-1)(N)= m1+(k-1)(N) =m1+(N) m(k-2)(N)= …. = m1+(N) =mЧто и требовалось доказать.

Пример системы РША p=3, q=11 N=33 Генерирование ключейe=7, НОД(7,20)=1d=7-1(mod20) = 3 Шифрование m=6 E=me(modN)= 67(mod33)=62 62 62 61(mod33)==3*3*3*3*2=30 РасшифрованиеEd(modN)=303(mod33)=900*30(mod33)=9*30(mod33)=6

Оценки стойкости системы РША 1. Нахождение чисел p и q по известному модулю N. Задача факторизации имеет сложность O((N)1/2).2. Будем последовательно возводить полученную криптограмму в степень равную значению открытого ключа т.е. (((((Ee)e)…..)e . Если при некотором шаге окажется, что Ei=E , то это означает, что Ei-1=m. Доказывается, что данная атака требует непереборно большого числа шагов. 3. Поиск слабых ключей, для которых me’ = m , т.е. возведение в степень не меняет сообщения. Эта атака имеет малую вероятность успеха, если p и q выбираются среди сильно простых чисел. Сильно простое число, это число, для которого p-1 не содержит в разложении маленьких сомножителей, и имеет в разложении хотя бы один большой сомножитель. 4.

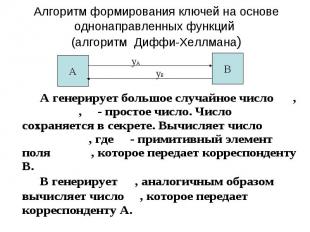
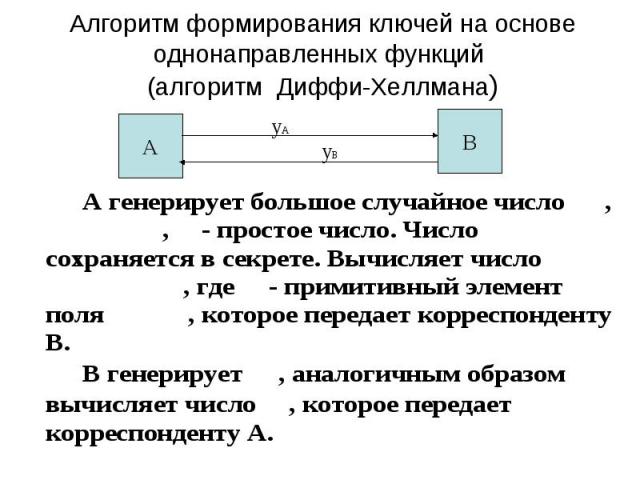
Алгоритм формирования ключей на основе однонаправленных функций (алгоритм Диффи-Хеллмана)

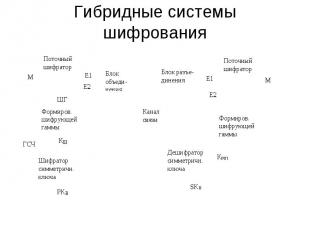
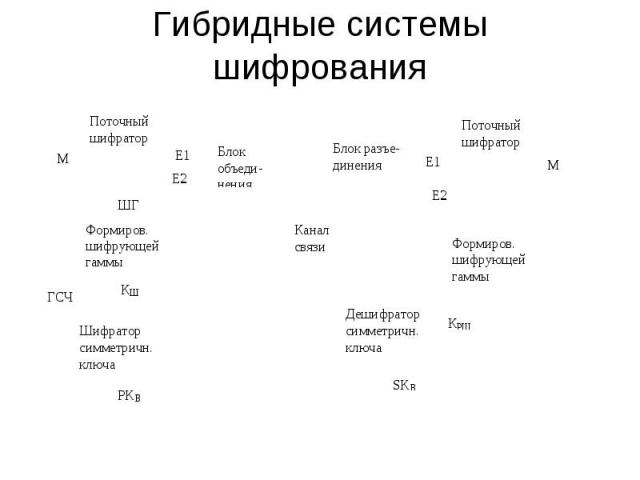
Гибридные системы шифрования