Презентация на тему: Криптография: алгоритм RSA

Криптография:алгоритм RSA Выполнила: Ученица 8а класса.Семёнова Екатерина ВадимовнаНаучный руководитель:Князькина Татьяна Викторовна

Цели и задачи Цель проекта : изучение системы шифрования с открытым ключом RSA. Задачи проекта:Ознакомиться с основными понятиями криптографии.Изучение основных принципов симметрических криптосистем.Изучение основных принципов асимметрических криптосистем.Ознакомиться с методами теории чисел, используемых в RSA.Изучение алгоритма RSA.Продемонстрировать на примерах шифрование и дешифрование различных сообщений по алгоритму RSA

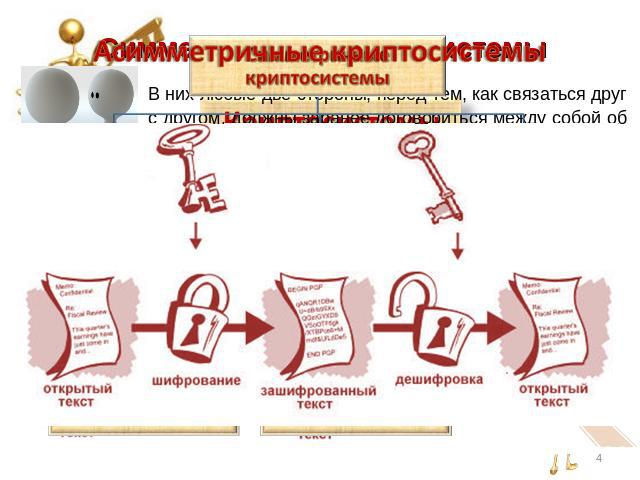
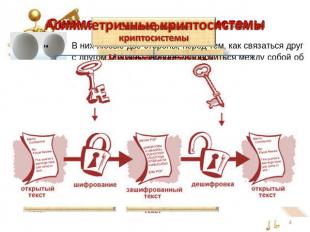
Основные понятияКриптология (kryptos - тайный, logos - наука) - наука, изучающая математические методы защиты информации путем ее преобразования.Криптография - занимается поиском и исследованием математических методов преобразования информации.Криптоанализ - занимается исследованием возможности расшифровывания информации без знания ключей.Шифрование - преобразовательный процесс: исходный текст, который носит также название открытого текста, заменяется шифрованным текстом (называемый также криптограммой) . Дешифрование - обратный шифрованию процесс. На основе ключа шифрованный текст преобразуется в исходный.

Асимметричные криптосистемы Симметричные криптосистемыЗаменыКвадрат ПолибияПляшущие человечки А. Конан Дойля….ПерестановкиСциталлаШифр ЦезаряКвадрат Вижинира….Комбинированные

Шифрование и дешифрование: cхема RSAСообщением являются целые числа лежащие от 0 до m-1. Алгоритм создания открытого и секретного ключей RSAВыберем два простых числа p и q. Вычисляется их произведение m= pq, которое называется модулем. Вычисляется значение функции Эйлера от числа m: (m)=(p-1)(q-1)Выбирается целое число e (1<e<(m)), взаимно простое со значением функции (m). Ищется линейное представление НОД (e, (m)) =1=de+c(m) и вычисляется число d. (Обычно, оно вычисляется при помощи расширенного алгоритма Евклида. ). Пара (e,m) публикуется в качестве открытого ключа RSA.Пара (d,m) играет роль секретного ключа RSA и держится в секрете. Делители p и q можно либо уничтожить либо сохранить вместе с секретным ключом. Алгоритм шифрованияВзять открытый ключ (e,m) .Взять открытый текст 0 a m-1Получить криптограмму b:b=ae mod mПередать шифрованное сообщение b.

Алгоритм RSA: пример. Алгоритм шифрованияВозьмем открытый ключ (e,m)=(5,85) .Возьмем открытый текст a=7.Получить криптограмму b:b=ae mod m=75 mod 85=16807 mod 85=62Передать шифрованное сообщение b=62. Алгоритм дешифрованияПринять зашифрованное сообщение b=62.Применить свой секретный ключ (d,m)=(13,85) для расшифровки сообщения: a=bd mod m=6213 mod 85=200028539268669788905472 mod 85=7 Пара (d,m)=(13,85) – секретный ключ RSA.

Криптоанализ RSA Почему же систему RSA трудно взломать? Ловушка в системе RSA заключается в том, что умножение чисел p и q для получения числа m — простая операция, тогда как обратная задача — разложение числа m на множители для получения p и q — практически неразрешима.

Основные результаты работы Изучены основные виды симметрических криптосистем: шифры замены и шифры перестановки.Изучены основные принципы асимметрических криптосистем.Изучены понятия и методы теории чисел, используемых в RSA: алгоритм Евклида нахождения НОД, расширенный алгоритм Евклида, функция Эйлера и ее свойства.Изучен алгоритма RSA.Разобрано 5 примеров шифрования и дешифрования различных высказываний великих математиков по алгоритму RSA