Презентация на тему: Алгоритмы на графах. Топологическая сортировка отсечением вершин

Алгоритмы на графах Топологическая сортировка отсечением вершин Югов Иван Олегович МОУ Гимназия №10, г. Тверь

Нахождение компонент связности В первой строке файла input.txt заданы целые n и m — соответственно число вершин и число рёбер неориентированного графа (1 ≤ n ≤ 10 000, 0 ≤ m ≤ 50 000). В следующих m строках файла заданы пары номеров вершин, соединённых рёбрами. В файл output.txt вывести единственное число — количество компонент связности графа. Ограничение по времени — 1 сек. Ограничение по памяти — 16 Мб.

Домашнее задание Сколько различных путей есть в дереве с n вершинами? Какое максимальное количество циклов (длиной 3 и более) может быть в неориентированном графе с n вершинами? Какое максимальное количество циклов (длиной 3 и более) может быть в неориентированном графе с n вершинами и k компонентами связности? Написать программу, определяющую количество компонент связности, с использованием матрицы смежности. Написать программу, определяющую максимальный размер компоненты связности, с использованием списка смежности.

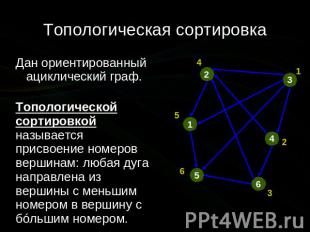
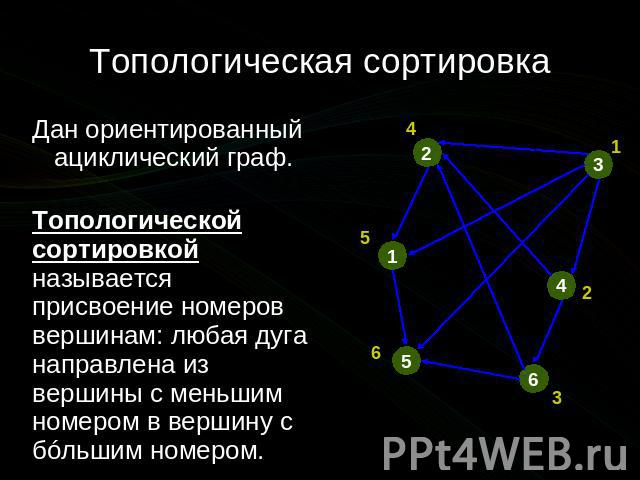
Топологическая сортировка Дан ориентированный ациклический граф. Топологической сортировкой называется присвоение номеров вершинам: любая дуга направлена из вершины с меньшим номером в вершину с бóльшим номером.

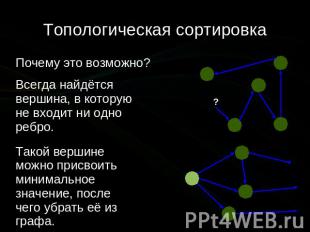
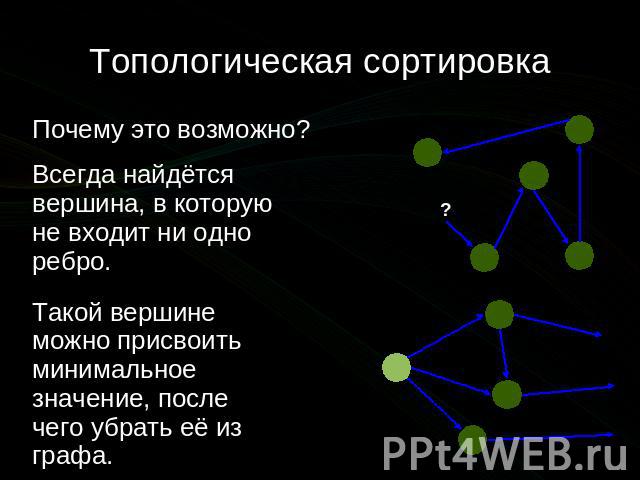
Топологическая сортировка Почему это возможно? Всегда найдётся вершина, в которую не входит ни одно ребро. Такой вершине можно присвоить минимальное значение, после чего убрать её из графа.

Топологическая сортировка Как быстро определить вершины, в которые не входит ни одно ребро? Будем хранить входящую степень каждой вершины: массив deg_in длины n, deg_in[i]— число соседей i-й вершины. Pascal ... a[u, v] := True; Inc(deg_in[v]); ... C ... a[u, v] = TRUE; deg_in[v]++; ...

Топологическая сортировка массив order длины n, order[i] — присвоенный i-й вершине порядковый номер при топологической сортировке; currorder — текущий присваиваемый номер. Pascal for i := 1 to n do order[i] := 0; currorder := 0; TopSort; TopSort: for i := 1 to n do for j := 1 to n do if (deg_in[j] = 0) and (order[j] = 0) then begin Inc(currorder); order[j] := currorder; for <u - сосед j-й вершины> do Dec(deg_in[u]); end; C for(i = 0; i < n; i++) order[i] = 0; currorder = 0; TopSort; TopSort: for(i = 0; i < n; i++) for(j = 0; j < n; j++) if((!deg_in[j]) && (!order[j])) { order[j] = ++currorder; for(<u - сосед i-й вершины>) deg_in[u]--; };

Топологическая сортировка В первой строке файла input.txt заданы целые n и m — соответственно число вершин и число рёбер ориентированного графа (1&nbsp;≤&nbsp;n&nbsp;≤&nbsp;10&nbsp;000, 0&nbsp;≤&nbsp;m&nbsp;≤&nbsp;50&nbsp;000). В следующих m строках файла заданы пары номеров вершин, соединённых рёбрами. В файл output.txt вывести номера, которые приобретут вершины после топологической сортировки. i-е число означает номер, приобретённый i-й вершиной. Ограничение по времени — 3 сек. Ограничение по памяти — 16 Мб.

Топологическая сортировка В первой строке файла input.txt заданы целые n и m — соответственно число вершин и число рёбер ориентированного графа (1&nbsp;≤&nbsp;n&nbsp;≤&nbsp;10&nbsp;000, 0&nbsp;≤&nbsp;m&nbsp;≤&nbsp;50&nbsp;000). В следующих m строках файла заданы пары номеров вершин, соединённых рёбрами. В файл output.txt вывести упорядоченные топологически номера вершин. Ограничение по времени — 3 сек. Ограничение по памяти — 16 Мб.

Домашнее задание Предприятие «Авто-2010» выпускает двигатели известных во всём мире автомобилей. Двигатель состоит ровно из n деталей, пронумерованных от 1 до n, при этом деталь с номером i изготавливается за pi секунд. Специфика предприятия «Авто-2010» заключается в том, что там одновременно может изготавливаться лишь одна деталь двигателя. Для производства некоторых деталей необходимо иметь предварительно изготовленный набор других деталей. Генеральный директор «Авто-2010» поставил перед предприятием амбициозную задачу — за наименьшее время изготовить деталь с номером 1, чтобы представить её на выставке. Требуется написать программу, которая по заданным зависимостям порядка производства между деталями найдёт наименьшее время, за которое можно произвести деталь с номером 1.

Домашнее задание Первая строка входного файла details.in содержит число n (1&nbsp;≤&nbsp;n&nbsp;≤&nbsp;10&nbsp;000) — количество деталей двигателя. Вторая строка содержит n натуральных чисел p1, p2, …, pn, определяющих время изготовления каждой детали в секундах. Время для изготовления каждой детали не превосходит 109 секунд. Каждая из последующих n строк входного файла описывает характеристики производства деталей. Здесь i-я строка содержит число деталей ki, которые требуются для производства детали с номером i, а также их номера. Сумма всех чисел ki не превосходит 200000. Известно, что не существует циклических зависимостей в производстве деталей. В первой строке выходного файла details.out должны содержаться два числа: минимальное время ( в секундах), необходимое для скорейшего производства детали с номером 1 и число k деталей, которые необходимы для этого производства. Во второй строке требуется вывести через пробел k чисел — номера деталей в том порядке, в котором их следует производить для скорейшего производтсва детали с номером 1. Ограничение по времени — 2 сек. Ограничение по памяти — 64 Мб.

Домашнее задание

Источники Курс «Базовые алгоритмы для школьников» (Станкевич А. С., Абакумов К. В., Мухачёва М. А.) «Интернет-уинверситет информационных технологий» http://www.intuit.ru/department/algorithms/basicalgos/