Презентация на тему: Перпендикуляр

Перпендикуляр Перпендикуляром, опущенным из точки A на прямую а, называется отрезок AB, соединяющий точку A с точкой B прямой a, перпендикулярный прямой a.Точка B называется основанием перпендикуляра. расстоянием от точки A до прямой a.

НаклонныеДля произвольной точки C прямой a, отличной от основания перпендикуляра B, отрезок AC называетсянаклонной, проведенной из точки A к прямой a.Точка C называетсяОтрезок BC называется

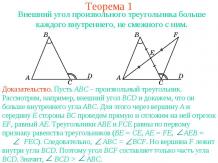
ТеоремаПерпендикуляр, опущенный из данной точки на данную прямую, короче всякой наклонной, проведенной из этой точки к этой прямой. Иначе говоря, расстояние от точки до прямой является наименьшим из расстояний от этой точки до точек данной прямой.

Вопрос 1Что называется перпендикуляром, опущенным из данной точки на данную прямую? Ответ: Перпендикуляром, опущенным из данной точки A на данную прямую а, называется отрезок AB, соединяющий точку A с точкой B прямой a, перпендикулярный прямой a.

Вопрос 2Что называется наклонной, проведенной из данной точки к данной прямой? Ответ: Наклонной, проведенной из точки A к прямой a, называется отрезок AC, соединяющей точку A с произвольной точкой C прямой a, отличной от основания перпендикуляра B.

Вопрос 3Что называется расстоянием от точки до прямой?Ответ: Длина перпендикуляра, опущенного из данной точки на данную прямую.

Вопрос 4Что больше, перпендикуляр или наклонная, проведенные из одной точки к данной прямой?

Упражнение 1Сколько перпендикуляров можно опустить из данной точки на данную прямую.

Упражнение 2Сколько наклонных можно провести из данной точки к данной прямой.

Упражнение 3Длина какого отрезка является расстоянием от вершины треугольника до его противоположной стороны?

Упражнение 4Могут ли неравные наклонные, проведенные из одной точки к одной прямой, иметь равные проекции?

Упражнение 5Могут ли равные наклонные, проведенные из одной точки к одной прямой, иметь неравные проекции?

Упражнение 6Чему равна проекция одной стороны равностороннего треугольника на прямую, содержащую другую его сторону? Ответ: Половине стороны треугольника.

Упражнение 7Чему равна проекция гипотенузы прямоугольного треугольника на его на прямую, содержащую его катет?

Упражнение 8Чему равна проекция боковой стороны равнобедренного треугольника на его основание

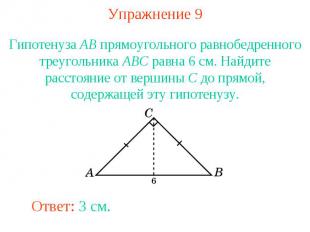
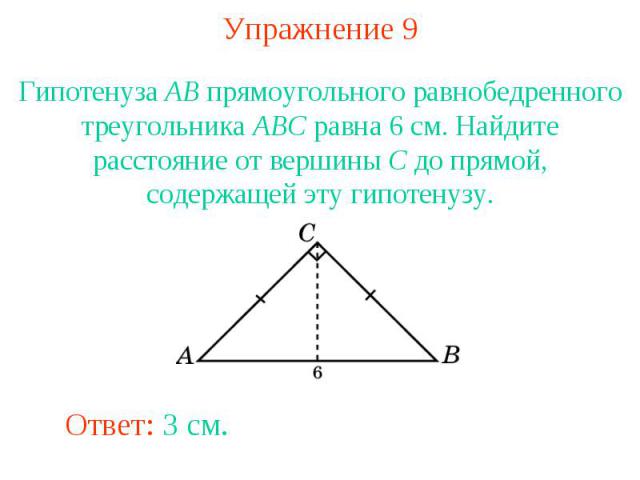
Упражнение 9Гипотенуза AB прямоугольного равнобедренного треугольника ABC равна 6 см. Найдите расстояние от вершины C до прямой, содержащей эту гипотенузу.

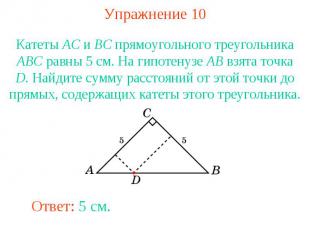
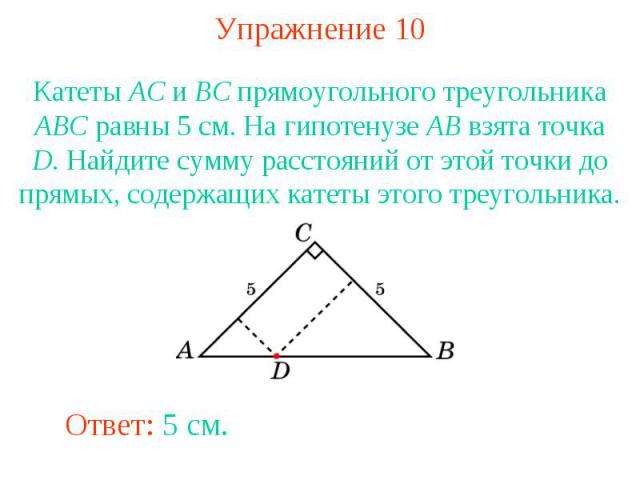
Упражнение 10Катеты AC и BC прямоугольного треугольника ABC равны 5 см. На гипотенузе AB взята точка D. Найдите сумму расстояний от этой точки до прямых, содержащих катеты этого треугольника.

Упражнение 11Катеты AC и BC прямоугольного треугольника ABC равны 3 см и 4 см. На гипотенузе AB взята точка D. В каких пределах находится сумма S расстояний от этой точки до прямых, содержащих катеты этого треугольника.

Задача ГеронаЗадача. Дана прямая с и две точки А и В на плоскости. Найдите такую точку С на этой прямой, чтобы сумма расстояний АС + СВ была наименьшей. Решение. В случае, если точки A и B лежат по разные стороны от прямой c, то искомой точкой C является точка пересечения отрезка AB и прямой c. Действительно, для любой другой точки C’ прямой c имеем: AC’+C’B >AC + CB.Если точки A и B лежат по одну сторону от прямой c, то для нахождения искомой точки C заменим точку B на точку B', симметричную B относительно прямой c. Тогда BC=B’C и этот случай сводится к предыдущему.

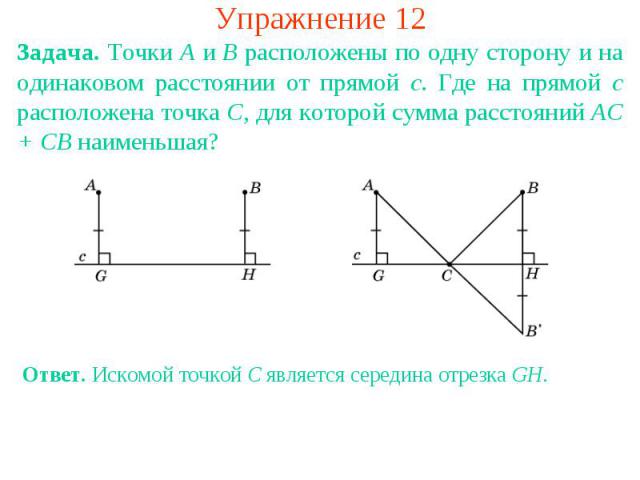
Упражнение 12Задача. Точки A и B расположены по одну сторону и на одинаковом расстоянии от прямой c. Где на прямой c расположена точка C, для которой сумма расстояний AC + CB наименьшая? Ответ. Искомой точкой C является середина отрезка GH.

Упражнение 13Дана прямая с и две точки А и В по одну сторону от нее. Точка С на прямой c обладает тем свойством, что сумма расстояний АС + СВ – наименьшая. Докажите, что угол 1 равен углу 2.Доказательство. Рассмотрим точку B’, симметричную точке B относительно прямой c. Углы 1 и 3 равны, как вертикальные. Углы 2 и 3 равны, как соответственные углы в равных треугольниках BCH и B’CH. Следовательно, угол 1 равен углу 3.

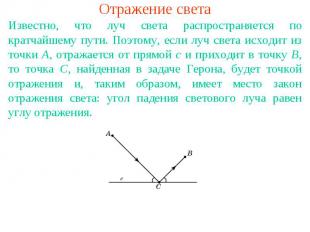
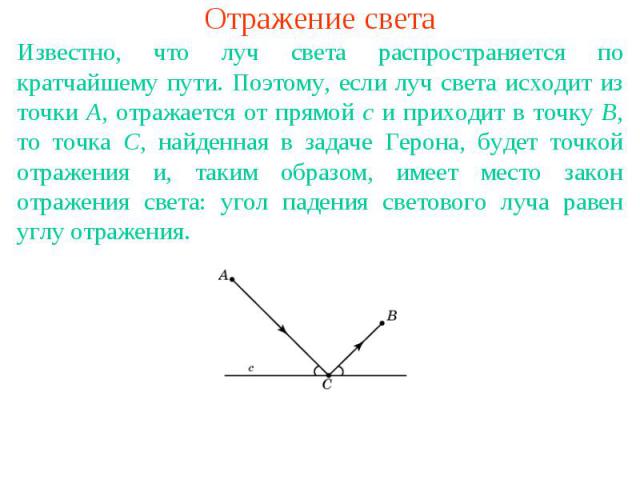
Отражение светаИзвестно, что луч света распространяется по кратчайшему пути. Поэтому, если луч света исходит из точки A, отражается от прямой c и приходит в точку B, то точка C, найденная в задаче Герона, будет точкой отражения и, таким образом, имеет место закон отражения света: угол падения светового луча равен углу отражения.