Презентация на тему: Перпендикуляр и наклонная

Перпендикуляр и наклонная Урок геометрии в 10 классе

На одном из предыдущих уроков вы познакомились с понятием проекции точки на данную плоскость параллельно данной прямой. На этом уроке вы продолжите изучение прямых и плоскостей; узнаете, как находится угол между прямой и плоскостью. Вы познакомитесь с понятием ортогональной проекции на плоскость и рассмотрите ее свойства. На уроке будут даны определения расстояния от точки до плоскости и от точки до прямой, угла между прямой и плоскостью. Будет доказана знаменитая теорема о трех перпендикулярах.

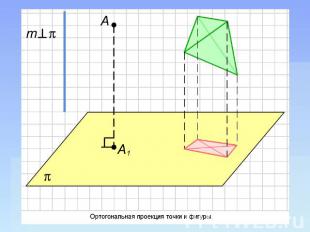
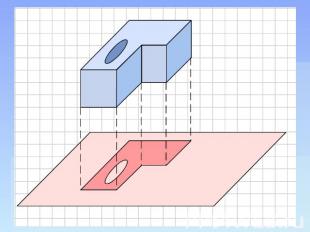
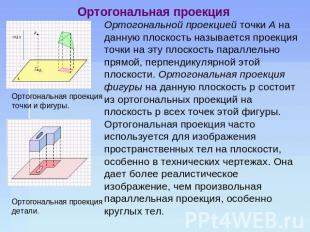
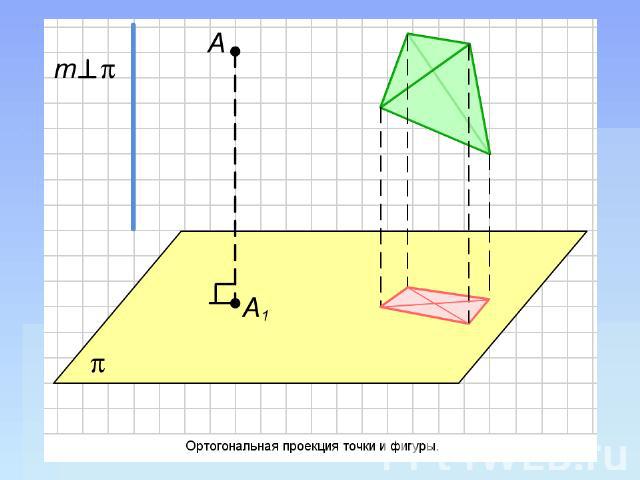
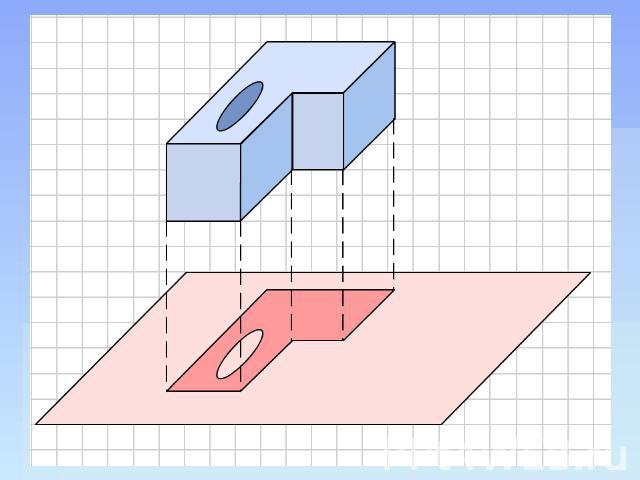
Ортогональная проекция Ортогональной проекцией точки А на данную плоскость называется проекция точки на эту плоскость параллельно прямой, перпендикулярной этой плоскости. Ортогональная проекция фигуры на данную плоскость p состоит из ортогональных проекций на плоскость p всех точек этой фигуры. Ортогональная проекция часто используется для изображения пространственных тел на плоскости, особенно в технических чертежах. Она дает более реалистическое изображение, чем произвольная параллельная проекция, особенно круглых тел.

Перпендикуляр и наклонная Пусть через точку А, не принадлежащую плоскости p, проведена прямая, перпендикулярная этой плоскости и пересекающая ее в точке В. Тогда отрезок АВ называется перпендикуляром, опущенным из точки А на эту плоскость, а сама точка В — основанием этого перпендикуляра. Любой отрезок АС, где С — произвольная точка плоскости p, отличная от В, называется наклонной к этой плоскости. Заметим, что точка В в этом определении является ортогональной проекцией точки А, а отрезок АС — ортогональной проекцией наклонной AВ. Ортогональные проекции обладают всеми свойствами обычных параллельных проекций, но имеют и ряд новых свойств.

Свойства ортогональной проекции Пусть из одной точки к плоскости проведены перпендикуляр и несколько наклонных. Тогда справедливы следующие утверждения. 1. Любая наклонная длиннее как перпендикуляра, так и ортогональной проекции наклонной на эту плоскость. 2. Равные наклонные имеют и равные ортогональные проекции, и наоборот, наклонные, имеющие равные проекции, также равны. 3. Одна наклонная длиннее другой тогда и только тогда, когда ортогональная проекция первой наклонной длиннее ортогональной проекции второй наклонной.

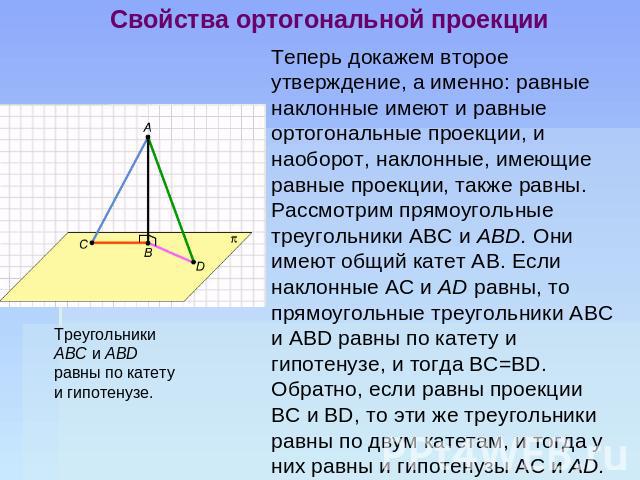
Свойства ортогональной проекции Доказательство. Пусть из точки А к плоскости p проведены перпендикуляр АВ и две наклонные АС и AD; тогда отрезки ВС и BD — ортогональные проекции этих отрезков на плоскость p. Докажем первое утверждение: любая наклонная длиннее как перпендикуляра, так и ортогональной проекции наклонной на эту плоскость. Рассмотрим, например, наклонную AС и треугольник ABC, образованный перпендикуляром AВ, этой наклонной AС, и ее ортогональной проекцией ВС. Этот треугольник прямоугольный с прямым углом в вершине В и гипотенузой AС, которая, как мы знаем из планиметрии, длиннее каждого из катетов, т.е. и перпендикуляра AВ, и проекции ВС. Из точки А к плоскости pi проведены перпендикуляр АВ и две наклонные AC и AD.

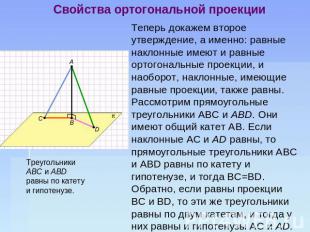
Свойства ортогональной проекции Теперь докажем второе утверждение, а именно: равные наклонные имеют и равные ортогональные проекции, и наоборот, наклонные, имеющие равные проекции, также равны. Рассмотрим прямоугольные треугольники AВС и ABD. Они имеют общий катет AВ. Если наклонные AС и AD равны, то прямоугольные треугольники AВС и AВD равны по катету и гипотенузе, и тогда BC=BD. Обратно, если равны проекции ВС и BD, то эти же треугольники равны по двум катетам, и тогда у них равны и гипотенузы AС и AD.

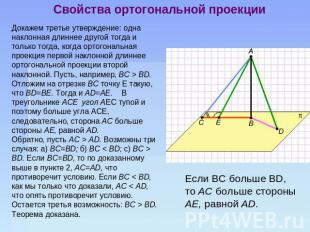
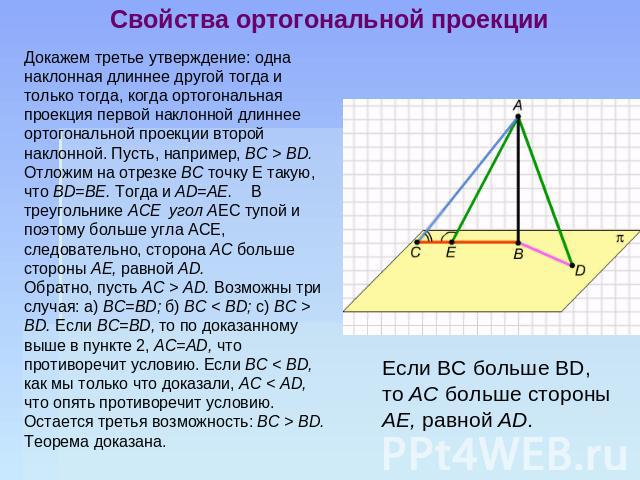
Свойства ортогональной проекции Докажем третье утверждение: одна наклонная длиннее другой тогда и только тогда, когда ортогональная проекция первой наклонной длиннее ортогональной проекции второй наклонной. Пусть, например, ВС > BD. Отложим на отрезке ВС точку Е такую, что BD=BE. Тогда и AD=AE. В треугольнике АСЕ угол AEC тупой и поэтому больше угла ACE, следовательно, сторона АС больше стороны АЕ, равной AD. Обратно, пусть АС > AD. Возможны три случая: a) BC=BD; б) ВС < BD; с) ВС > BD. Если BC=BD, то по доказанному выше в пункте 2, AC=AD, что противоречит условию. Если ВС < BD, как мы только что доказали, АС < AD, что опять противоречит условию. Остается третья возможность: ВС > BD. Теорема доказана.

Расстояние от точки до плоскости Расстоянием от точки до плоскости (не проходящей через эту точку) называется длина перпендикуляра, опущенного из точки на эту плоскость. Из теоремы о свойствах ортогональной проекции следует, что расстояние от точки А до плоскости pi равно наименьшему расстоянию от точки А до точек этой плоскости.

Свойство расстояний от разных точек до плоскости Замечание 1 (свойство расстоянии от разных точек до плоскости). Пусть две точки А и В не принадлежат плоскости pi, а прямая АВ пересекает плоскость pi в точке С. Тогда расстояния от точек А и В до плоскости pi относятся как отрезки АС и ВС:

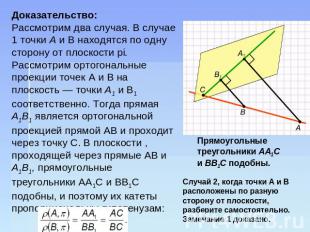
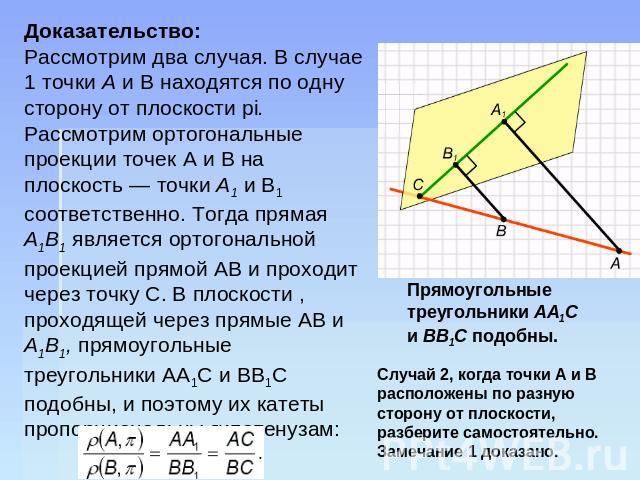
Доказательство: Рассмотрим два случая. В случае 1 точки А и В находятся по одну сторону от плоскости pi. Рассмотрим ортогональные проекции точек А и В на плоскость — точки А1 и B1 соответственно. Тогда прямая A1B1 является ортогональной проекцией прямой AВ и проходит через точку С. В плоскости , проходящей через прямые AВ и А1В1, прямоугольные треугольники AA1С и BB1C подобны, и поэтому их катеты пропорциональны гипотенузам: Прямоугольные треугольники AA1C и ВВ1С подобны. Случай 2, когда точки А и В расположены по разную сторону от плоскости, разберите самостоятельно. Замечание 1 доказано.

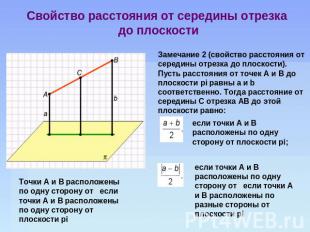
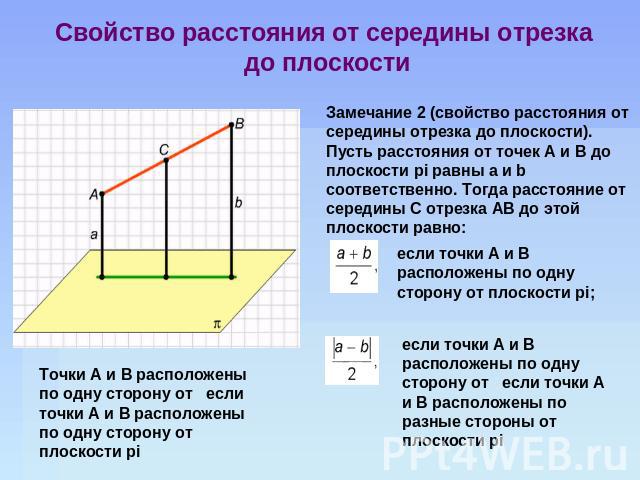
Свойство расстояния от середины отрезка до плоскости Замечание 2 (свойство расстояния от середины отрезка до плоскости). Пусть расстояния от точек А и B до плоскости pi равны а и b соответственно. Тогда расстояние от середины С отрезка АВ до этой плоскости равно: если точки A и B расположены по одну сторону от плоскости pi; если точки A и B расположены по одну сторону от если точки А и B расположены по разные стороны от плоскости pi Tочки A и B расположены по одну сторону от если точки А и B расположены по одну сторону от плоскости pi

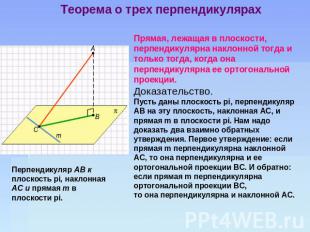
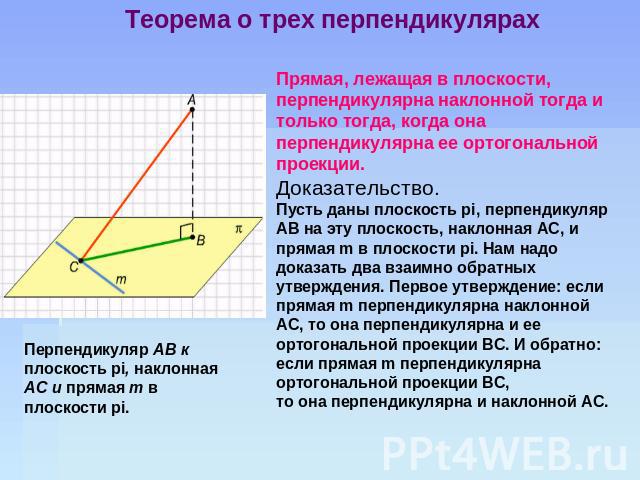
Теорема о трех перпендикулярах Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна ее ортогональной проекции. Доказательство. Пусть даны плоскость pi, перпендикуляр АВ на эту плоскость, наклонная АС, и прямая m в плоскости pi. Нам надо доказать два взаимно обратных утверждения. Первое утверждение: если прямая m перпендикулярна наклонной АС, то она перпендикулярна и ее ортогональной проекции ВС. И обратно: если прямая m перпендикулярна ортогональной проекции ВС, то она перпендикулярна и наклонной АС. Перпендикуляр АВ к плоскость pi, наклонная АС и прямая т в плоскости pi.

Прямая m перпендикулярна плоскости АВС.

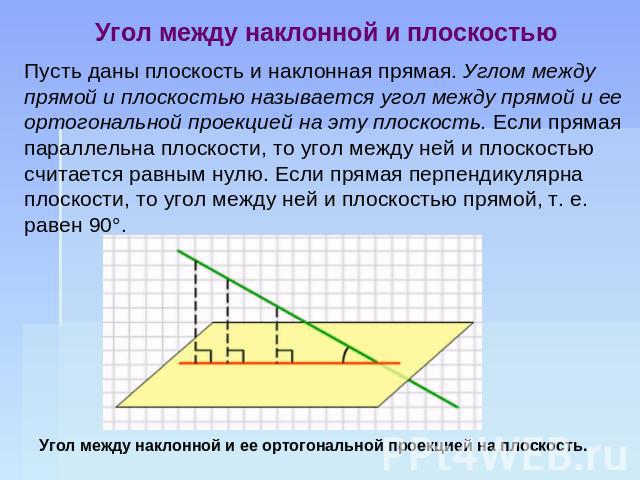
Угол между наклонной и плоскостью Пусть даны плоскость и наклонная прямая. Углом между прямой и плоскостью называется угол между прямой и ее ортогональной проекцией на эту плоскость. Если прямая параллельна плоскости, то угол между ней и плоскостью считается равным нулю. Если прямая перпендикулярна плоскости, то угол между ней и плоскостью прямой, т. е. равен 90°.

Перпендикуляр, наклонная и ее ортогональная проекция образуют прямоугольный треугольник.

Автор: Аверкина Т.П., учитель МОУ «Тархановская СОШ» Ичалковского района РМ