Презентация на тему: Ломаная

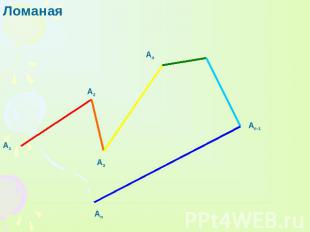
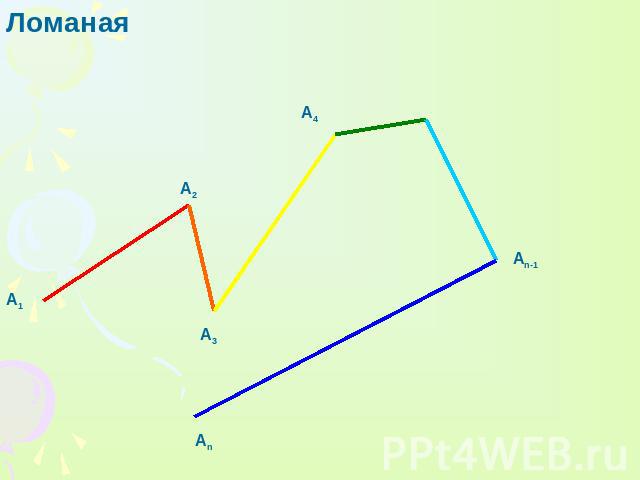
Ломаная

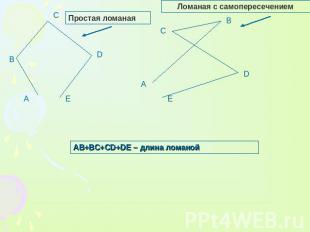
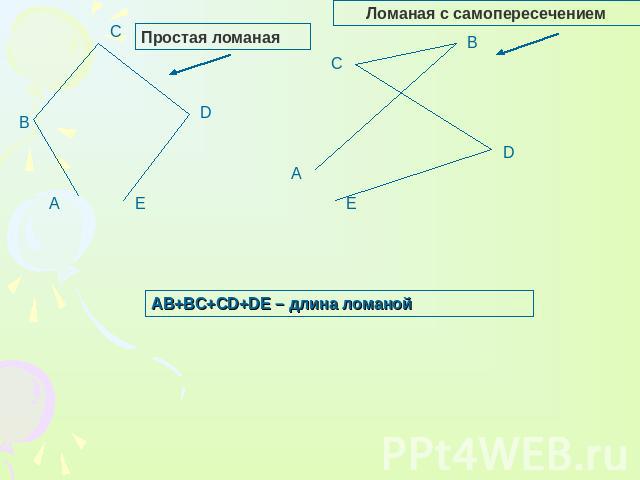
Ломаная с самопересечением Простая ломаная AB+BC+CD+DE – длина ломаной

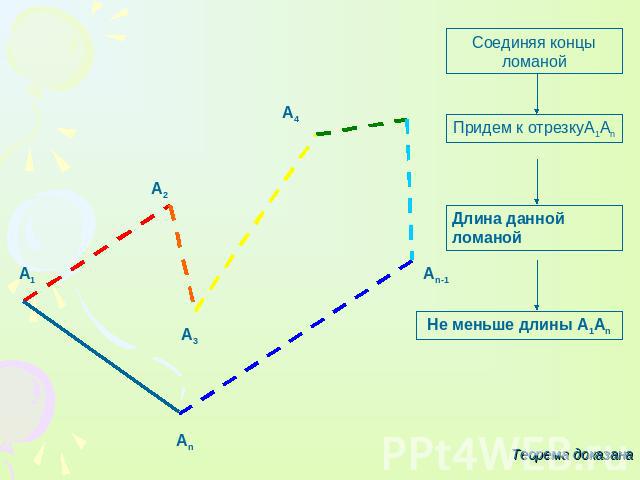
ТЕОРЕМА 13.1 Длина ломаной не меньше длины отрезка, соединяющего ее концы

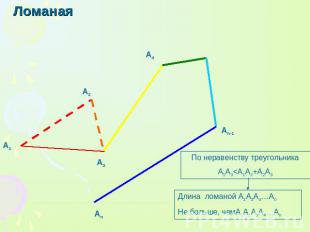
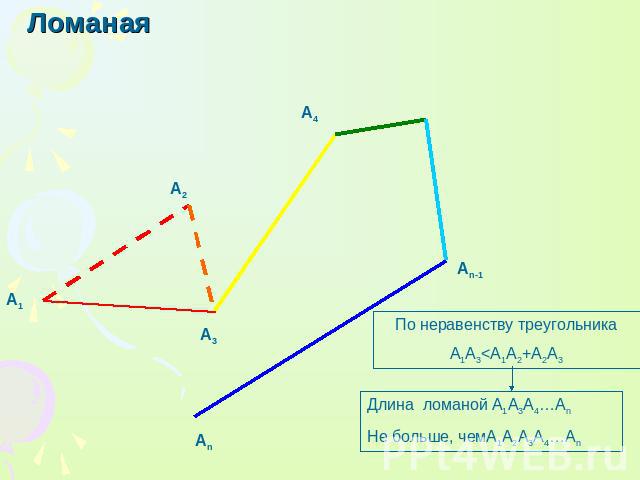
Ломаная По неравенству треугольника A1A3<A1A2+A2A3 Длина ломаной А1А3А4…Аn Не больше, чемА1А2А3А4…Аn

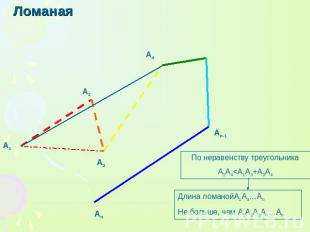
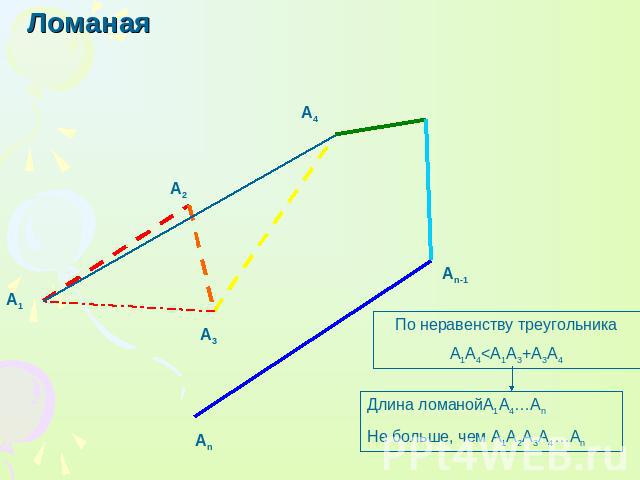
Ломаная По неравенству треугольника A1A4<A1A3+A3A4 Длина ломанойА1А4…Аn Не больше, чем А1А2А3А4…Аn

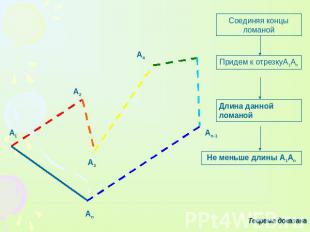
Соединяя концы ломаной Придем к отрезкуА1Аn Длина данной ломаной Не меньше длины А1Аn

Вопросы 1. Какая фигура называется ломаной? 2. Что называют вершиной ломаной? 3. Что называют звеном ломаной 4. Когда ломаная будет прямой? 5. Когда ломаная будет с самопересечением? 6. Сформулируйте теорему 13.1.

Решение задач №6 – устно 2. Найдите длину ломаной А1А2А3А4А5А6, если А1, А2, А3, А4 – вершины квадрата со стороной 2см, А5 – точка пересечения диагоналей, А6 – середина А1А4 3. Докажите, что длина ломаной А1А2А3А4 больше длины ломаной А1А3А4

Домашнее задание § 13 П.113 №1,2