Презентация на тему: Ломаная , многоугольник и его виды

Ломаная , многоугольник и его виды. Выполнила:Мирабова ИринаУченица 9«И» класса.

Ломаная Ломаной A1A2... An называется фигура, которая состоит из упорядоченной совокупности точек и отрезков, соединяющих соседние среди них. Точки A1, A2, ... , An называются вершинами, а отрезки A1A2, A2A3, ... , An – 1An – звеньями ломаной. Звенья, имеющие общий конец, назовем смежными, а точки A1 и An – концами ломаной. Ломаная называется простой, если несмежные ее звенья не имеют общих точек. Ломаная называется замкнутой, если ее концы соединены отрезком. Этот отрезок также называется звеном, а концы ломаной считаются соседними вершинами.

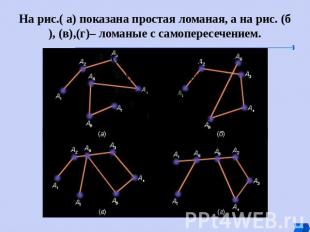
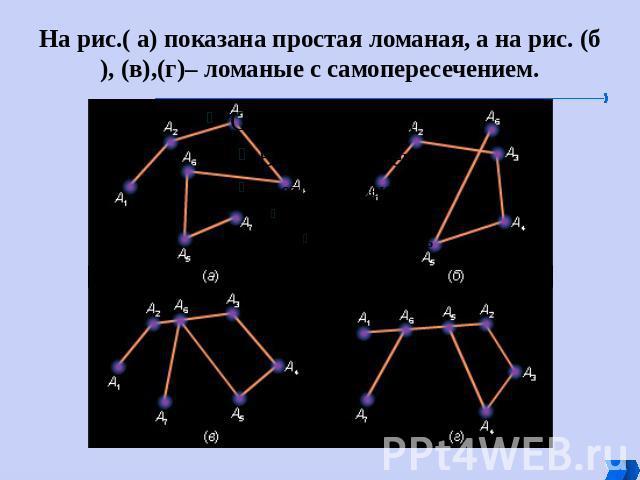
На рис.( а) показана простая ломаная, а на рис. (б), (в),(г)– ломаные с самопересечением.

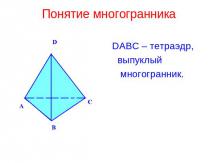
Многоугольник. МНОГОУГОЛЬНИК (на плоскости), геометрическая фигура, ограниченная замкнутой ломаной линией, звенья которой называются сторонами многоугольника, а их концы - вершинами многоугольника. По числу вершин различают треугольники, четырехугольники и т. д.

выпуклый, невыпуклый многоугольник. Многоугольник называют выпуклым, если выполнено одно из следующих условий: а) он лежит по одну сторону от любой из своих сторон (т. е. продолжения сторон многоугольника не пересекают других его сторон); б) он является пересечением (т. е. общей частью) нескольких полуплоскостей; в) любой отрезок с концами в точках, принадлежащих многоугольнику, целиком ему принадлежит. 2. Фигуру называют выпуклой, если любой отрезок с концами в точках фигуры целиком принадлежит ей.

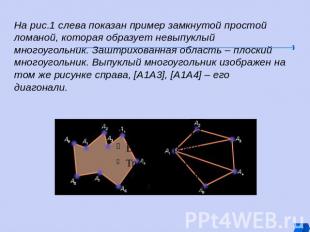
На рис.1 слева показан пример замкнутой простой ломаной, которая образует невыпуклый многоугольник. Заштрихованная область – плоский многоугольник. Выпуклый многоугольник изображен на том же рисунке справа, [A1A3], [A1A4] – его диагонали.

Количество диагоналей N у многоугольника легко вычислить по формуле: N = n·(n – 3)/2, где n — число вершин многоугольника. По этой формуле нетрудно найти, чтоу треугольника — 0 диагоналей у прямоугольника — 2 диагоналиу пятиугольника — 5 диагоналейу шестиугольника — 9 диагоналейу восьмиугольника — 20 диагоналейу 12-угольника — 54 диагоналиу 24-угольника — 252 диагонали

Сумма углов «выпуклого» n-угольника. Сумма углов выпуклого n-угольника равна (n-2)*180, где n - число углов данного многоугольника.

Сумма внешних углов «выпуклого »многоугольника. Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол это разность между 180° и внутренним углом, он может принимать значения от -180° до 180°.Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360°.Формула: 180° *n-180° *(n-2)=360°

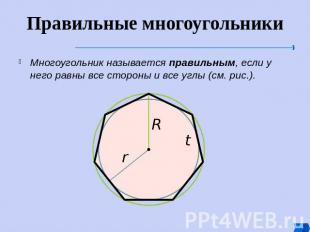
Правильные многоугольники Многоугольник называется правильным, если у него равны все стороны и все углы (см. рис.).

Что бы определить число сторон «правильного» n-уголька нужно воспользоваться формулой. a*n=180° *n-360° отсюда следует,360°=180°n-a°n

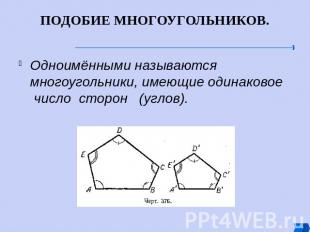
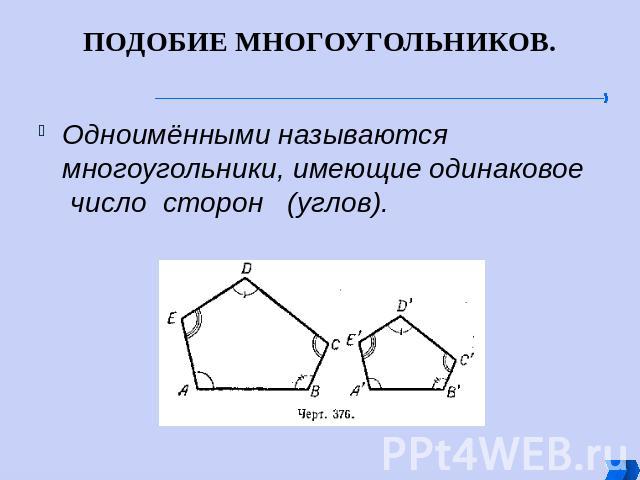
ПОДОБИЕ МНОГОУГОЛЬНИКОВ. Одноимёнными называются многоугольники, имеющие одинаковое  число  сторон   (углов).