Презентация на тему: Длина окружности (9 класс)

Длина окружности Геометрия. 9 класс.

Мастер подключения презентации к уроку. S T O P Дальнейший просмотр возможен только при наличии соответствующих знаний. А они у тебя есть?

Понятие длины окружности. Представим себе нить в форме окружности. Разрежем её и растянем за концы. Длина полученного отрезка и есть длина окружности.

Периметр любого вписанного в окружность многоугольника является приближённым значением длины окружности. При увеличении числа сторон правильный многоугольник всё ближе и ближе «прилегает» к окружности. Длина окружности – это предел, к которому стремится периметр правильного вписанного многоугольника при неограниченном увеличении числа его сторон.

Свойство длины окружности. Отношение длины окружности к её диаметру есть одно и то же число для всех окружностей. ( стр. 265, курсив предпоследний абзац) Дано: Окр(О1;R1),Oкр(O2;R2), C1 – длина Oкр(O1; R1), C2 – длина Oкр(O2; R2). Доказать:

Доказательство: 1) Впишем в каждую окружность правильный n-угольник. Пусть Р1, Р2 – их периметры; а аn1, an2 – их стороны. Тогда P1= n.an1= Если число сторон неограниченно увеличивать, то n , По свойству пропорции

Число «пи». Вывод формулы длины окружности. Из свойства длины окружности следует . что есть число постоянное и теоретически доказано, что это число иррациональное. Обозначают его греческой буквой «пи». Это я знаю и помню прекрасно.

Задача 1. Вообразите, что вы обошли землю по экватору. На сколько при этом верхушка вашей головы прошла более длинный путь, чем кончик вашей ноги? Решение. Ноги прошли путь , где R радиус земного шара. Верхушка головы - где 1,7м рост человека. Разность путей равна Итак голова прошла путь на 10,7 м больше, чем ноги.

Задача 2. Если обтянуть земной шар по экватору проволокой и затем прибавить к её длине 1м, то сможет ли между проволокой и землёй проскочить мышь.Обычно отвечают, что промежуток будет тоньше волоса. Решение. Пусть длина промежутка х см. Если R радиус земли, то длина проволоки была 2Rсм, а станет 2 (R + x)см. А по условию задачи их разность равна 100 см.

№ 1104(а). Найти длину окружности описанной около правильного треугольника со стороной а. Выразите R через а. Подставьте в формулу длины окружности.

№ 1104 (в). Найти длину окружности описанной около равнобедренного треугольника с основа Найти: С. нием а и

№ 1104 (в). Найти длину окружности описанной около равнобедренного треугольника с основанием а и боковой стороной b.

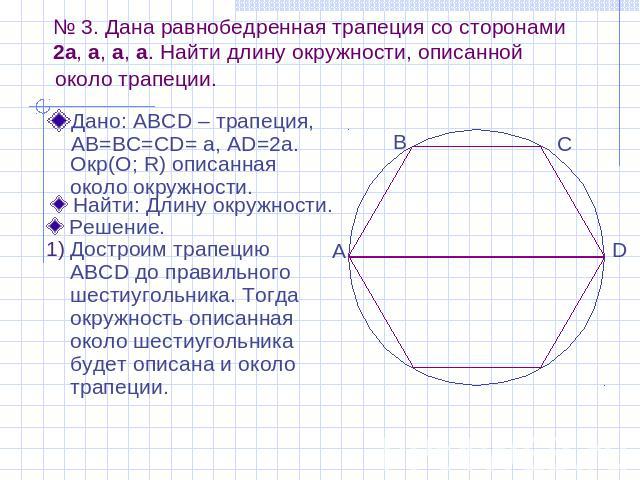
№ 3. Дана равнобедренная трапеция со сторонами 2a, a, a, a. Найти длину окружности, описанной около трапеции. Дано: АВСD – трапеция, АВ=ВС=СD= а, АD=2а. Окр(О; R) описанная около окружности. Найти: Длину окружности. Решение. Достроим трапецию ABCD до правильного шестиугольника. Тогда окружность описанная около шестиугольника будет описана и около трапеции.

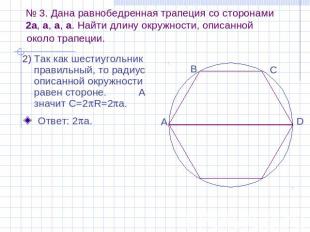
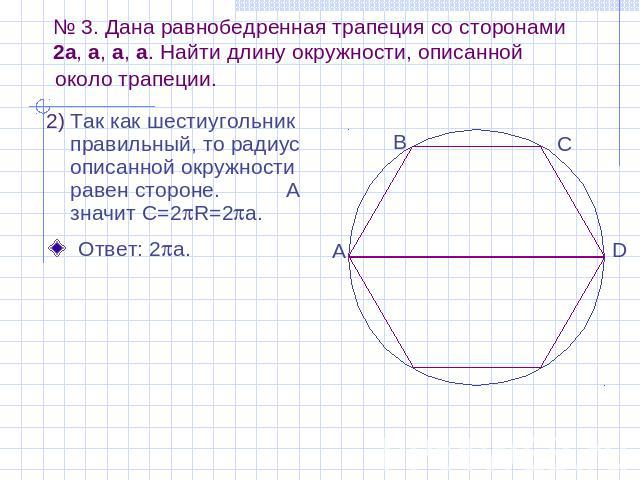
№ 3. Дана равнобедренная трапеция со сторонами 2a, a, a, a. Найти длину окружности, описанной около трапеции. Так как шестиугольник правильный, то радиус описанной окружности равен стороне. А значит C=2R=2a.

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ Сформулируйте основное свойство длины окружности. На чём основывается его доказательство? Как вычисляется длина окружности по формуле? Какое число обозначается буквой и чему равно его приближённое значение? Как изменится длина окружности, если радиус окружности уменьшить (увеличить) в k раз? Как изменится длина окружности, если радиус окружности уменьшить (увеличить) в k раз?

Домашнее задание     Вопросы 8-9(стр. 270).     №1108, №1105(а).

Спасибо за урок, дети.