Презентация на тему: Векторы

Векторы Геометрия 9 класс

Оглавление Понятие вектора Длина вектора Коллинеарные вектора Сонаправленные вектора Противоположно направленные вектора Равенство векторов Сложение векторов Правило треугольника Правило параллелограмма Сложение нескольких векторов Вычитание векторов Произведение вектора на число

Понятие вектора Многие физические величины характеризуются числовым значением и направлением в пространстве, их называют векторными величинами

Понятие вектора Отрезок, для которого указано, какая его граничная точка является началом, а какая - концом, называется направленным отрезком или вектором

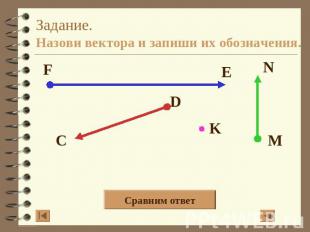
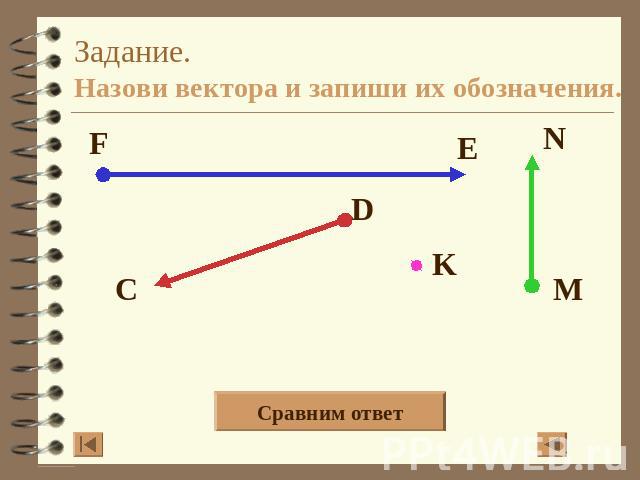
Задание.Назови вектора и запиши их обозначения.

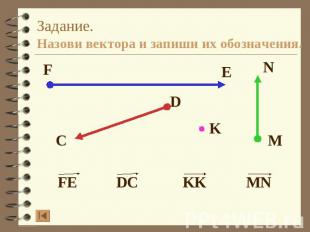
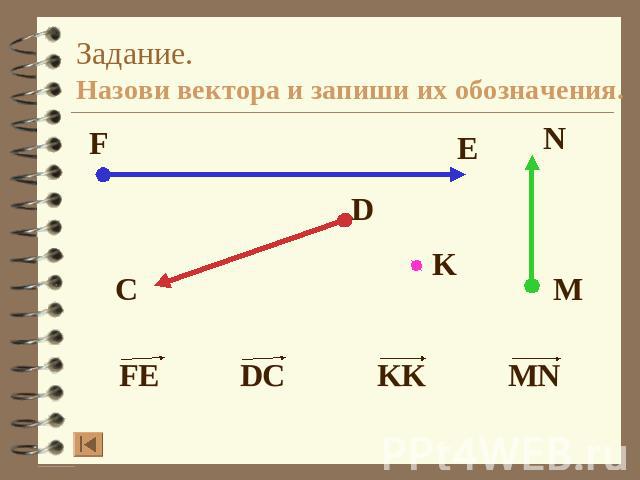
Задание.Назови вектора и запиши их обозначения.

Длина вектора вектор MN или вектор а Длиной вектора или модулем не нулевого вектора называется длина отрезка |MN| = |a| длина вектора MN вектор КК или нулевой вектор

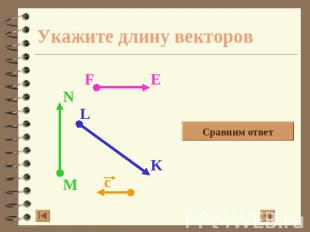
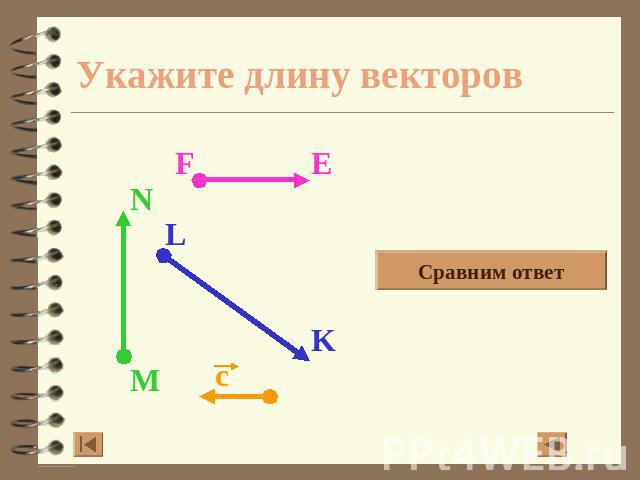
Укажите длину векторов

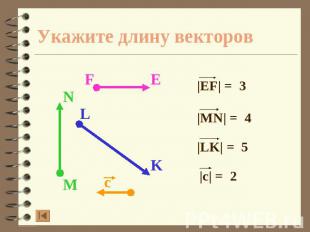
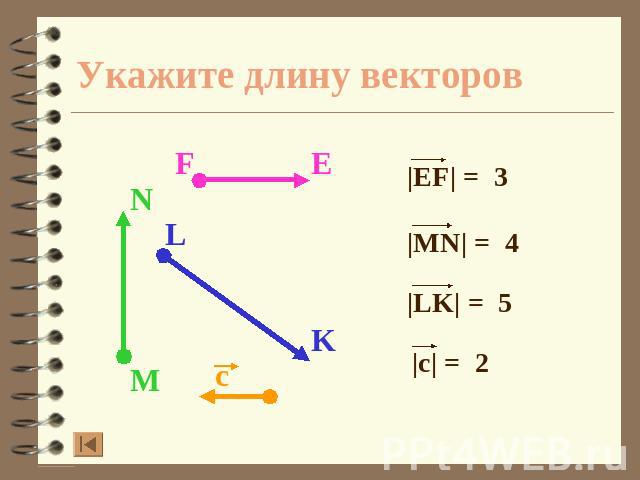
Укажите длину векторов

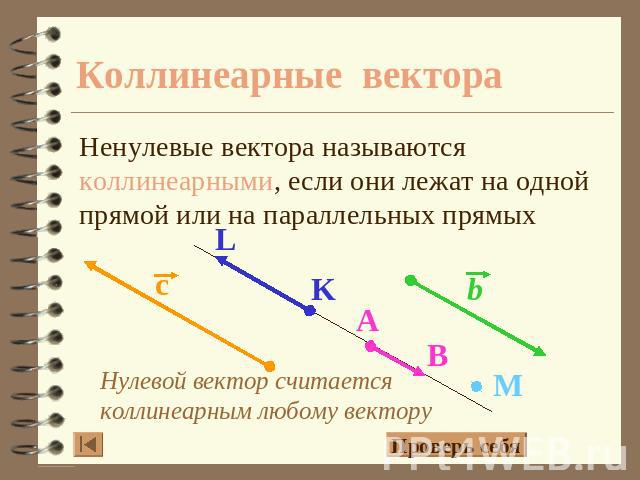
Коллинеарные вектора Ненулевые вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых Нулевой вектор считается коллинеарным любому вектору

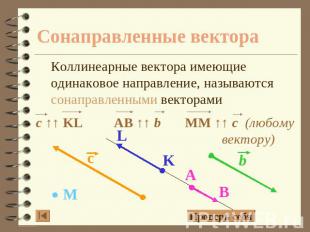
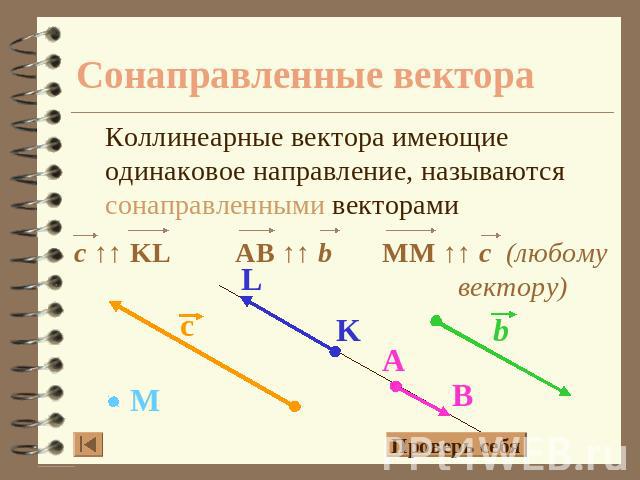
Сонаправленные вектора Коллинеарные вектора имеющие одинаковое направление, называются сонаправленными векторами

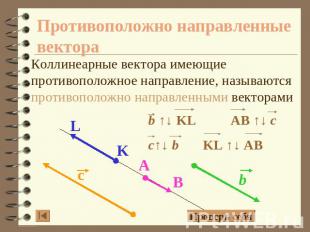
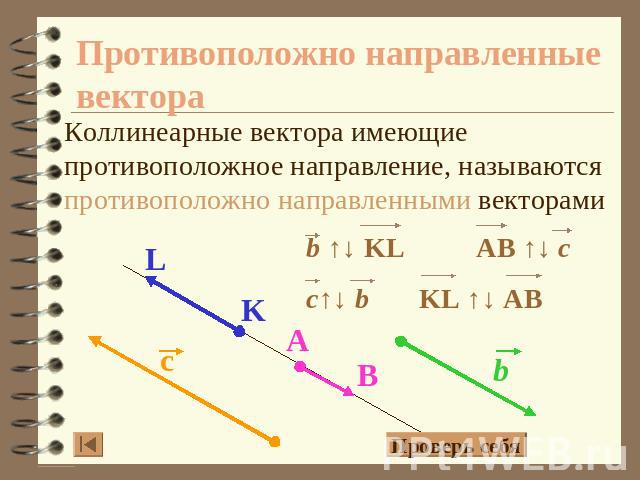
Противоположно направленные вектора Коллинеарные вектора имеющие противоположное направление, называются противоположно направленными векторами

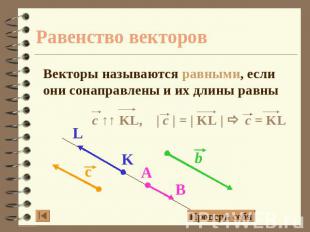
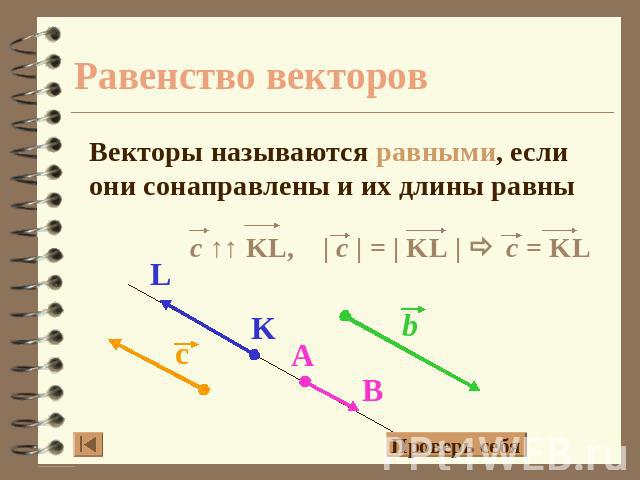
Равенство векторов Векторы называются равными, если они сонаправлены и их длины равны

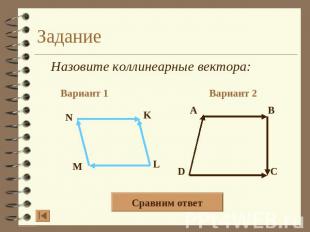
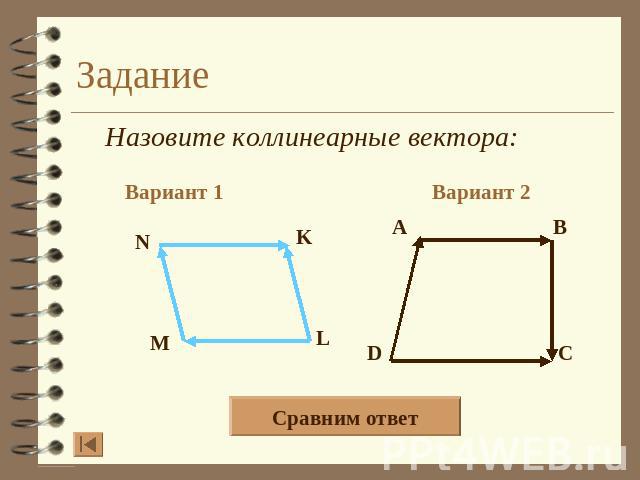
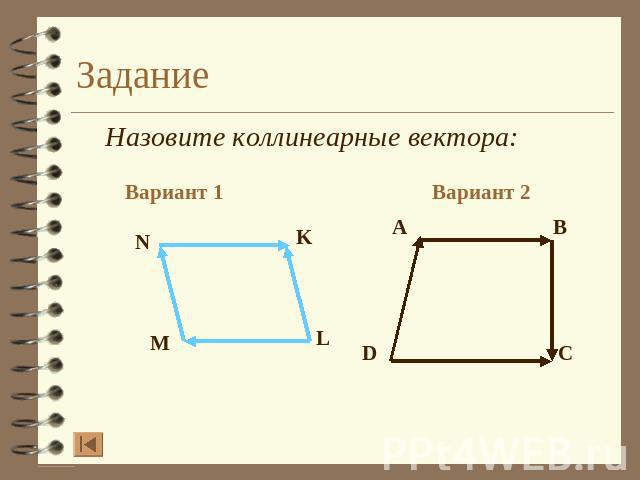
Задание Назовите коллинеарные вектора:

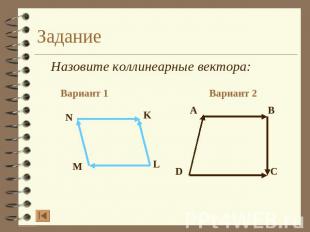
Задание Назовите коллинеарные вектора:

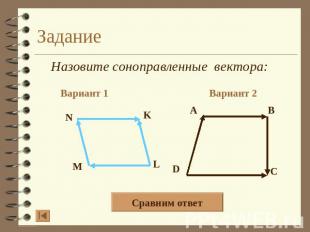
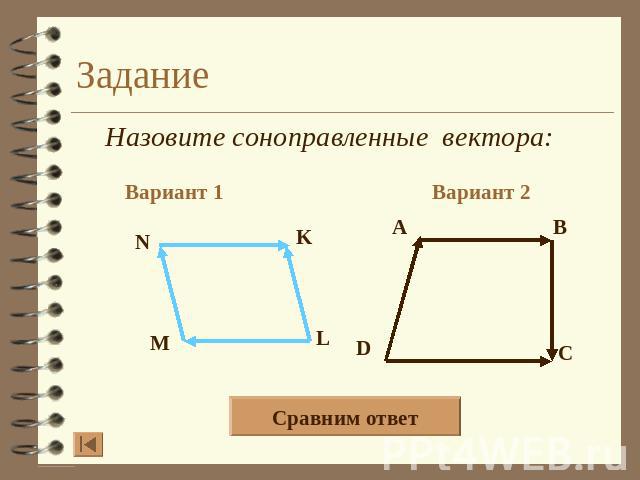
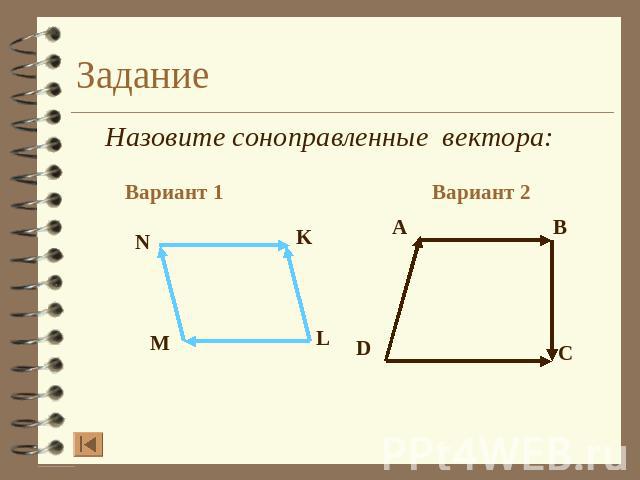
Задание Назовите соноправленные вектора:

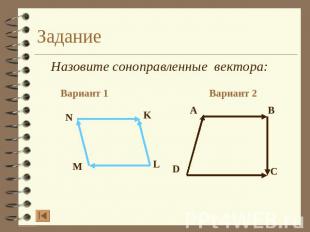
Задание Назовите соноправленные вектора:

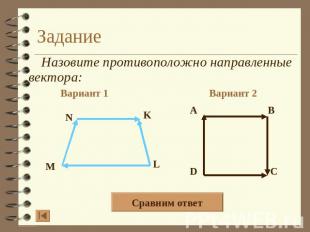
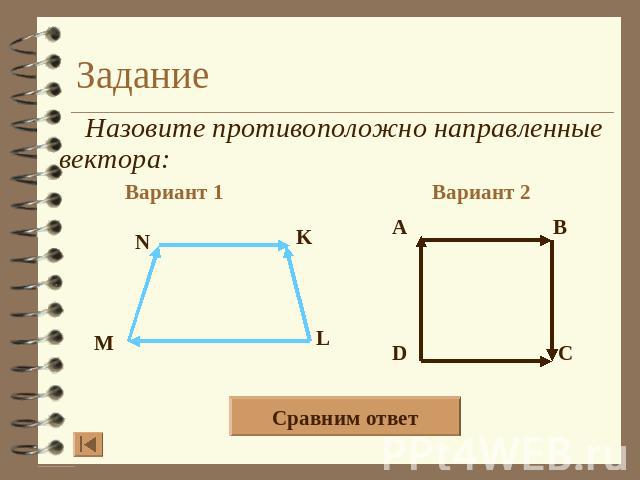
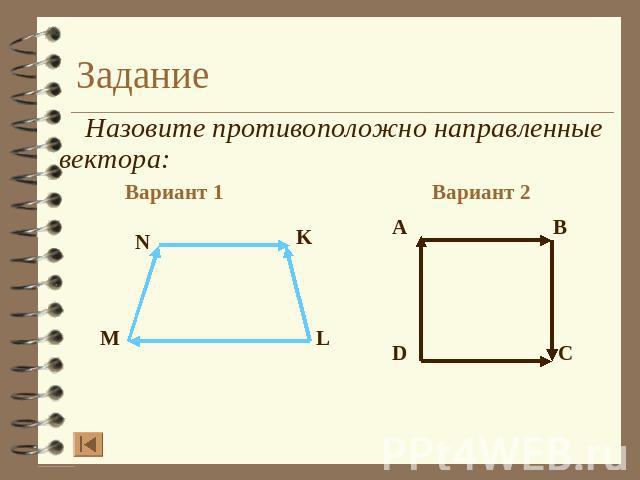
Задание Назовите противоположно направленные вектора:

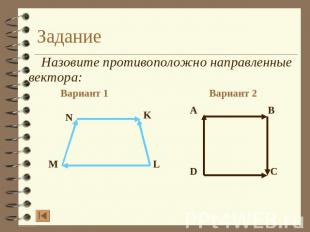
Задание Назовите противоположно направленные вектора:

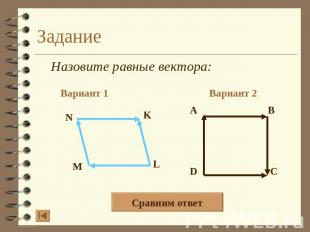
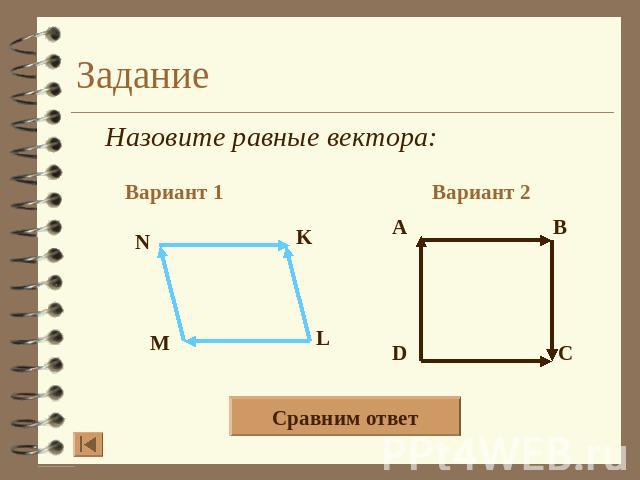
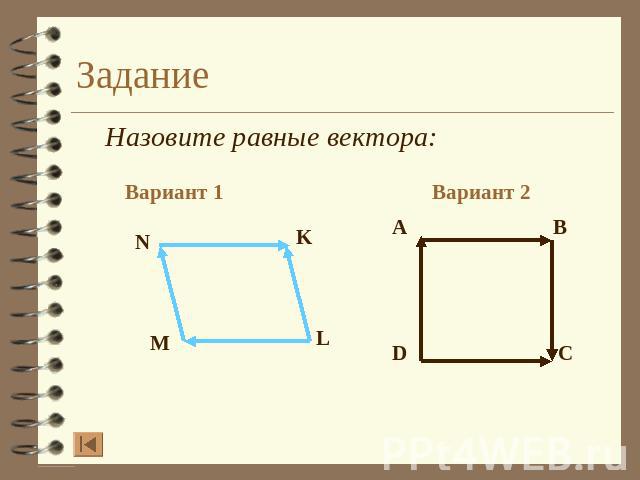
Задание Назовите равные вектора:

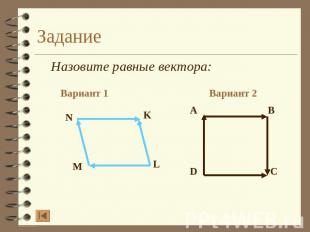
Задание Назовите равные вектора:

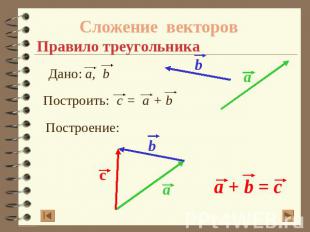
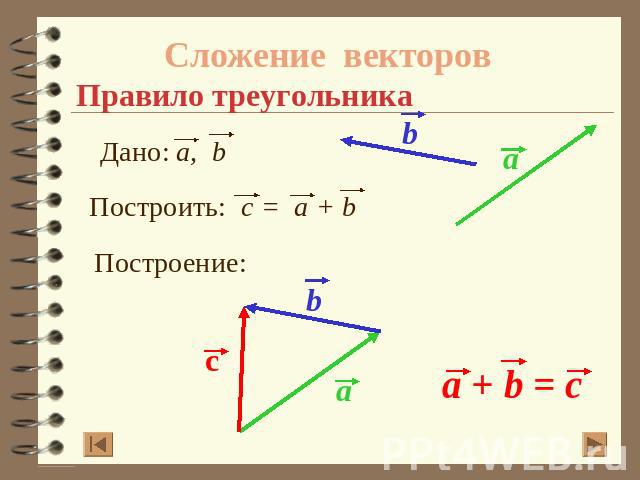
Сложение векторовПравило треугольника

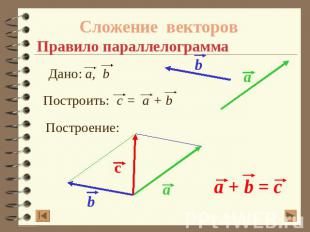
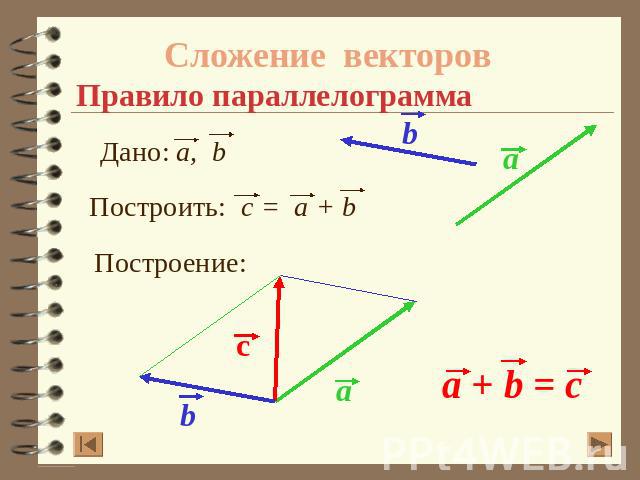
Сложение векторовПравило параллелограмма

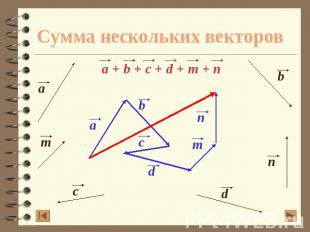
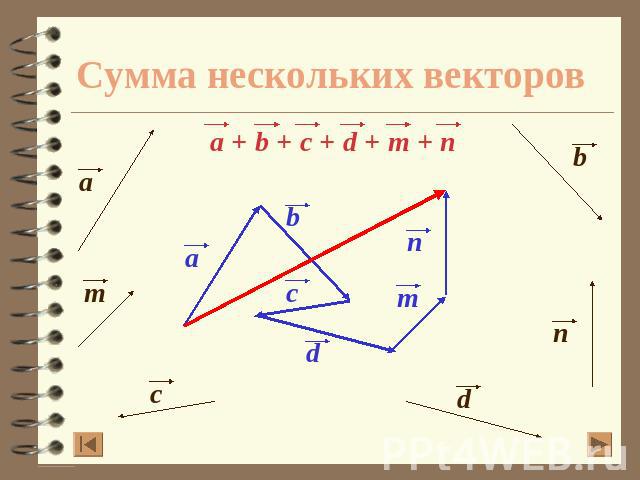
Сумма нескольких векторов

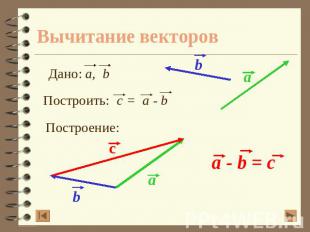
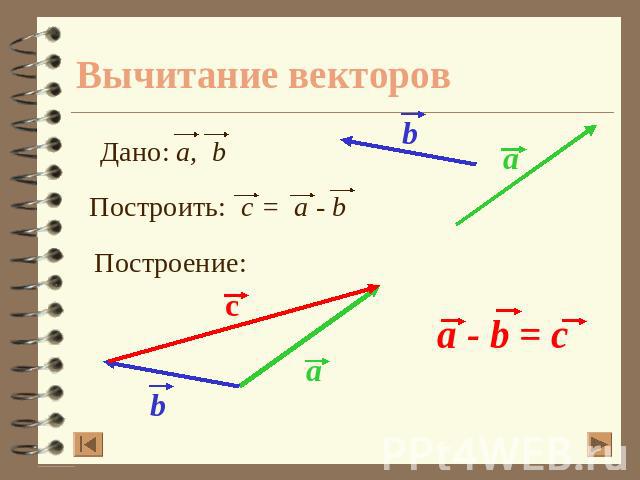
Вычитание векторов

Умножение вектора a на число k k·a = b, |a| ≠ 0, k – произвольное число |b| = |k|·|a|, если k>0, то a ↑↑ b если k<0, то a ↑↓ b Для любых чисел k, l и любых векторов a, b справедливы равенства: 1º. (kl)a= k(la) (сочетательный закон), 2º. (k+l)a= ka+la (первый распределительный закон), 3º. k(a+b) = ka+kb (второй распределительный закон).