Презентация на тему: Векторы в пространстве

Векторы в пространстве Понятие вектора в пространстве Сложение и вычитание векторов Умножение вектора на число Компланарные векторы

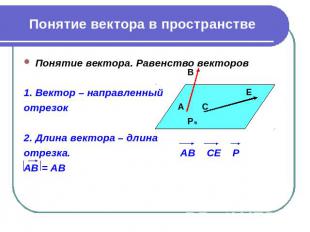
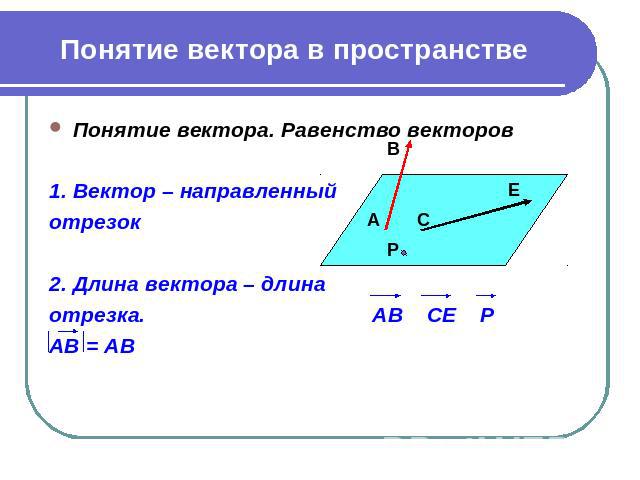
Понятие вектора в пространстве Понятие вектора. Равенство векторов 1. Вектор – направленный отрезок 2. Длина вектора – длина отрезка. АВ СЕ Р АВ = АВ

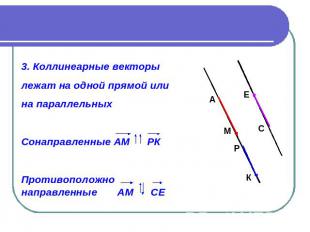
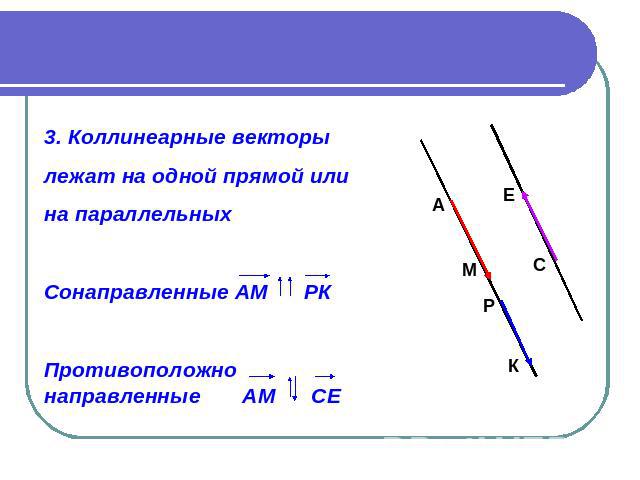
3. Коллинеарные векторы лежат на одной прямой или на параллельных Сонаправленные АМ РК Противоположно направленные АМ СЕ

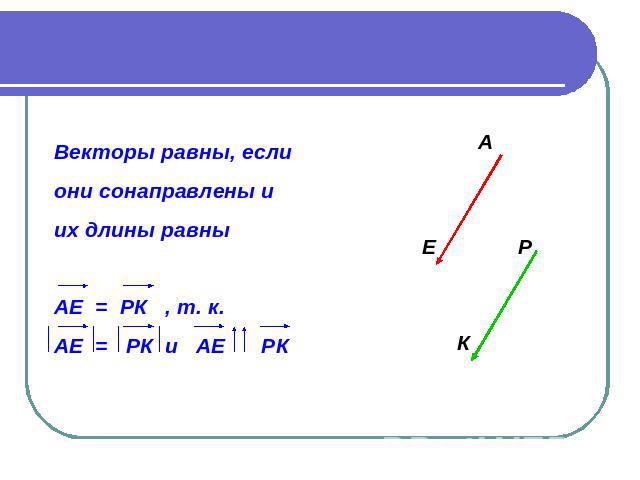
Векторы равны, если они сонаправлены и их длины равны АЕ = РК , т. к. АЕ = РК и АЕ РК

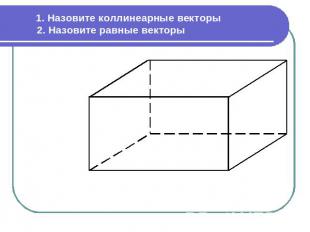
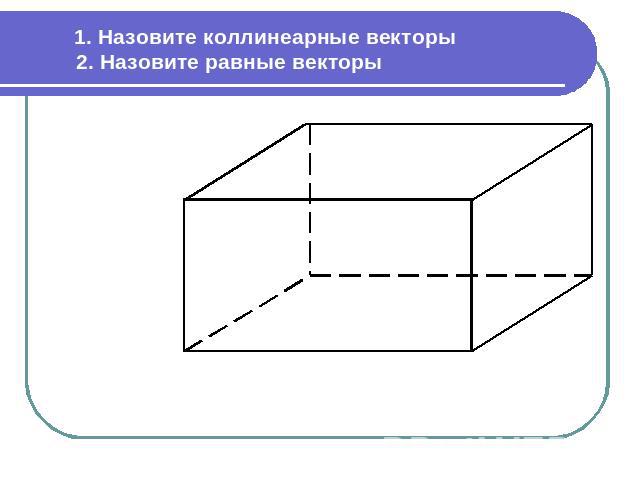
1. Назовите коллинеарные векторы 2. Назовите равные векторы

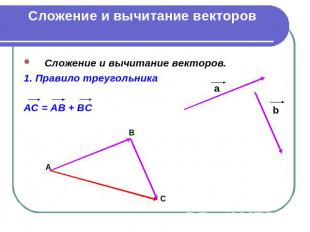
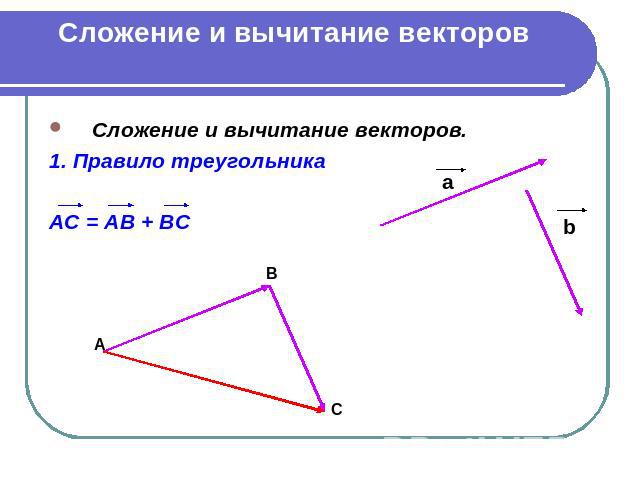
Сложение и вычитание векторов Сложение и вычитание векторов. 1. Правило треугольника АС = АВ + ВС

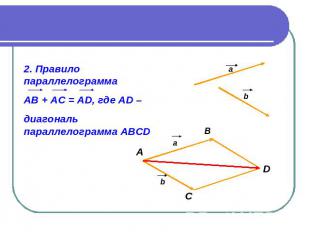
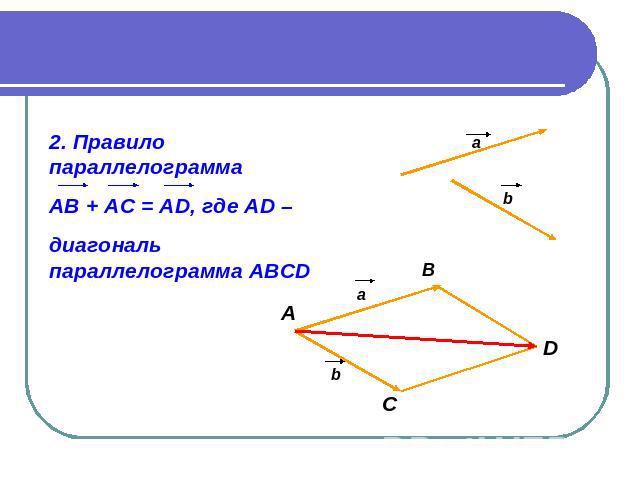
2. Правило параллелограмма АВ + АС = АD, где АD – диагональ параллелограмма АВСD

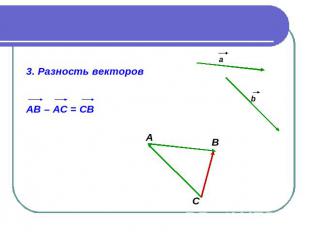
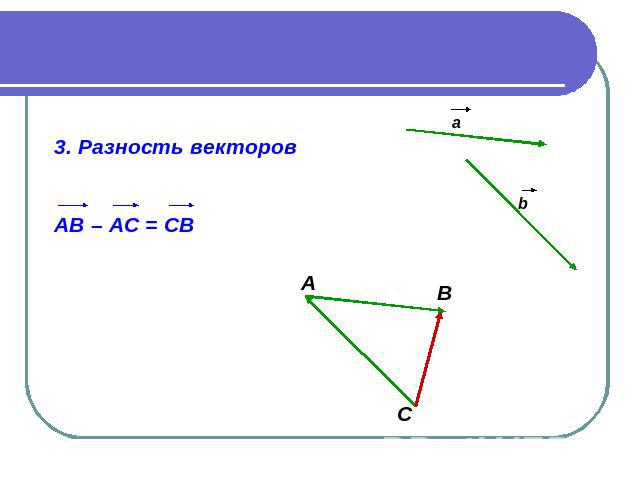
3. Разность векторов АВ – АС = СВ

Умножение вектора на число b = k a, если b = k a если k > 0, то a b если k < 0, то a b

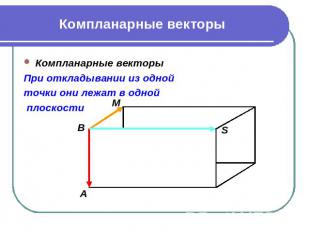
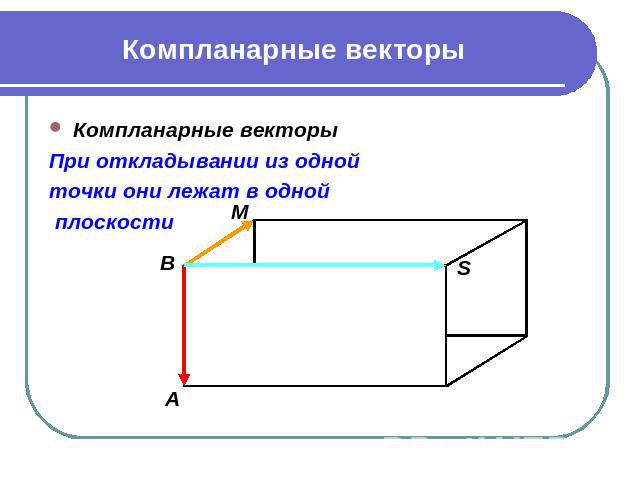
Компланарные векторы Компланарные векторы При откладывании из одной точки они лежат в одной плоскости

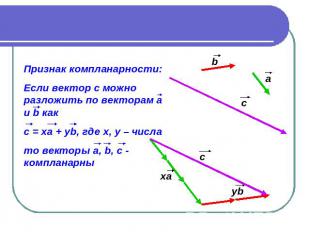
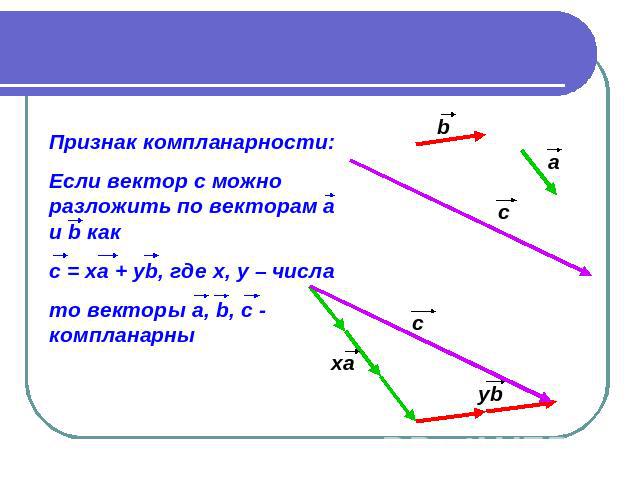
Признак компланарности: Если вектор с можно разложить по векторам а и b как c = xa + yb, где x, y – числа то векторы a, b, c - компланарны

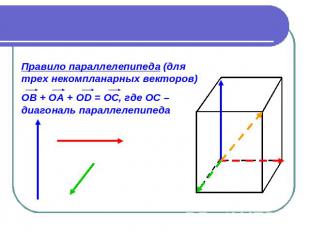
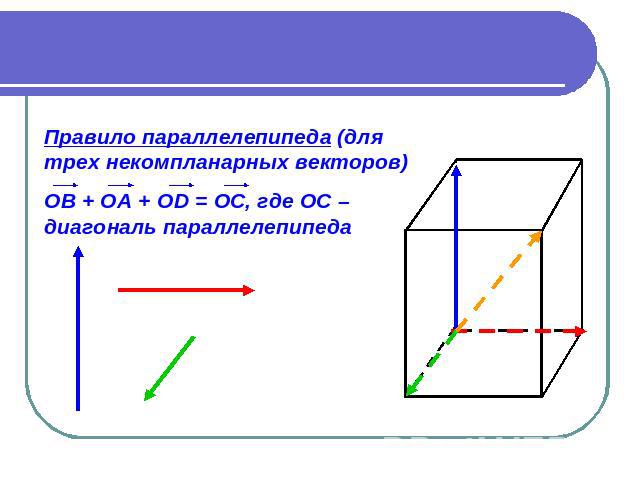
Правило параллелепипеда (для трех некомпланарных векторов) ОВ + ОА + ОD = ОС, где ОС – диагональ параллелепипеда