Презентация на тему: Векторы в пространстве

Проект на тему:Векторы в пространстве. Выполнил ученик 11 класса Юдин Владимир Учитель математики Стрельникова Л.П.

Прямоугольная система координат. Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для обеих осей.

Направление осейПоложительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° еe положительное направление совпало с положительным направлением оси OY. Четыре угла (I, II, III, IV), образованные осями координат OX и OY, называются координатными углами.

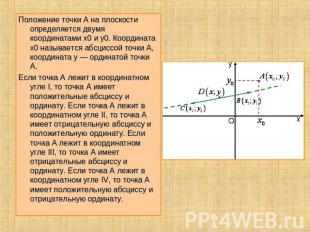
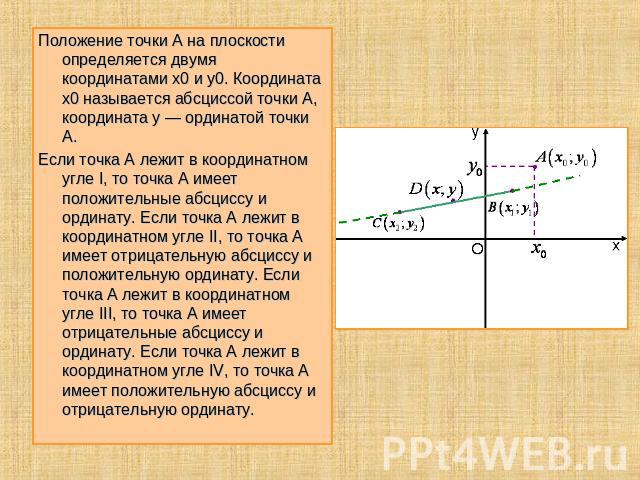
Положение точки A на плоскости определяется двумя координатами x0 и y0. Координата x0 называется абсциссой точки A, координата y — ординатой точки A.Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.

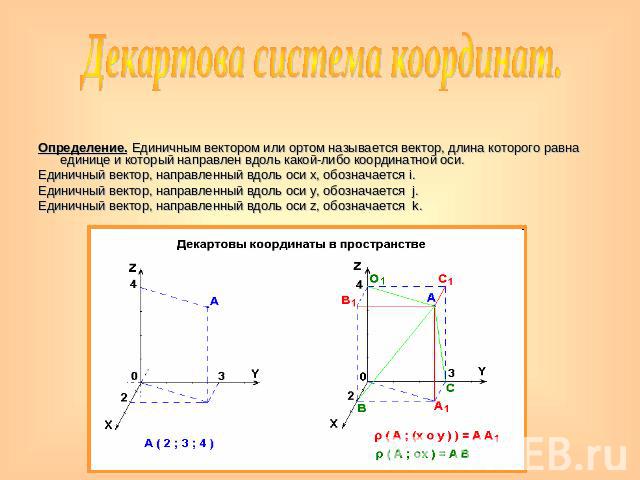
Уравнение окружности.Уравнение окружности с центром в начале координат: x2 + y2 = R2Уравнение окружности с центром в точке (x0;y0) : (x - x0)2 + (y - y0)2 = R2Прямые x, y, z называются координатными осями (или осями координат), точка их пересечения O – началом координат, а плоскости xOy, xOz и yOz – координатными плоскостями. Точка O разбивает каждую координатную ось на две полупрямые, которые называются положительной и отрицательной полуосями. Координатой точки A по оси x будем называть число, равное по абсолютной величине длине отрезка OAx: положительное, если точка A лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси. Аналогично можно определить координаты y и z точки A. Координаты точки A записываются в скобках рядом с названием этой точки: A (x; y; z).

Декартова система координат.Определение. Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси. Единичный вектор, направленный вдоль оси x, обозначается i. Единичный вектор, направленный вдоль оси y, обозначается j. Единичный вектор, направленный вдоль оси z, обозначается k.

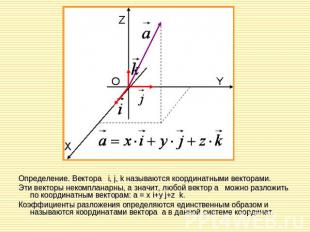
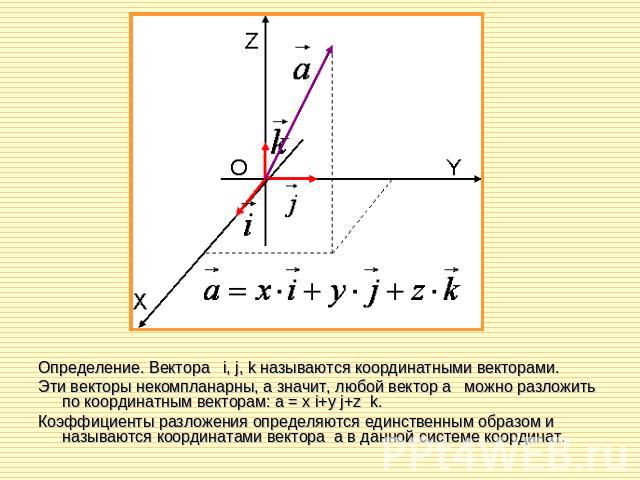
Определение. Вектора i, j, k называются координатными векторами. Эти векторы некомпланарны, а значит, любой вектор a можно разложить по координатным векторам: a = x i+y j+z k.Коэффициенты разложения определяются единственным образом и называются координатами вектора a в данной системе координат.

Свойства векторов.Свойства векторов, заданных координатами Координаты нулевого вектора равны нулю. Координаты равных векторов соответственно равны. Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов. Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов. Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число.

Условие перпендикулярности векторов.Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.Даны два вектора a(x_{a}; y_{a}) и b(x_{b}; y_{b}). Эти векторы будут перпендикулярны, если выражение xaxb + yayb = 0.Условие коллинеарности векторовВекторы коллинеарны, если абсцисса первого вектора относится к абсциссе второго так же, как ордината первого — к ординате второго.Даны два вектора a(x_{a}; y_{a}) и b(x_{b}; y_{b}). Эти векторы коллинеарны, если xa = λ xb и ya = λ yb, где λ=R.

Конец!