Презентация на тему: Векторы в пространстве как система геометрии

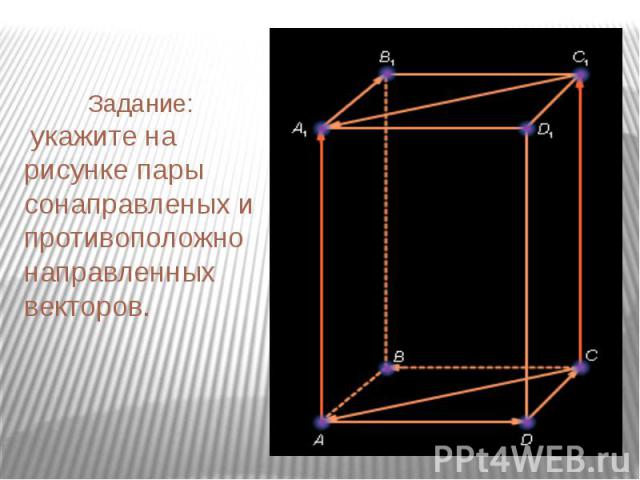
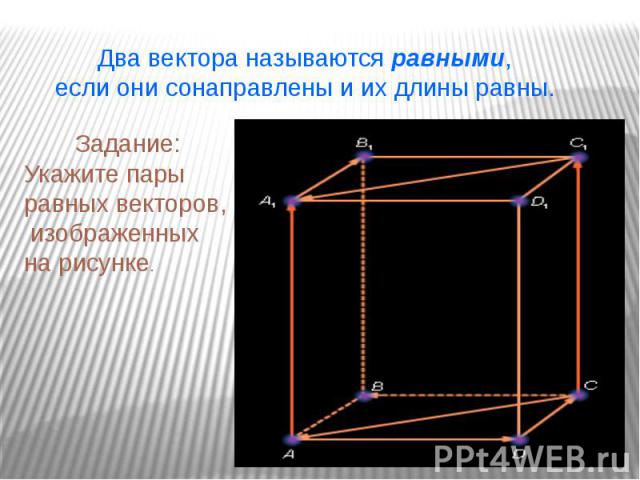
Геометрия-10 учитель: Текеева З.М. Векторы в пространстве

Вектор – направленный отрезок. Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а какой концом. На рисунках направление вектора обозначается стрелкой от начала к концу. Если длина рассматриваемого отрезка равна нулю, то есть отрезок вырождается в точку, то эта точка тоже может рассматриваться как вектор. Такой вектор называется нулевым и имеет произвольное направление.

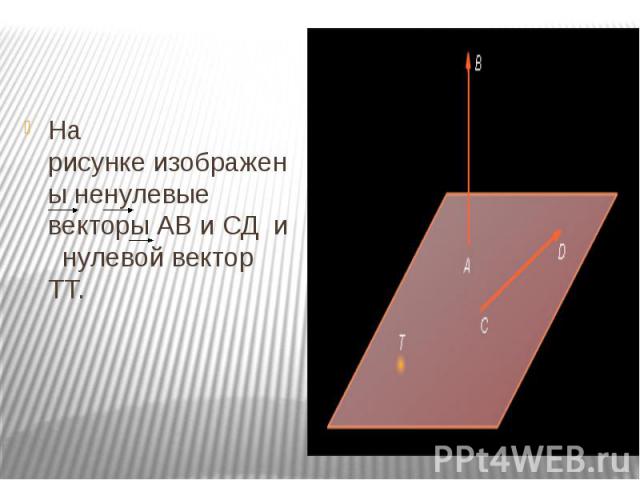
На рисунке изображены ненулевые векторы АВ и СД и нулевой вектор ТТ. На рисунке изображены ненулевые векторы АВ и СД и нулевой вектор ТТ.

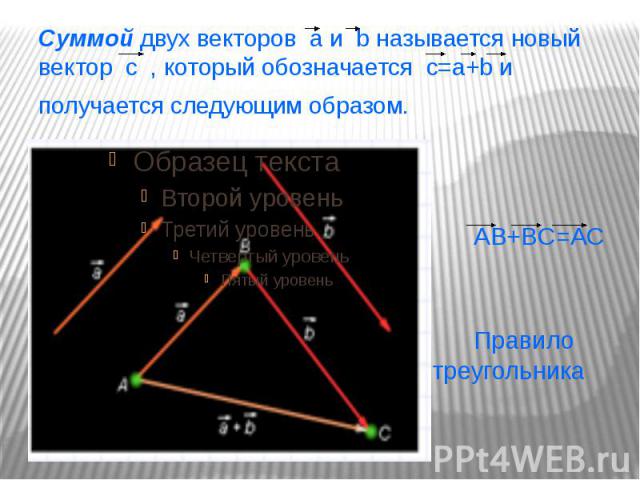
Суммой двух векторов а и b называется новый вектор c , который обозначается c=a+b и получается следующим образом. AB+BC=AC Правило треугольника

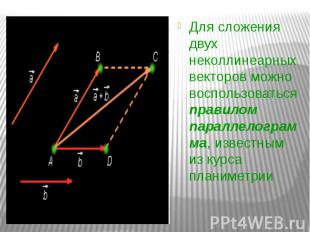
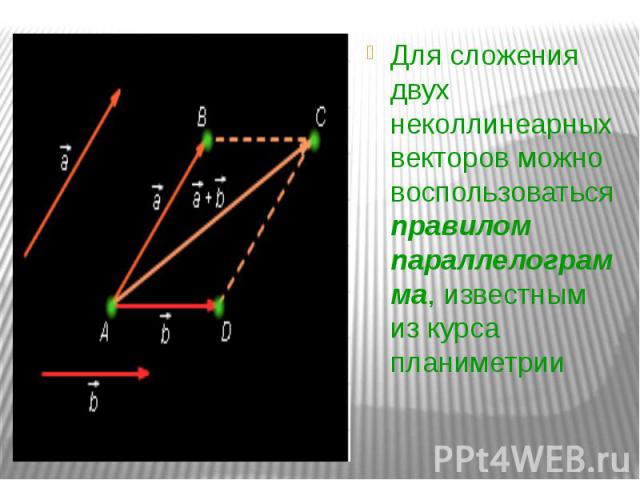
Для сложения двух неколлинеарных векторов можно воспользоваться правилом параллелограмма, известным из курса планиметрии Для сложения двух неколлинеарных векторов можно воспользоваться правилом параллелограмма, известным из курса планиметрии

Законы сложения векторов

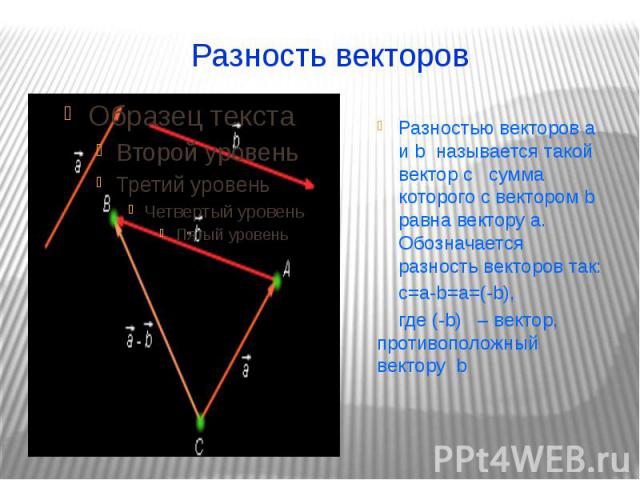
Разность векторов Разностью векторов a и b называется такой вектор c сумма которого с вектором b равна вектору a. Обозначается разность векторов так: c=a-b=a=(-b), где (-b) – вектор, противоположный вектору b

Умножение вектора на число Произведением ненулевого вектора a на число k называется вектор b длина которого равна |k| |a| причем при k > 0 векторы a и ka сонаправлены, а при k < 0 – противоположно направлены. Произведением любого числа на нулевой вектор является нулевой вектор. Из определения следует, что векторы a и ka коллинеарны. Кроме того, произведение любого вектора на число 0 есть нулевой вектор.

ЗАКОНЫ УМНОЖЕНИЯ ВЕКТОРА НА ЧИСЛО