Презентация на тему: Площади многоугольников и их свойства

Тема урока Площади многоугольников

Понятие площади Что принимают за единицу измерения площади? В каких единицах измеряется площадь? Чем выражается площадь многоугольника, что показывает это число?

Свойства площадей Равные многоугольники имеют равные площади Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников Площадь квадрата равна квадрату его стороны

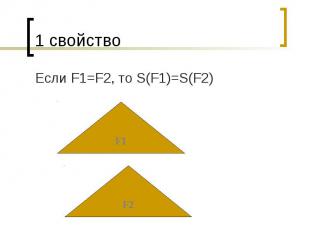
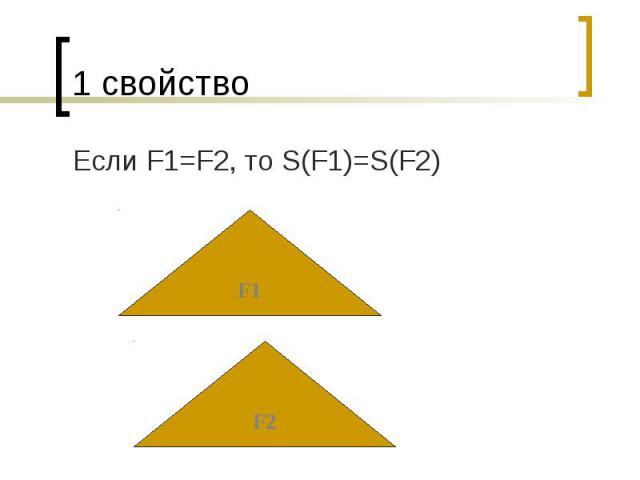
1 свойство Если F1=F2, то S(F1)=S(F2)

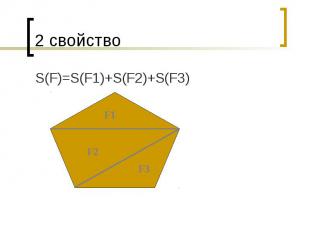
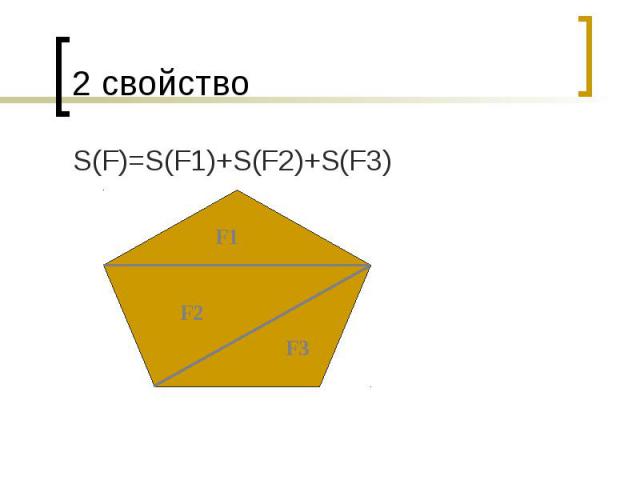
2 свойство S(F)=S(F1)+S(F2)+S(F3)

3 свойство Sкв=a2

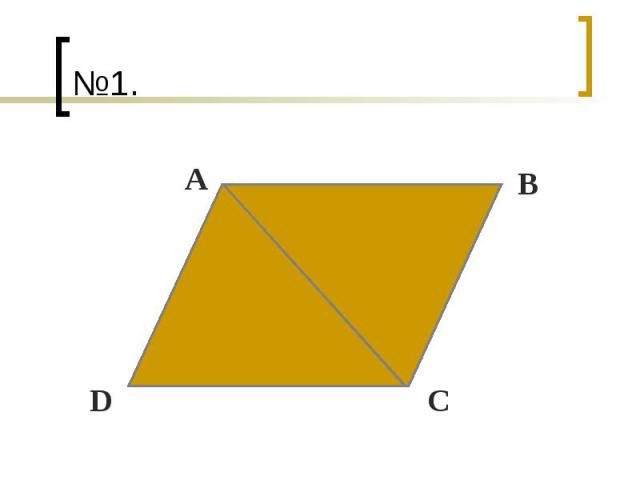
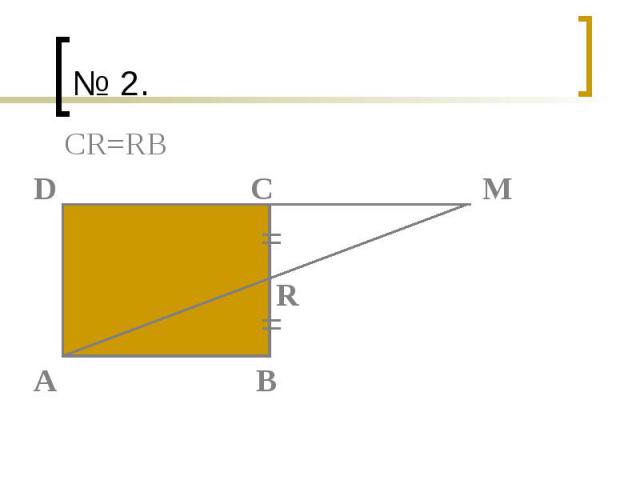
Задачи Площадь параллелограмма ABCD равна S. Найдите площади треугольников ABC и ABD. Площадь прямоугольника ABCD равна Q. Найдите площадь треугольника AMD. Заполните таблицу, где S – площадь квадрата, а – сторона квадрата.

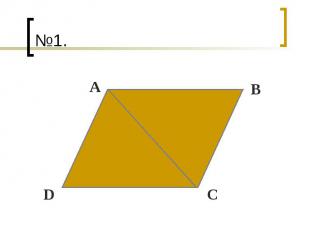
№1.

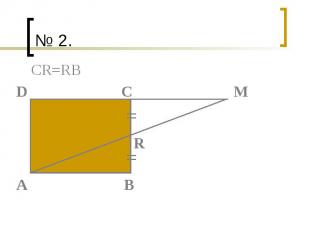
№ 2.

№ 3.

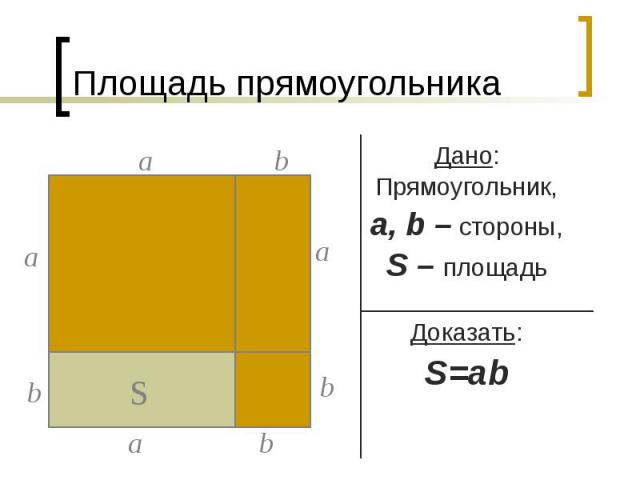
Площадь прямоугольника Теорема. Площадь прямоугольника равна произведению его смежных сторон.

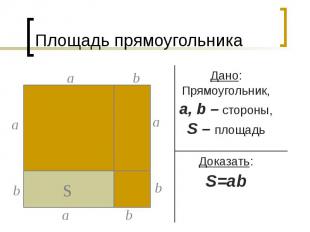
Площадь прямоугольника Дано: Прямоугольник, a, b – стороны, S – площадь Доказать: S=ab

Площадь прямоугольника Доказательство: По 3-му свойству площадь получившегося квадрата равна (а+b)2. По 2-му свойству имеем: (а+b)2= S+S+а2+b2 а2 +2аb+b2= 2S+а2+b2 Отсюда получаем: S=ab