Презентация на тему: Правильные многогранники и их приметы

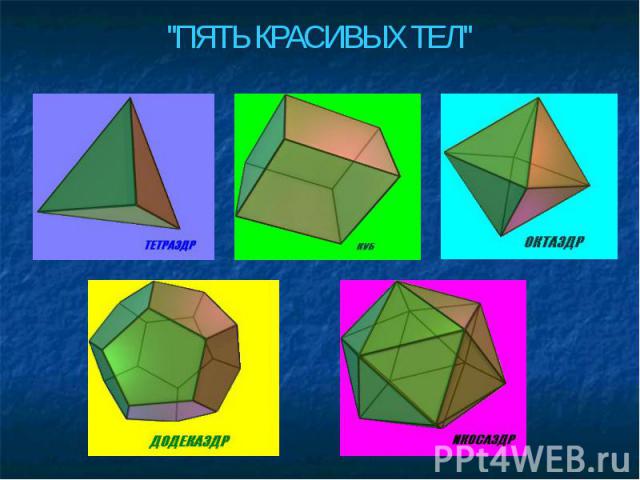
Тема: «Правильные многогранники» Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэролл

Многогранник называется правильным если:

1) ОН ВЫПУКЛЫЙ (Т.Е. ЛЕЖИТ ПО ОДНУ СТОРОНУ ОТ ПЛОСКОСТИ КАЖДОЙ ГРАНИ)

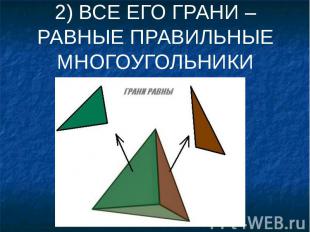
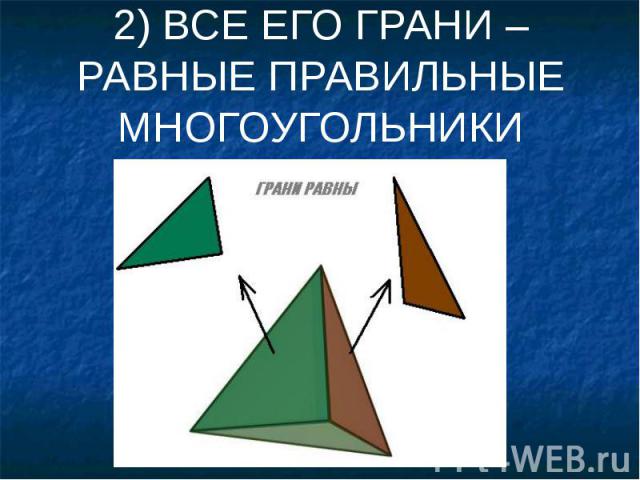
2) ВСЕ ЕГО ГРАНИ – РАВНЫЕ ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ

3) В КАЖДОЙ ЕГО ВЕРШИНЕ СХОДИТСЯ ОДИНАКОВОЕ ЧИСЛО ГРАНЕЙ

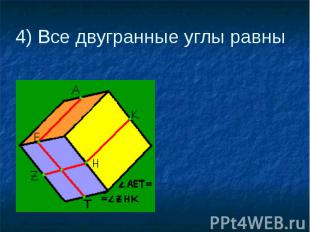
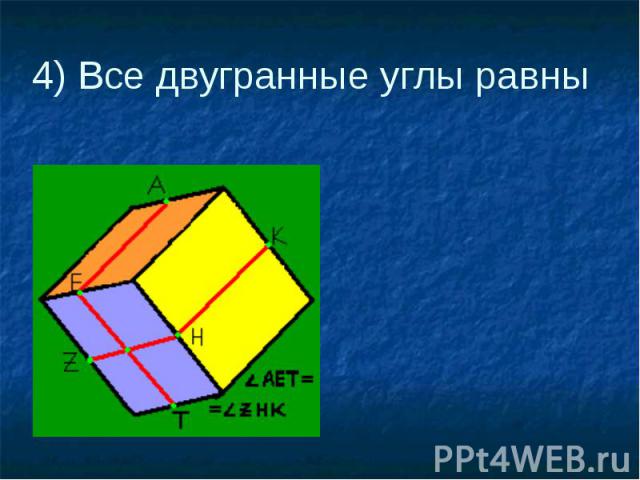
4) Все двугранные углы равны

Сколько же существует видов правильных многогранников? Грань - правильный треугольник n – внутренний угол правильного n – угольника = 60° n – число граней многогранного угла n = 3 60° · 3 = 180° < 360° n = 4 60° · 4 = 240° < 360° n = 5 60° · 5 = 300° < 360° n = 6 60° · 6 = 360° (многогранный угол совпадает с плоскостью) Существует три вида правильных многогранников, гранями которых являются правильные треугольники

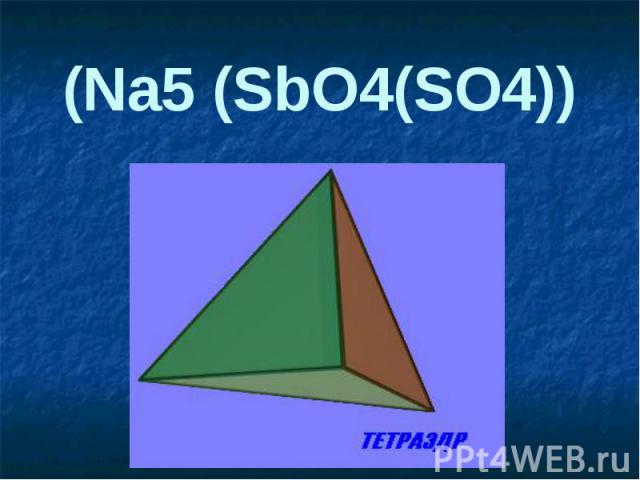
Правильный тетраэдр Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180º.

Правильный октаэдр

Правильный икосаэдр Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300º.

Грань – квадрат = 90° n – число граней многогранного угла n = 3 90° · 3 = 270° < 360° n = 4 90° · 4 = 360° (многогранный угол совпадает с плоскостью) Существует только один вид правильного многогранника, гранями которого являются квадраты

Куб (гексаэдр) Составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270º.

Грань – правильный пятиугольник

Правильный додекаэдр Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324º.

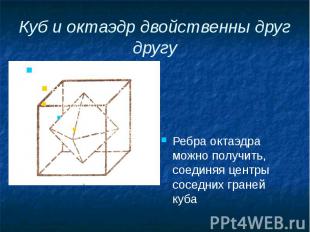
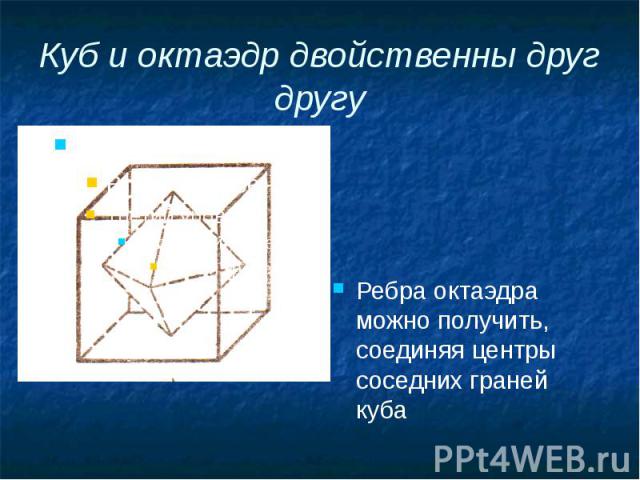
Куб и октаэдр двойственны друг другу Ребра октаэдра можно получить, соединяя центры соседних граней куба

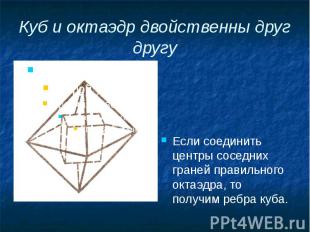
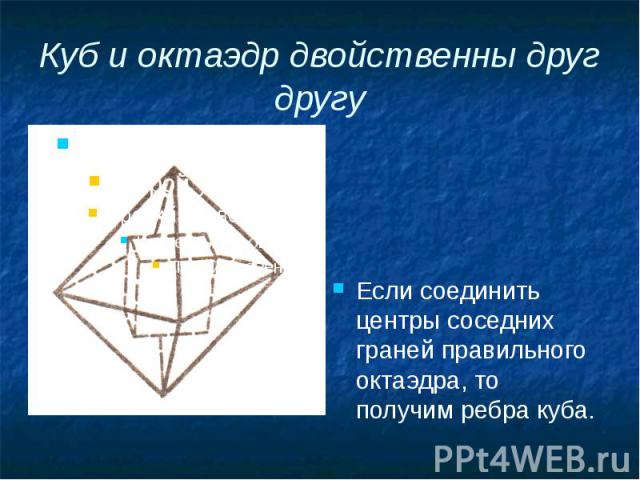
Куб и октаэдр двойственны друг другу Если соединить центры соседних граней правильного октаэдра, то получим ребра куба.

Додекаэдр и икосаэдр двойственны друг другу Если соединить отрезками центры соседних граней додекаэдра, то получим ребра икосаэдра

Додекаэдр и икосаэдр двойственны друг другу Если соединить отрезками центры соседних граней икосаэдра, то получим ребра додекаэдра

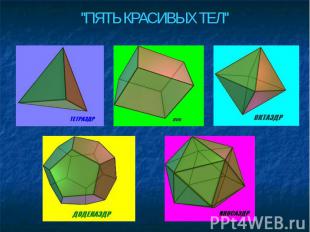
Рассматривая эту таблицу, Декарт в 1640 году подметил закономерность, а в 1752 году Эйлер сформулировал её в закон.

Г+В=Р+2, где Г - число граней В - число вершин Р - число рёбер

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ НАШЛИ СВОЁ ПРИМЕНЕНИЕ В СТРОИТЕЛЬНЫХ КОНСТРУКЦИЯХ. например, система Фуллера.

СКЕЛЕТ ОДНОКЛЕТОЧНОГО ОРГАНИЗМА ФЕОДАРИИ ПО ФОРМЕ НАПОМИНАЕТ ИКОСАЭДР

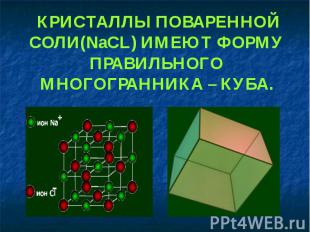
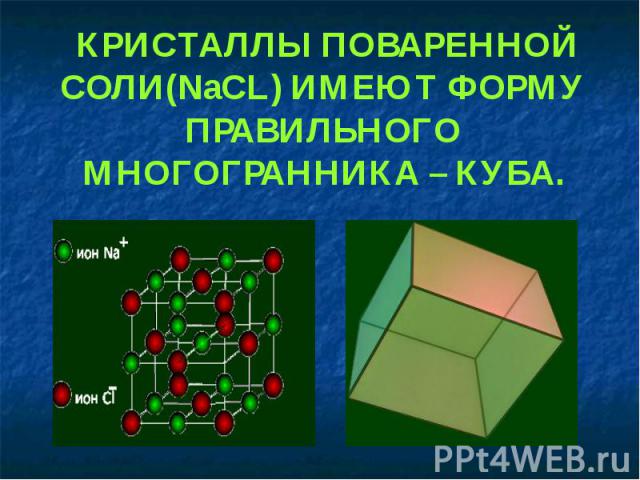
КРИСТАЛЛЫ ПОВАРЕННОЙ СОЛИ(NaCL) ИМЕЮТ ФОРМУ ПРАВИЛЬНОГО МНОГОГРАННИКА – КУБА.

(K[Al(SO4)2] ∙ 12H2O)

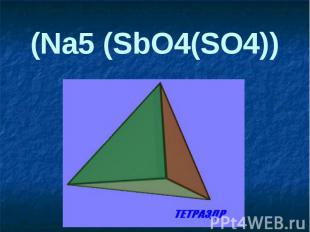
(Na5 (SbO4(SO4))

БЛАГОДАРЯ ПРАВИЛЬНЫМ МНОГОГРАННИКАМ ОТКРЫВАЮТСЯ НЕ ТОЛЬКО СВОЙСТВА ГЕОМЕТРИЧЕСКИХ ФИГУР, НО И ПУТИ ПОЗНАНИЯ ПРИРОДНОЙ ГАРМОНИИ.