Презентация на тему: Вращательные движение твердого тела

Вращательным движением твёрдого тела или системы тел называется такое движение, при котором все точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения, а плоскости окружностей перпендикулярны оси вращения. Вращательным движением твёрдого тела или системы тел называется такое движение, при котором все точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения, а плоскости окружностей перпендикулярны оси вращения. Ось вращения может располагаться внутри тела и за его пределами и в зависимости от выбора системы отсчёта может быть как подвижной, так и неподвижной. Теорема вращения Эйлера утверждает, что любое вращение трёхмерного пространства имеет ось.

Кинематика вращательного движения……………………….…….4 Кинематика вращательного движения……………………….…….4 Динамика вращательного движения……………………………….13 Основное уравнение динамики вращательного движения……14 Динамика произвольного движения………………………………..……….26 Законы сохранения …………………………………………………….....30 Закон сохранения момента импульса…………………………………….31 Кинетическая энергия вращающегося тела…………………………….52 Закон сохранения энергии………………………….………………………….…57 Заключение…………………………………………………………………..…..61 Использованные информационные материалы..…………...66

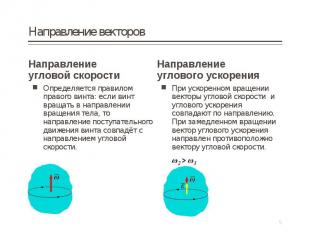
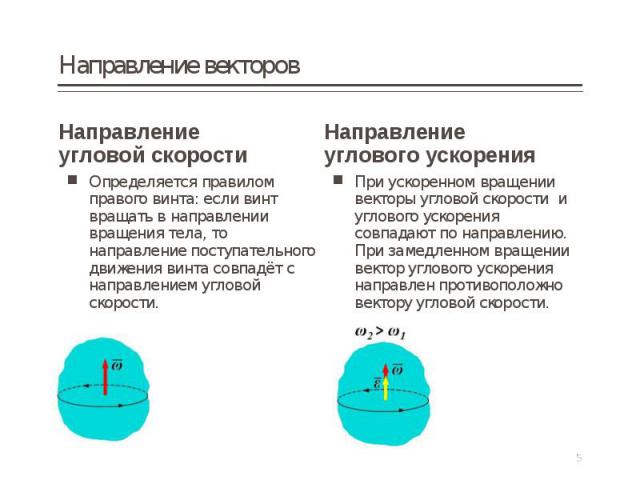
Направление Направление угловой скорости

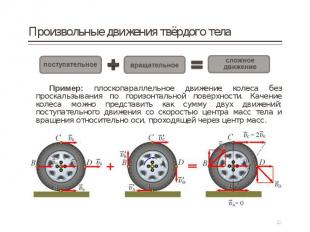
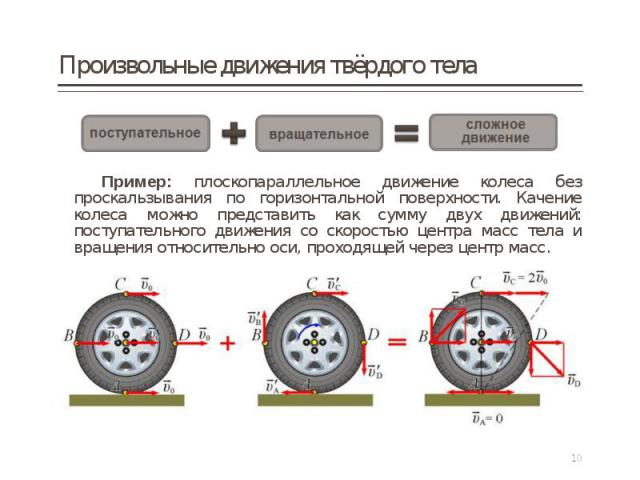
Пример: плоскопараллельное движение колеса без проскальзывания по горизонтальной поверхности. Качение колеса можно представить как сумму двух движений: поступательного движения со скоростью центра масс тела и вращения относительно оси, проходящей через центр масс. Пример: плоскопараллельное движение колеса без проскальзывания по горизонтальной поверхности. Качение колеса можно представить как сумму двух движений: поступательного движения со скоростью центра масс тела и вращения относительно оси, проходящей через центр масс.

Методом последовательной съёмки запечатлена кинематика движения Дворцового моста в Санкт-Петербурге. Выдержка 6 секунд. Какую информацию о движении моста можно извлечь из фотографии? Проанализируйте кинематику его движения. Методом последовательной съёмки запечатлена кинематика движения Дворцового моста в Санкт-Петербурге. Выдержка 6 секунд. Какую информацию о движении моста можно извлечь из фотографии? Проанализируйте кинематику его движения.

Кикоин А.К. Формулы кинематики для вращательного движения. «Квант», 1983, № 11. Кикоин А.К. Формулы кинематики для вращательного движения. «Квант», 1983, № 11. Фистуль М. Кинематика плоскопараллельного движения. «Квант», 1990, № 9 Черноуцан А.И. Когда вокруг всё вертится... «Квант», 1992, № 9. Чивилёв В., Движение по окружности: равномерное и неравномерное. «Квант», 1994, №6. Чивилёв В.И. Кинематика вращательного движения. «Квант», 1986, № 11.

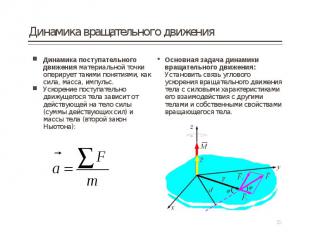
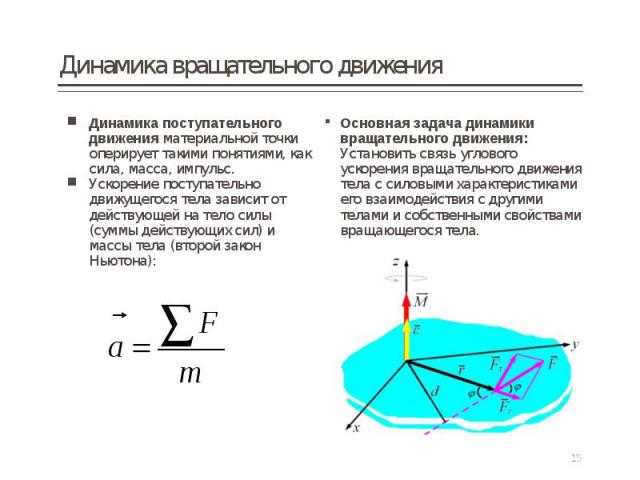
Динамика поступательного движения материальной точки оперирует такими понятиями, как сила, масса, импульс. Динамика поступательного движения материальной точки оперирует такими понятиями, как сила, масса, импульс. Ускорение поступательно движущегося тела зависит от действующей на тело силы (суммы действующих сил) и массы тела (второй закон Ньютона):

Для произвольной точки тела массой m Для произвольной точки тела массой m

Устройство и принцип действия прибора Устройство и принцип действия прибора Исследование зависимости углового ускорения вращения диска от момента действующей силы: от величины действующей силы F при неизменном значении плеча силы относительно данной оси вращения d (d = const); от плеча силы относительно данной оси вращения при постоянной действующей силе (F = const); от суммы моментов всех действующих на тело сил относительно данной оси вращения. Исследование зависимости углового ускорения от свойств вращающегося тела: от массы вращающегося тела при неизменном моменте сил; от распределения массы относительно оси вращения при неизменном моменте сил. Результаты опытов:

Принципиальная разница: масса является инвариантом и не зависит от того, как тело движется. Момент инерции изменяется при изменении положения оси вращения или её направления в пространстве. Принципиальная разница: масса является инвариантом и не зависит от того, как тело движется. Момент инерции изменяется при изменении положения оси вращения или её направления в пространстве.

Виртуальный эксперимент с моделью «Момент инерции» Виртуальный эксперимент с моделью «Момент инерции»

Теорема о переносе осей инерции (Штейнера): момент инерции твёрдого тела относительно произвольной оси I равен сумме момента инерции этого тела I0  относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями: Теорема о переносе осей инерции (Штейнера): момент инерции твёрдого тела относительно произвольной оси I равен сумме момента инерции этого тела I0  относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

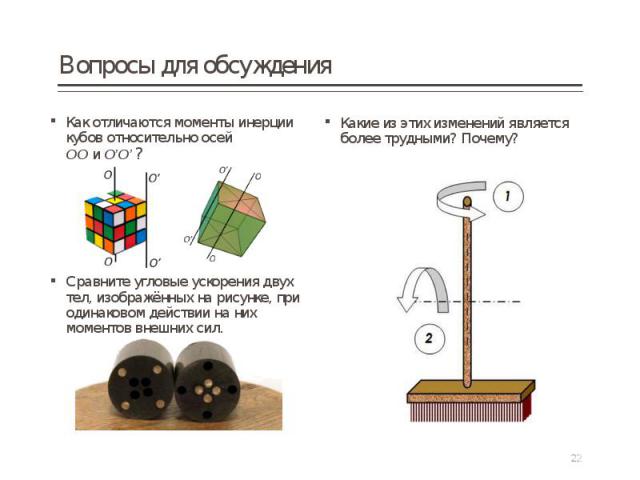
Как отличаются моменты инерции кубов относительно осей ОО и О’О’ ? Как отличаются моменты инерции кубов относительно осей ОО и О’О’ ? Сравните угловые ускорения двух тел, изображённых на рисунке, при одинаковом действии на них моментов внешних сил.

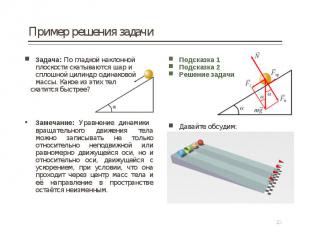
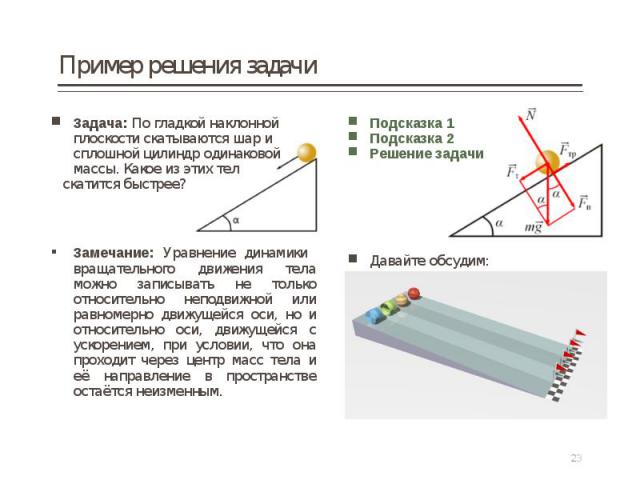
Задача: По гладкой наклонной плоскости скатываются шар и сплошной цилиндр одинаковой массы. Какое из этих тел Задача: По гладкой наклонной плоскости скатываются шар и сплошной цилиндр одинаковой массы. Какое из этих тел скатится быстрее? Замечание: Уравнение динамики вращательного движения тела можно записывать не только относительно неподвижной или равномерно движущейся оси, но и относительно оси, движущейся с ускорением, при условии, что она проходит через центр масс тела и её направление в пространстве остаётся неизменным.

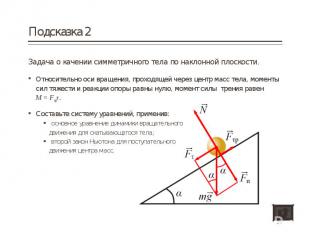
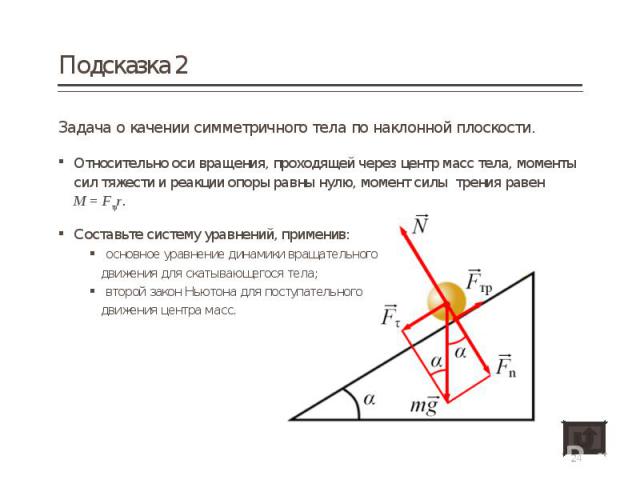
Задача о качении симметричного тела по наклонной плоскости. Задача о качении симметричного тела по наклонной плоскости. Относительно оси вращения, проходящей через центр масс тела, моменты сил тяжести и реакции опоры равны нулю, момент силы трения равен M = Fтрr. Составьте систему уравнений, применив: основное уравнение динамики вращательного движения для скатывающегося тела; второй закон Ньютона для поступательного движения центра масс.

Момент инерции шара и сплошного цилиндра соответственно равны Момент инерции шара и сплошного цилиндра соответственно равны Уравнение вращательного движения: Уравнение второго закона Ньютона для поступательного движения центра масс Ускорение шара и цилиндра при скатывании с наклонной плоскости соответственно равны: aш > aц, следовательно, шар будет скатываться быстрее цилиндра. Обобщая полученный результат на случай скатывания симметричных тел с наклонной плоскости, получим, что быстрее будет скатываться тело, обладающее меньшим моментом инерции.

Произвольное движение твёрдого тела можно разложить на поступательное движение, в котором все точки тела движутся со скоростью центра масс тела, и вращение вокруг центра масс. Произвольное движение твёрдого тела можно разложить на поступательное движение, в котором все точки тела движутся со скоростью центра масс тела, и вращение вокруг центра масс.

Режим последовательной съёмки позволяет проиллюстрировать теорему о движении центра масс системы: при спуске затвора за одну секунду можно запечатлеть несколько изображений. При объединении такой серии спортсмены, выполняющие трюки, и животные в движении превращаются в плотную очередь близнецов. Режим последовательной съёмки позволяет проиллюстрировать теорему о движении центра масс системы: при спуске затвора за одну секунду можно запечатлеть несколько изображений. При объединении такой серии спортсмены, выполняющие трюки, и животные в движении превращаются в плотную очередь близнецов.

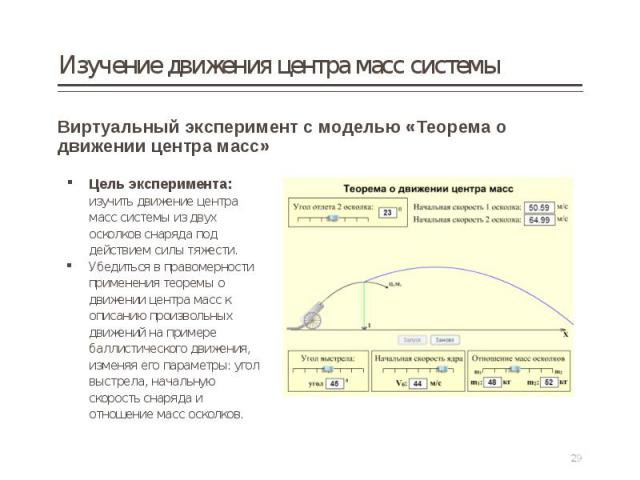
Виртуальный эксперимент с моделью «Теорема о движении центра масс» Виртуальный эксперимент с моделью «Теорема о движении центра масс»

Поступательное движение Поступательное движение

Закон сохранения момента импульса - один из важнейших фундаментальных законов природы - является следствием изотропности пространства (симметрии относительно поворотов в пространстве). Закон сохранения момента импульса - один из важнейших фундаментальных законов природы - является следствием изотропности пространства (симметрии относительно поворотов в пространстве). Закон сохранения момента импульса не является следствием законов Ньютона. Предложенный подход к выводу закона носит частный характер. При сходной алгебраической форме записи законы сохранения импульса и момента импульса в применении к одному телу имеют разный смысл: в отличие от скорости поступательного движения угловая скорость вращения тела может меняться за счёт изменения момента инерции тела I внутренними силами. Закон сохранения момента импульса выполняется для любых физических систем и процессов, не только механических.

Момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на неё, равен нулю. Момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на неё, равен нулю. Следствия из закона сохранения момента импульса в случае изменения скорости вращения одной части системы другая также изменит скорость вращения, но в противоположную сторону таким образом, что момент импульса системы не изменится; если момент инерции замкнутой системы в процессе вращения изменяется, то изменяется и её угловая скорость таким образом, что момент импульса системы останется тем же самым в случае, когда сумма моментов внешних сил относительно некоторой оси равняется нулю, момент импульса системы относительно этой же оси остается постоянным. Экспериментальная проверка. Опыты со скамьёй Жуковского Границы применимости. Закон сохранения момента импульса выполняется в инерциальных системах отсчёта.

Скамья Жуковского состоит станины с опорным шариковым подшипником, в котором вращается круглая горизонтальная платформа.  Скамья Жуковского состоит станины с опорным шариковым подшипником, в котором вращается круглая горизонтальная платформа.  Скамью с человеком приводят во вращение, предложив ему развести руки с гантелями в стороны, а затем резко прижать их к груди.

Закон сохранения момента импульса выполняется, если: Закон сохранения момента импульса выполняется, если: сумма моментов внешних сил равна нулю (силы при этом могут не уравновешиваться); тело движется в центральном силовом поле (при отсутствии других внешних сил; относительно центра поля) Закон сохранения момента импульса применяют: когда характер изменения со временем сил взаимодействия между частями системы сложен или неизвестен; относительно одной и той же оси для всех моментов импульса и сил; как к полностью, так и частично изолированным системам.

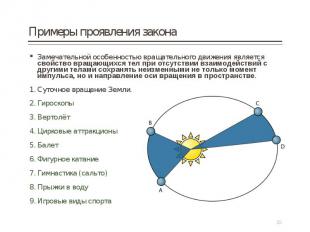
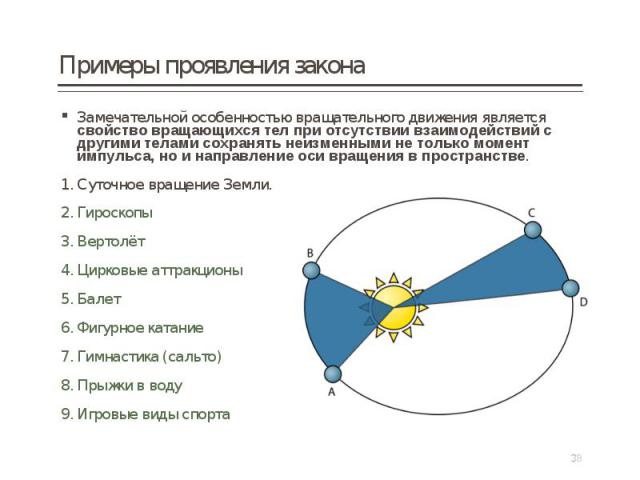
Замечательной особенностью вращательного движения является свойство вращающихся тел при отсутствии взаимодействий с другими телами сохранять неизменными не только момент импульса, но и направление оси вращения в пространстве. Замечательной особенностью вращательного движения является свойство вращающихся тел при отсутствии взаимодействий с другими телами сохранять неизменными не только момент импульса, но и направление оси вращения в пространстве. Суточное вращение Земли. Гироскопы Вертолёт Цирковые аттракционы Балет Фигурное катание Гимнастика (сальто) Прыжки в воду Игровые виды спорта

Неизменным ориентиром для путешественников на поверхности Земли служит Полярная звезда в созвездии Большой Медведицы. Примерно на эту звезду направлена ось вращения Земли, и кажущаяся неподвижность Полярной звезды на протяжении столетий наглядно доказывает, что на протяжении этого времени направление оси вращения Земли в пространстве остается неизменным. Неизменным ориентиром для путешественников на поверхности Земли служит Полярная звезда в созвездии Большой Медведицы. Примерно на эту звезду направлена ось вращения Земли, и кажущаяся неподвижность Полярной звезды на протяжении столетий наглядно доказывает, что на протяжении этого времени направление оси вращения Земли в пространстве остается неизменным.

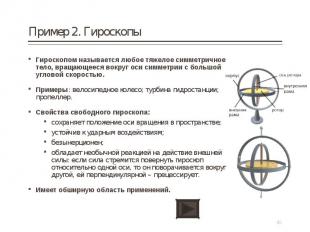
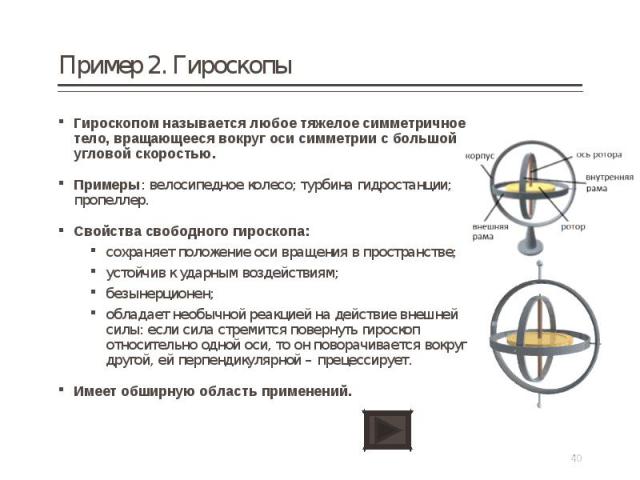
Гироскопом называется любое тяжелое симметричное тело, вращающееся вокруг оси симметрии с большой угловой скоростью. Гироскопом называется любое тяжелое симметричное тело, вращающееся вокруг оси симметрии с большой угловой скоростью. Примеры: велосипедное колесо; турбина гидростанции; пропеллер. Свойства свободного гироскопа: сохраняет положение оси вращения в пространстве; устойчив к ударным воздействиям; безынерционен; обладает необычной реакцией на действие внешней силы: если сила стремится повернуть гироскоп относительно одной оси, то он поворачивается вокруг другой, ей перпендикулярной – прецессирует. Имеет обширную область применений.

Многие особенности поведения вертолёта в воздухе диктуются гироскопическим эффектом. Тело, раскрученное по оси, стремится сохранить неизменным направление этой оси. Многие особенности поведения вертолёта в воздухе диктуются гироскопическим эффектом. Тело, раскрученное по оси, стремится сохранить неизменным направление этой оси. Гироскопическими свойствами обладают валы турбин, велосипедные колеса, и даже элементарные частицы, например, электроны в атоме.

Свойством угловой скорости вращения тела изменяться за счёт действия внутренних сил пользуются спортсмены и артисты балета: когда под действием внутренних сил человек изменяет позу, прижимая руки к туловищу или разводя их в стороны, он изменяет момент импульса своего тела, при этом момент импульса сохраняется как по величине, так и по направлению, поэтому угловая скорость вращения также меняется. Свойством угловой скорости вращения тела изменяться за счёт действия внутренних сил пользуются спортсмены и артисты балета: когда под действием внутренних сил человек изменяет позу, прижимая руки к туловищу или разводя их в стороны, он изменяет момент импульса своего тела, при этом момент импульса сохраняется как по величине, так и по направлению, поэтому угловая скорость вращения также меняется.

Фигурист, совершающий вращение вокруг вертикальной оси, в начале вращения приближает руки к корпусу, тем самым уменьшая момент инерции и увеличивая угловую скорость. В конце вращения происходит обратный процесс: при разведении рук увеличивается момент инерции и уменьшается угловая скорость, что позволяет легко остановить вращение и приступить к выполнению другого элемента. Фигурист, совершающий вращение вокруг вертикальной оси, в начале вращения приближает руки к корпусу, тем самым уменьшая момент инерции и увеличивая угловую скорость. В конце вращения происходит обратный процесс: при разведении рук увеличивается момент инерции и уменьшается угловая скорость, что позволяет легко остановить вращение и приступить к выполнению другого элемента.

Гимнаст, выполняющий сальто, в начальной фазе сгибает колени и прижимает их к груди, уменьшая тем самым момент инерции и увеличивая угловую скорость вращения вокруг горизонтальной оси. В конце прыжка тело выпрямляется, момент инерции возрастает, а угловая скорость уменьшается. Гимнаст, выполняющий сальто, в начальной фазе сгибает колени и прижимает их к груди, уменьшая тем самым момент инерции и увеличивая угловую скорость вращения вокруг горизонтальной оси. В конце прыжка тело выпрямляется, момент инерции возрастает, а угловая скорость уменьшается.

Толчок, испытываемый прыгуном в воду, в момент отрыва от гибкой доски, «закручивает» его, сообщая начальный запас момента импульса относительно центра масс. Толчок, испытываемый прыгуном в воду, в момент отрыва от гибкой доски, «закручивает» его, сообщая начальный запас момента импульса относительно центра масс. Перед входом в воду, совершив один или несколько оборотов с большой угловой скоростью, спортсмен вытягивает руки, увеличивая тем самым свой момент инерции и, следовательно, снижая свою угловую скорость.

Вращение устойчиво относительно главных осей инерции, совпадающих с осями симметрии тел. Вращение устойчиво относительно главных осей инерции, совпадающих с осями симметрии тел. Если в начальный момент угловая скорость немного отклоняется по направлению от оси, которой соответствует промежуточное значение момента инерции, то в дальнейшем угол отклонения стремительно нарастает, и вместо простого равномерного вращения вокруг неизменного направления тело начинает совершать беспорядочное на вид кувыркание.

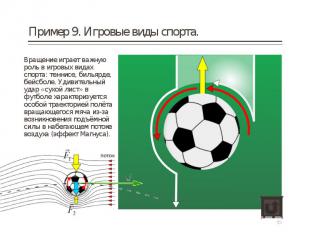
Вращение играет важную роль в игровых видах спорта: теннисе, бильярде, бейсболе. Удивительный удар «сухой лист» в футболе характеризуется особой траекторией полёта вращающегося мяча из-за возникновения подъёмной силы в набегающем потоке воздуха (эффект Магнуса). Вращение играет важную роль в игровых видах спорта: теннисе, бильярде, бейсболе. Удивительный удар «сухой лист» в футболе характеризуется особой траекторией полёта вращающегося мяча из-за возникновения подъёмной силы в набегающем потоке воздуха (эффект Магнуса).

Космический телескоп Хаббл свободно плавает в пространстве. Как можно изменить его ориентацию так, чтобы нацелить на важные для астрономов объекты? Космический телескоп Хаббл свободно плавает в пространстве. Как можно изменить его ориентацию так, чтобы нацелить на важные для астрономов объекты?

Почему кошка при падении всегда приземляется на лапы? Почему кошка при падении всегда приземляется на лапы? Почему трудно удерживать равновесие на неподвижном двухколёсном велосипеде и совсем нетрудно, когда велосипед движется? Как поведёт себя кабина вертолёта, находящегося в полёте, если по каким-либо причинам хвостовой винт перестанет работать?

Кинетическая энергия вращающегося тела равна сумме кинетических энергий отдельных его частей: Кинетическая энергия вращающегося тела равна сумме кинетических энергий отдельных его частей: Поскольку угловые скорости всех точек вращающегося тела одинаковы, то, используя связь линейной и угловой скоростей, получим: Величина, стоящая в скобках, представляет собой момент инерции тела относительно оси вращения: Формула кинетической энергии вращающегося тела:

При плоском движении кинетическая энергия твёрдого тела равна сумме кинетической энергии вращения вокруг оси, проходящей через центр масс, и кинетической энергии поступательного движения центра масс: При плоском движении кинетическая энергия твёрдого тела равна сумме кинетической энергии вращения вокруг оси, проходящей через центр масс, и кинетической энергии поступательного движения центра масс: Это же тело может иметь еще и потенциальную энергию ЕP, если оно взаимодействует с другими телами. Тогда полная энергия равна:

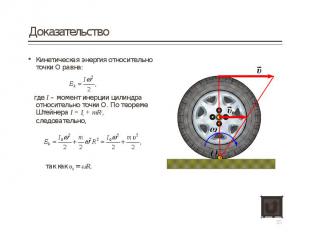
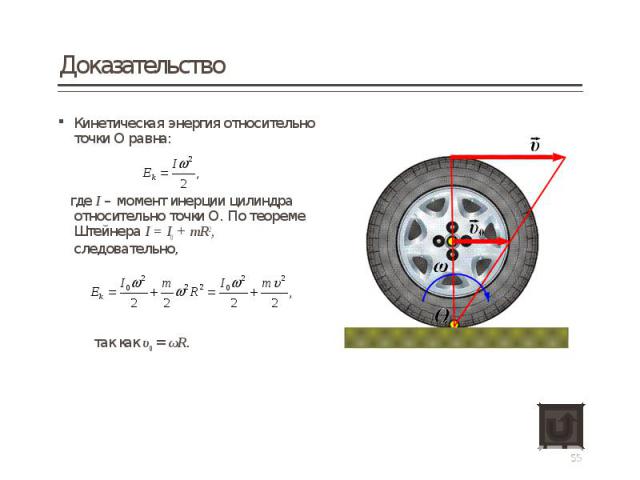
Кинетическая энергия относительно точки О равна: Кинетическая энергия относительно точки О равна: где I – момент инерции цилиндра относительно точки О. По теореме Штейнера I = I0 + mR2, следовательно, так как υ0 = ωR.

Кинетическая энергия любой системы материальных точек равна сумме кинетической энергии всей массы системы, мысленно сосредоточенной в ее центре масс и движущейся вместе с ним, и кинетической энергии всех материальных точек той же системы в их относительном движении по отношению к поступательно движущейся системе координат с началом в центре масс. Кинетическая энергия любой системы материальных точек равна сумме кинетической энергии всей массы системы, мысленно сосредоточенной в ее центре масс и движущейся вместе с ним, и кинетической энергии всех материальных точек той же системы в их относительном движении по отношению к поступательно движущейся системе координат с началом в центре масс.

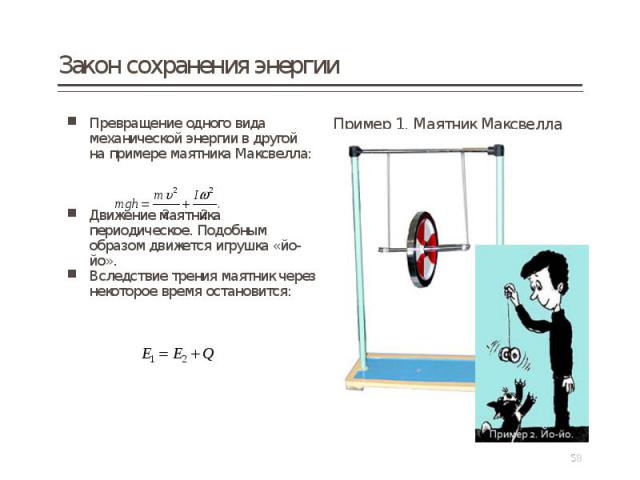
Превращение одного вида механической энергии в другой на примере маятника Максвелла: Превращение одного вида механической энергии в другой на примере маятника Максвелла: Движение маятника периодическое. Подобным образом движется игрушка «йо-йо». Вследствие трения маятник через некоторое время остановится:

Толкание ядра, метание молота, диска и других спортивных снарядов требуют предварительного разгона для увеличения дальности полёта. Толкание ядра, метание молота, диска и других спортивных снарядов требуют предварительного разгона для увеличения дальности полёта. Увеличение скорости снаряда при отрыве от рук метателя (вылете), достигается за счёт дополнительного вращения перед броском.

Зависимость кинетической энергии вращения от момента инерции тел используют в инерционных аккумуляторах. Зависимость кинетической энергии вращения от момента инерции тел используют в инерционных аккумуляторах. Работа, совершаемая за счёт кинетической энергии вращения, равна: Примеры: гончарные круги, массивные колёса водяных мельниц, маховики в двигателях внутреннего сгорания. Маховики, применяемые в прокатных станах, имеют диаметр свыше трёх метров и массу более сорока тонн.

Задачи для самостоятельного Задачи для самостоятельного решения Шар скатывается с наклонной плоскости высотой h = 90 см. Какую линейную скорость будет иметь центр шара в тот момент, когда шар скатится с наклонной плоскости? Решите задачу динамическим и энергетическим способами. Однородный шар массы m и радиуса R скатывается без скольжения по наклонной плоскости, составляющей угол α с горизонтом. Найдите: а) значения коэффициента трения, при которых скольжения не будет; б) кинетическую энергию шара через t секунд после начала движения.

«Так уж повелось издавна, что в конденсаторе, этом хранителе зарядов, существует электрическое поле, а в катушке с током - магнитное. Но повесить конденсатор в магнитном поле - такое могло прийти в голову только очень Любопытному ребенку. И не зря - он узнал нечто новое… Оказывается, - сказал себе Любопытный ребенок, - электромагнитное поле обладает атрибутами механики: плотностью импульса и момента импульса!» (Стасенко А.Л. Зачем быть конденсатору в магнитном поле? Квант, 1998, № 5). «Так уж повелось издавна, что в конденсаторе, этом хранителе зарядов, существует электрическое поле, а в катушке с током - магнитное. Но повесить конденсатор в магнитном поле - такое могло прийти в голову только очень Любопытному ребенку. И не зря - он узнал нечто новое… Оказывается, - сказал себе Любопытный ребенок, - электромагнитное поле обладает атрибутами механики: плотностью импульса и момента импульса!» (Стасенко А.Л. Зачем быть конденсатору в магнитном поле? Квант, 1998, № 5). «А что между ними — реками, тайфунами, молекулами — общего?...» (Стасенко А.Л. Вращение: реки, тайфуны, молекулы. Квант, 1997, № 5).

Читайте книги: Орир Д. Популярная физика. М.: Мир, 1964, или Купер Л. Физика для всех. М.: Мир, 1973. Т. 1. Из них вы узнаете много интересного о движении планет, колёс, волчков, вращении гимнаста на перекладине и... почему кошка всегда падает на лапы. Читайте книги: Орир Д. Популярная физика. М.: Мир, 1964, или Купер Л. Физика для всех. М.: Мир, 1973. Т. 1. Из них вы узнаете много интересного о движении планет, колёс, волчков, вращении гимнаста на перекладине и... почему кошка всегда падает на лапы. Читайте в «Кванте»: Воробьев И. Необычное путешествие. (№2, 1974) Давыдов В. Как индейцы бросают томагавк? (№ 11, 1989)   Джоунс Д., Почему устойчив велосипед (№12, 1970) Кикоин А. Вращательное движение тел  (№1, 1971) Кривошлыков С. Механика вращающегося волчка.  (№ 10, 1971  год) Ланге В. Почему кувыркается книга (N3,2000) Томсон Дж. Дж. О динамике мяча для игры в гольф. (№8, 1990) Используйте образовательные ресурсы сети Интернет: http://physics.nad.ru/Physics/Cyrillic/mech.htm http://howitworks.iknowit.ru/paper1113.html http://class-fizika.narod.ru/9_posmotri.htm и др.

Изучите закономерности вращательного движения с помощью моделирующей программы (Java-апплета) Изучите закономерности вращательного движения с помощью моделирующей программы (Java-апплета) СВОБОДНОЕ ВРАЩЕНИЕ СИММЕТРИЧНОГО ВОЛЧКА СВОБОДНОЕ ВРАЩЕНИЕ ОДНОРОДНОГО ЦИЛИНДРА (СИММЕТРИЧНОГО ВОЛЧКА) ВЫНУЖДЕННАЯ ПРЕЦЕССИЯ ГИРОСКОПА Определите собственный момент инерции методом физического маятника, используя образовательные ресурсы сети Интернет. Выполните экспериментальное исследование «Определение положения центра масс и моментов инерции тела человека относительно анатомических осей». Будьте наблюдательны!

Учебник для 10 класса с углублённым изучением физики под редакцией А. А. Пинского, О. Ф. Кабардина. М. : «Просвещение», 2005. Учебник для 10 класса с углублённым изучением физики под редакцией А. А. Пинского, О. Ф. Кабардина. М. : «Просвещение», 2005. Факультативный курс физики. О. Ф. Кабардин, В. А. Орлов, А. В. Пономарева. М. : «Просвещение», 1977 г. Ремизов А. Н. Курс физики: Учеб. для вузов / А. Н. Ремизов, А. Я. Потапенко. М.: Дрофа, 2004. Трофимова Т. И. Курс физики: Учеб. пособие для вузов. М.: Высшая школа, 1990. http://ru.wikipedia.org/wiki/ http://elementy.ru/trefil/21152 http://www.physics.ru/courses/op25part1/content/chapter1/section/paragraph23/theory.html Physclips . Мультимедийное введение в физику. http://www.animations.physics.unsw.edu.au/jw/rotation.htm и др. В оформлении в учебных целях использованы иллюстративные материалы сети Интернет.