Презентация на тему: Сфера и шар: теоремы, доказательства, история изучения

Сфера и шар. МОУ СОШ №256 г.Фокино.

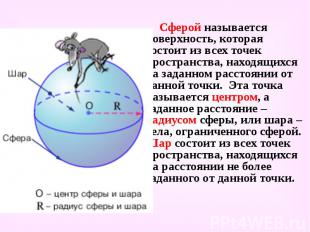
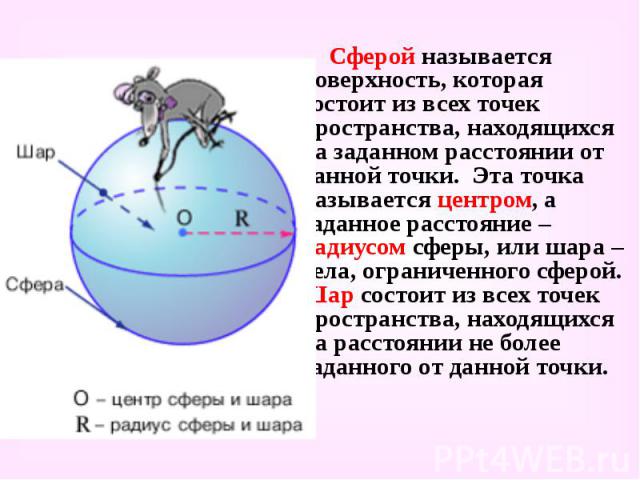
Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром, а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки. Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром, а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.

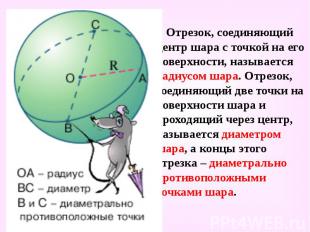
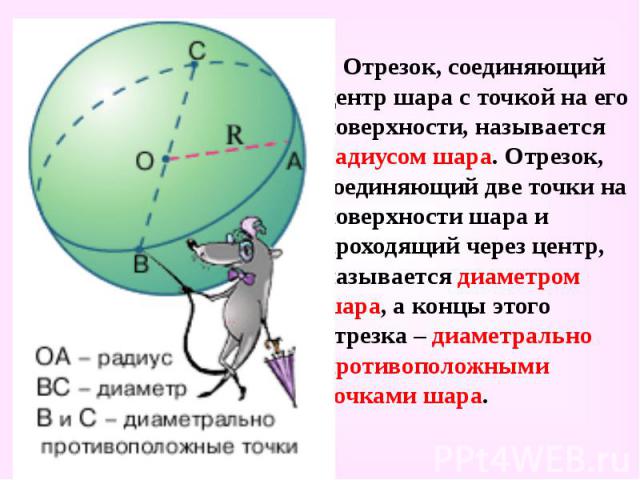
Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом шара. Отрезок, соединяющий две точки на поверхности шара и проходящий через центр, называется диаметром шара, а концы этого отрезка – диаметрально противоположными точками шара. Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом шара. Отрезок, соединяющий две точки на поверхности шара и проходящий через центр, называется диаметром шара, а концы этого отрезка – диаметрально противоположными точками шара.

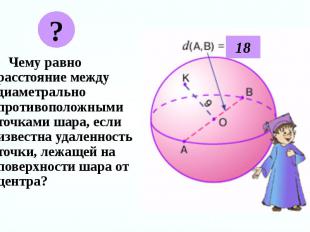
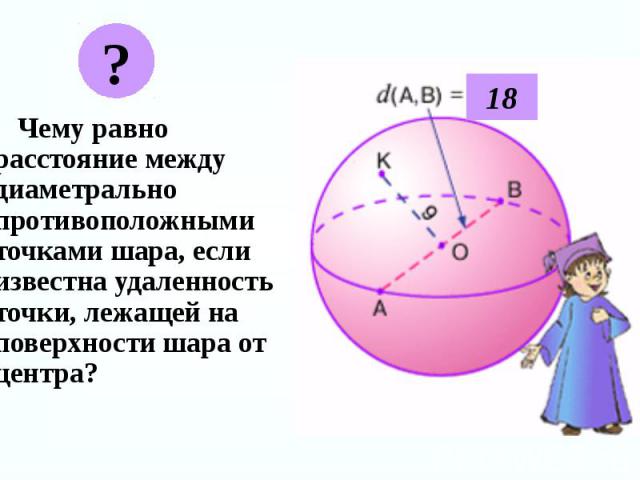
Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность точки, лежащей на поверхности шара от центра? Чему равно расстояние между диаметрально противоположными точками шара, если известна удаленность точки, лежащей на поверхности шара от центра?

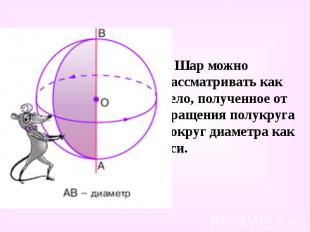
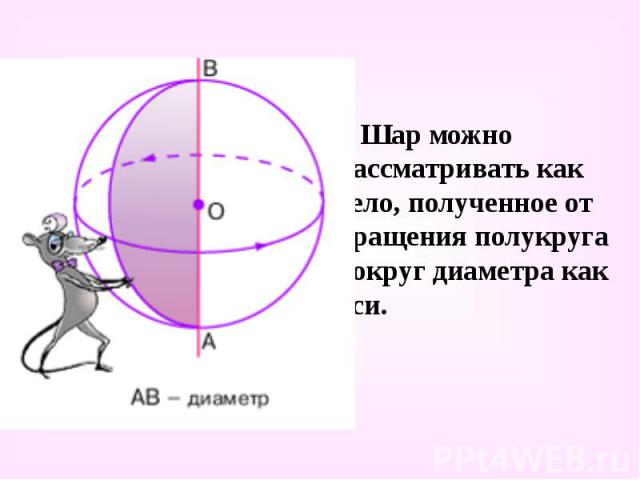
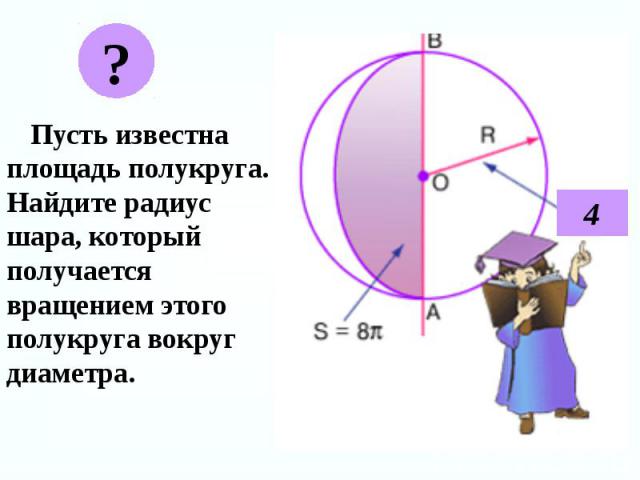
Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси. Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.

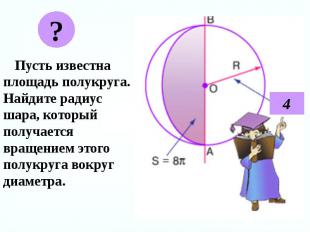
Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра. Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра.

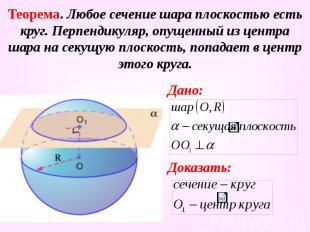
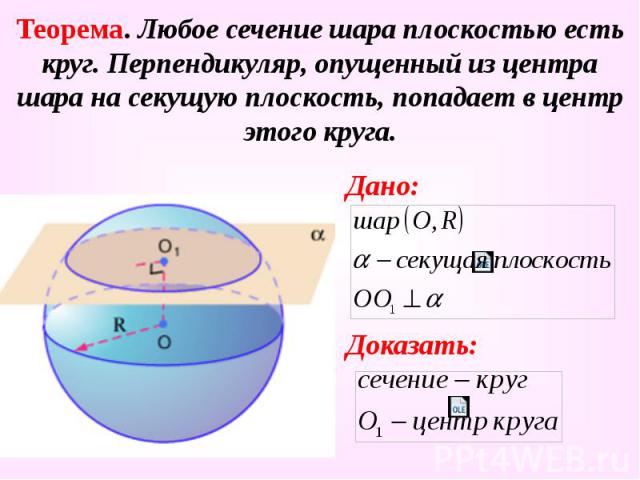
Теорема. Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает в центр этого круга. Дано: Доказать:

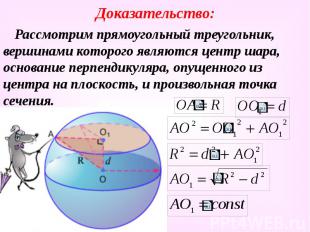
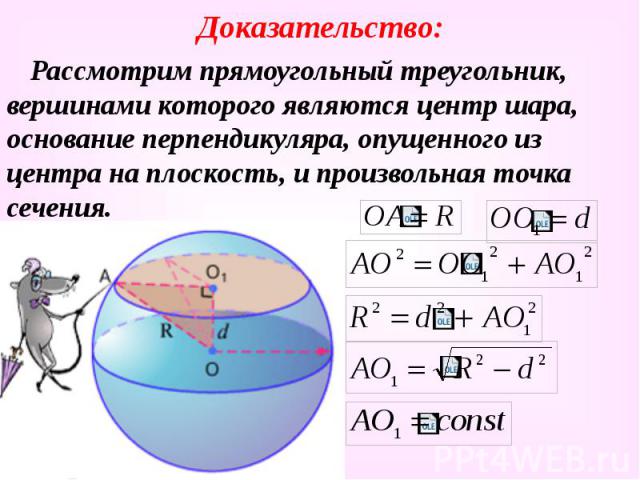
Доказательство: Рассмотрим прямоугольный треугольник, вершинами которого являются центр шара, основание перпендикуляра, опущенного из центра на плоскость, и произвольная точка сечения.

Следствие. Если известны радиус шара и расстояние от центра шара до плоскости сечения, то радиус сечения вычисляется по теореме Пифагора.

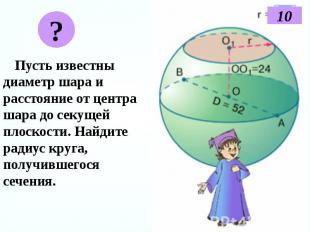
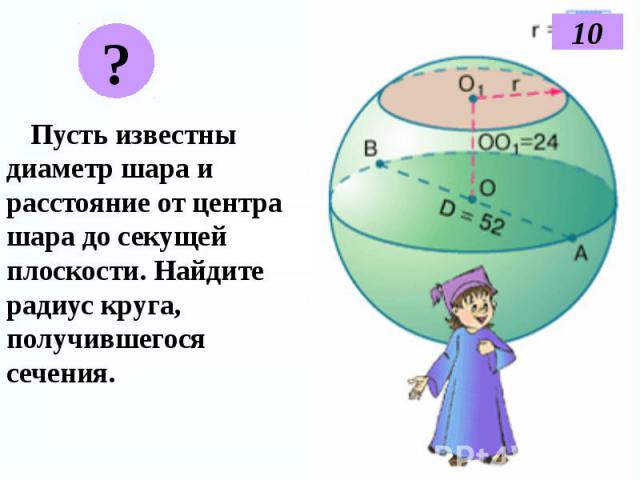
Пусть известны диаметр шара и расстояние от центра шара до секущей плоскости. Найдите радиус круга, получившегося сечения. Пусть известны диаметр шара и расстояние от центра шара до секущей плоскости. Найдите радиус круга, получившегося сечения.

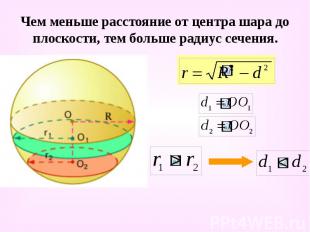
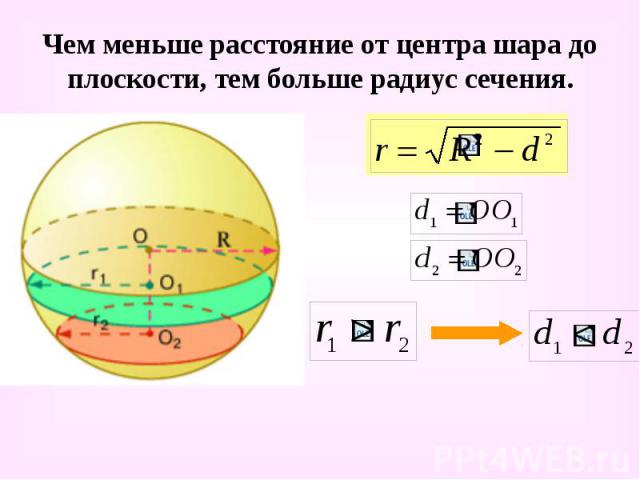
Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения.

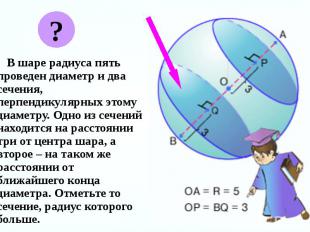
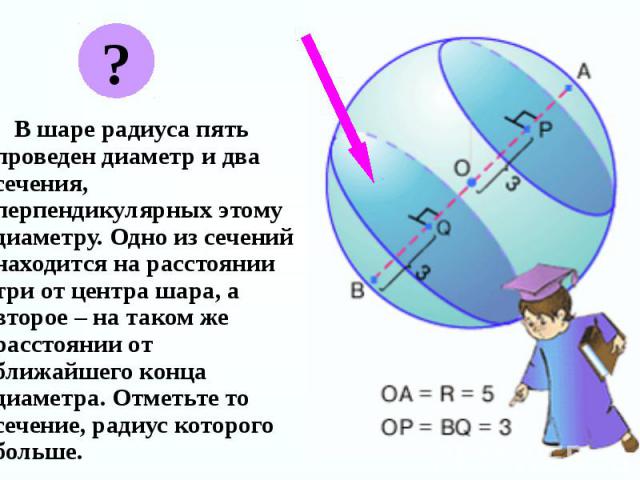
В шаре радиуса пять проведен диаметр и два сечения, перпендикулярных этому диаметру. Одно из сечений находится на расстоянии три от центра шара, а второе – на таком же расстоянии от ближайшего конца диаметра. Отметьте то сечение, радиус которого больше. В шаре радиуса пять проведен диаметр и два сечения, перпендикулярных этому диаметру. Одно из сечений находится на расстоянии три от центра шара, а второе – на таком же расстоянии от ближайшего конца диаметра. Отметьте то сечение, радиус которого больше.

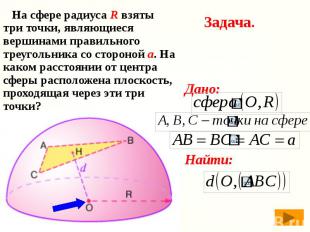
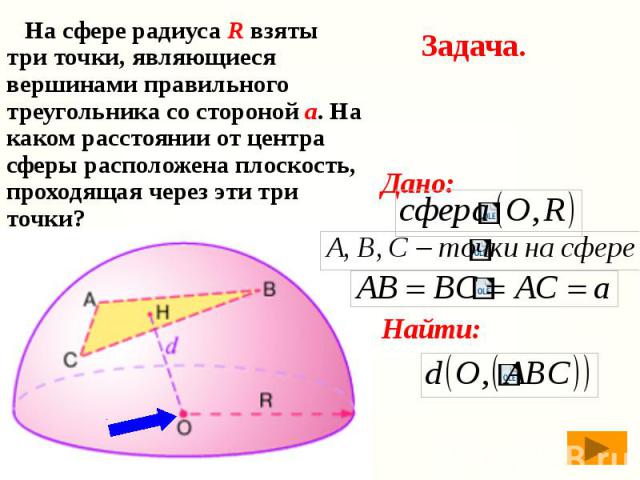
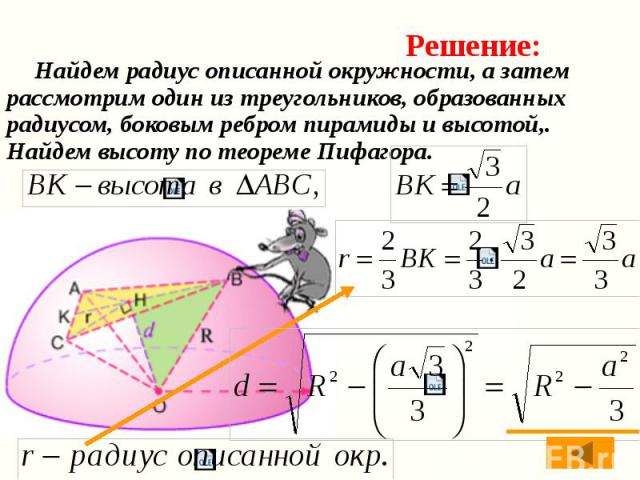
Задача. На сфере радиуса R взяты три точки, являющиеся вершинами правильного треугольника со стороной а. На каком расстоянии от центра сферы расположена плоскость, проходящая через эти три точки?

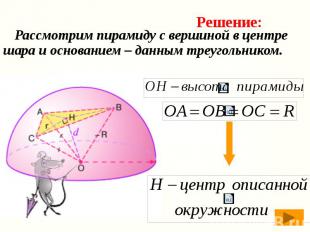
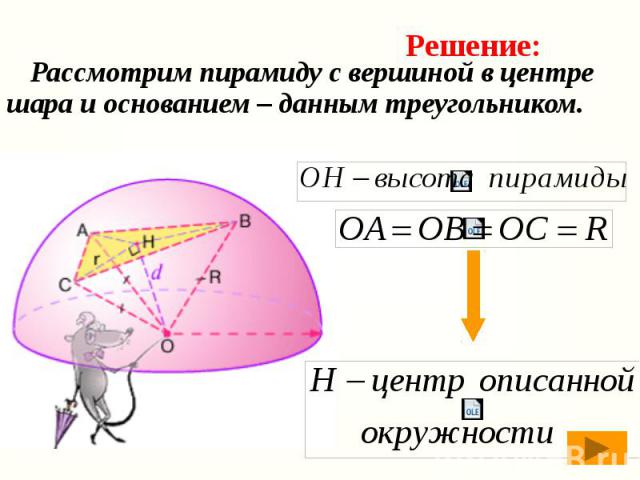
Рассмотрим пирамиду с вершиной в центре шара и основанием – данным треугольником. Рассмотрим пирамиду с вершиной в центре шара и основанием – данным треугольником.

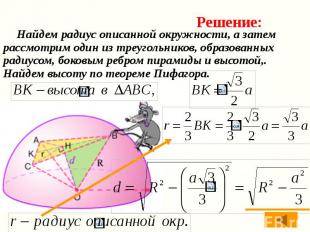
Найдем радиус описанной окружности, а затем рассмотрим один из треугольников, образованных радиусом, боковым ребром пирамиды и высотой,. Найдем высоту по теореме Пифагора. Найдем радиус описанной окружности, а затем рассмотрим один из треугольников, образованных радиусом, боковым ребром пирамиды и высотой,. Найдем высоту по теореме Пифагора.

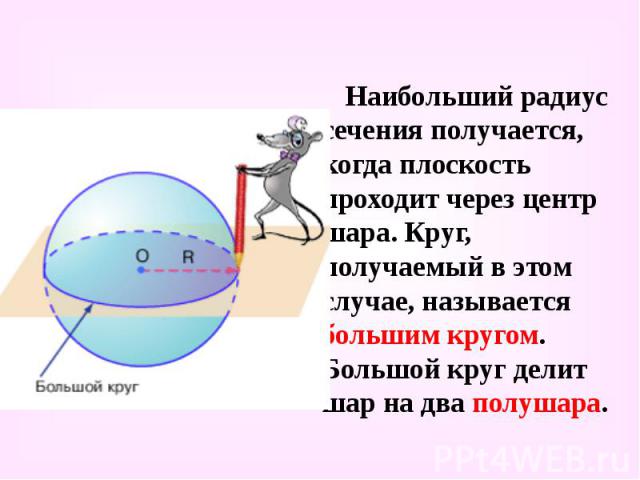
Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг, получаемый в этом случае, называется большим кругом. Большой круг делит шар на два полушара. Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг, получаемый в этом случае, называется большим кругом. Большой круг делит шар на два полушара.

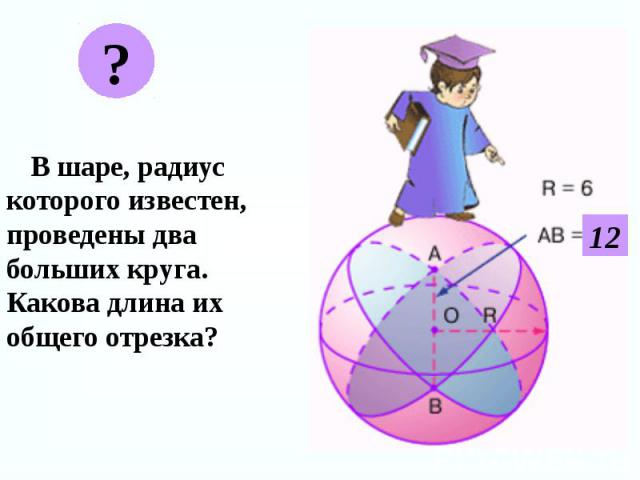
В шаре, радиус которого известен, проведены два больших круга. Какова длина их общего отрезка? В шаре, радиус которого известен, проведены два больших круга. Какова длина их общего отрезка?

Плоскость и прямая, касательные к сфере. Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью. Касательная плоскость перпендикулярна радиусу, проведенному в точку касания.

Пусть шар, радиус которого известен, лежит на горизонтальной плоскости. В этой плоскости через точку касания и точку В проведен отрезок, длина которого известна. Чему равно расстояние от центра шара до противоположного конца отрезка? Пусть шар, радиус которого известен, лежит на горизонтальной плоскости. В этой плоскости через точку касания и точку В проведен отрезок, длина которого известна. Чему равно расстояние от центра шара до противоположного конца отрезка?

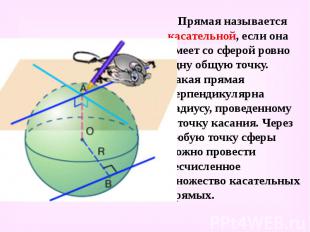
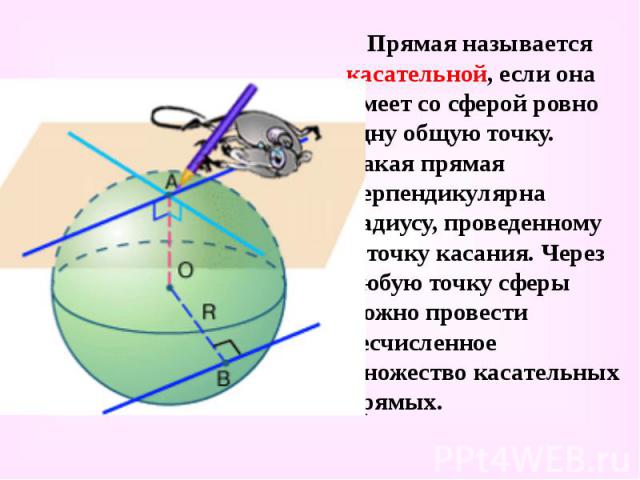
Прямая называется касательной, если она имеет со сферой ровно одну общую точку. Такая прямая перпендикулярна радиусу, проведенному в точку касания. Через любую точку сферы можно провести бесчисленное множество касательных прямых. Прямая называется касательной, если она имеет со сферой ровно одну общую точку. Такая прямая перпендикулярна радиусу, проведенному в точку касания. Через любую точку сферы можно провести бесчисленное множество касательных прямых.

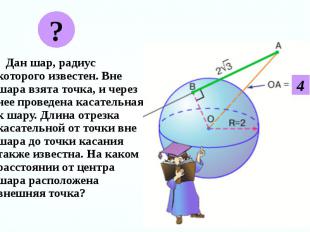
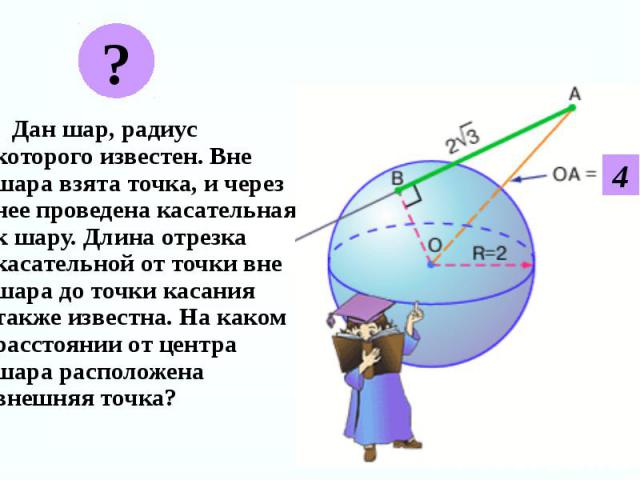
Дан шар, радиус которого известен. Вне шара взята точка, и через нее проведена касательная к шару. Длина отрезка касательной от точки вне шара до точки касания также известна. На каком расстоянии от центра шара расположена внешняя точка? Дан шар, радиус которого известен. Вне шара взята точка, и через нее проведена касательная к шару. Длина отрезка касательной от точки вне шара до точки касания также известна. На каком расстоянии от центра шара расположена внешняя точка?

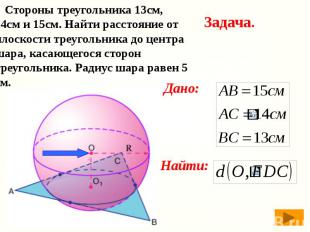
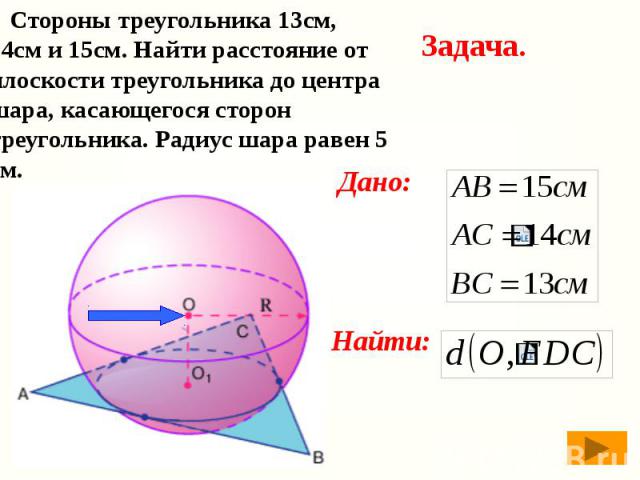
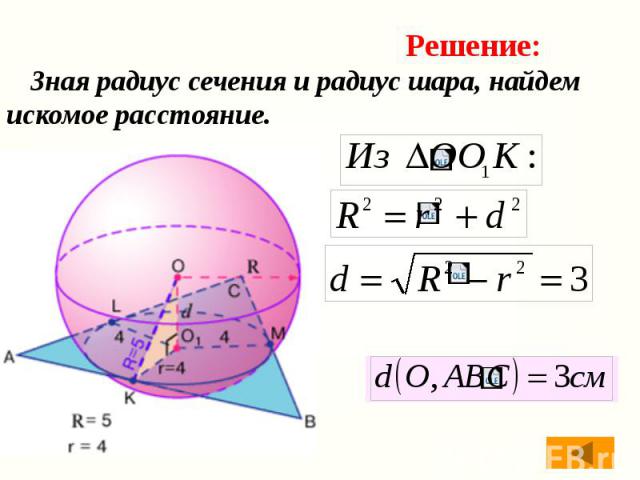
Стороны треугольника 13см, 14см и 15см. Найти расстояние от плоскости треугольника до центра шара, касающегося сторон треугольника. Радиус шара равен 5 см. Стороны треугольника 13см, 14см и 15см. Найти расстояние от плоскости треугольника до центра шара, касающегося сторон треугольника. Радиус шара равен 5 см.

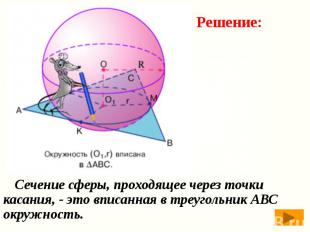
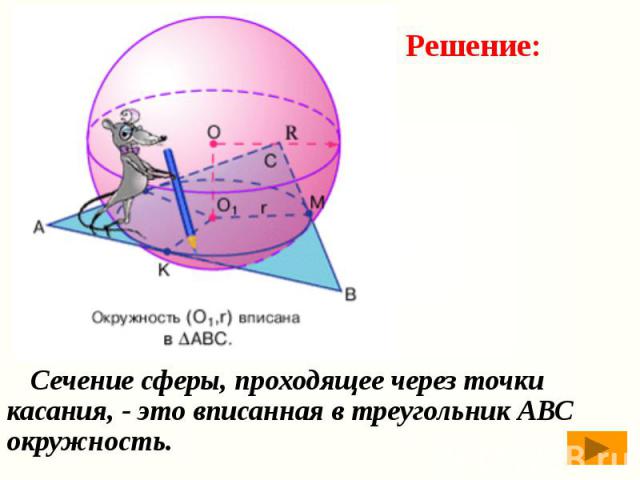
Сечение сферы, проходящее через точки касания, - это вписанная в треугольник АВС окружность. Сечение сферы, проходящее через точки касания, - это вписанная в треугольник АВС окружность.

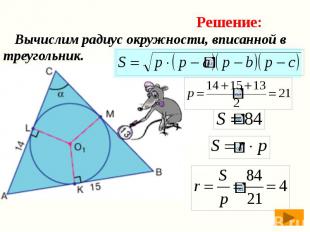
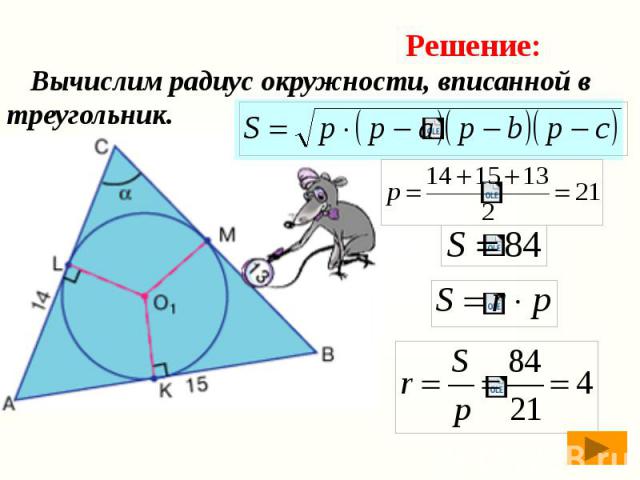
Вычислим радиус окружности, вписанной в треугольник. Вычислим радиус окружности, вписанной в треугольник.

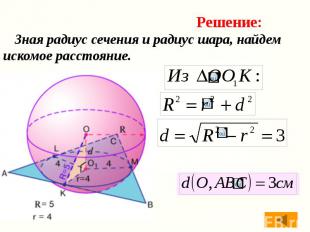
Зная радиус сечения и радиус шара, найдем искомое расстояние. Зная радиус сечения и радиус шара, найдем искомое расстояние.

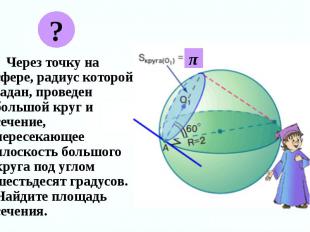
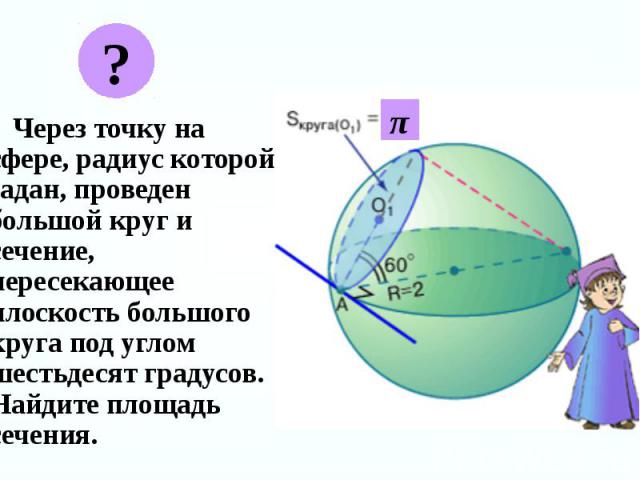
Через точку на сфере, радиус которой задан, проведен большой круг и сечение, пересекающее плоскость большого круга под углом шестьдесят градусов. Найдите площадь сечения. Через точку на сфере, радиус которой задан, проведен большой круг и сечение, пересекающее плоскость большого круга под углом шестьдесят градусов. Найдите площадь сечения.

Взаимное расположение двух шаров. Если два шара или сферы имеют только одну общую точку, то говорят, что они касаются. Их общая касательная плоскость перпендикулярна линии центров (прямой, соединяющей центры обоих шаров).

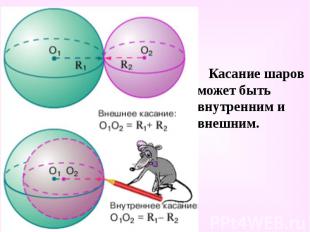
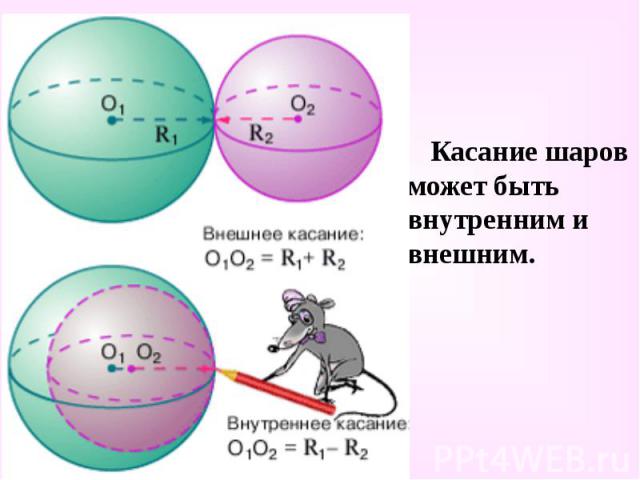
Касание шаров может быть внутренним и внешним. Касание шаров может быть внутренним и внешним.

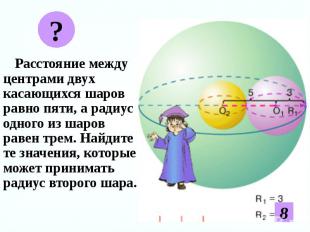
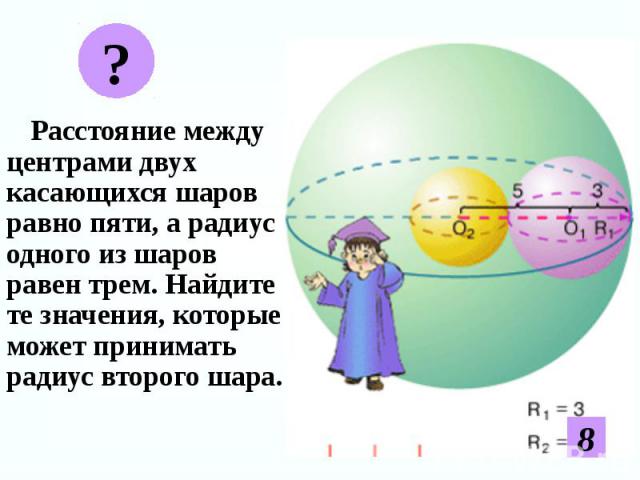
Расстояние между центрами двух касающихся шаров равно пяти, а радиус одного из шаров равен трем. Найдите те значения, которые может принимать радиус второго шара. Расстояние между центрами двух касающихся шаров равно пяти, а радиус одного из шаров равен трем. Найдите те значения, которые может принимать радиус второго шара.

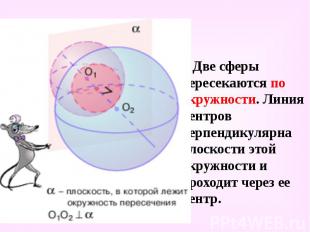
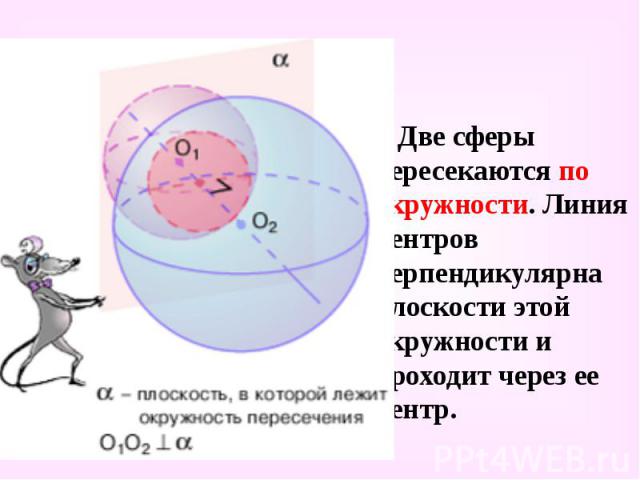
Две сферы пересекаются по окружности. Линия центров перпендикулярна плоскости этой окружности и проходит через ее центр. Две сферы пересекаются по окружности. Линия центров перпендикулярна плоскости этой окружности и проходит через ее центр.

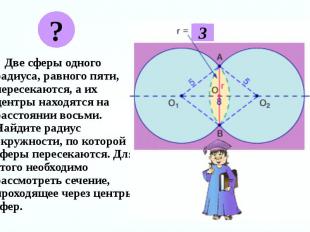
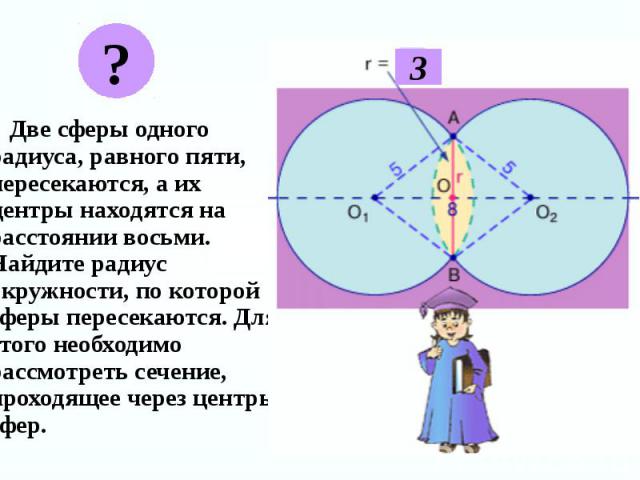
Две сферы одного радиуса, равного пяти, пересекаются, а их центры находятся на расстоянии восьми. Найдите радиус окружности, по которой сферы пересекаются. Для этого необходимо рассмотреть сечение, проходящее через центры сфер. Две сферы одного радиуса, равного пяти, пересекаются, а их центры находятся на расстоянии восьми. Найдите радиус окружности, по которой сферы пересекаются. Для этого необходимо рассмотреть сечение, проходящее через центры сфер.

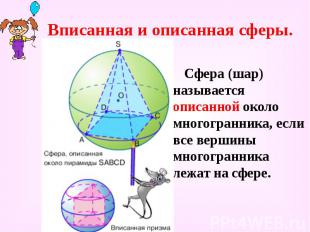
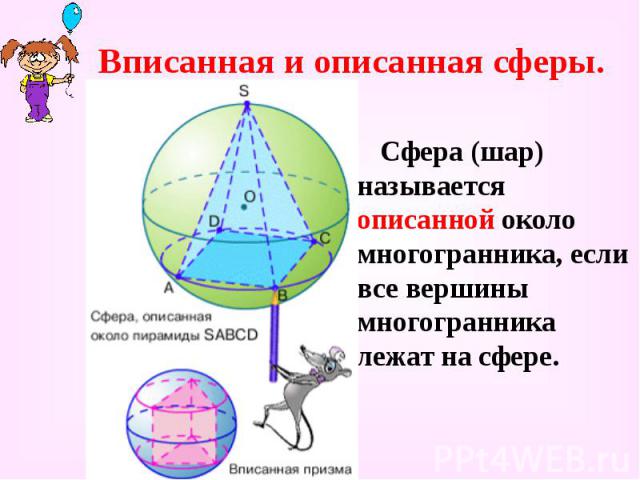
Вписанная и описанная сферы. Сфера (шар) называется описанной около многогранника, если все вершины многогранника лежат на сфере.

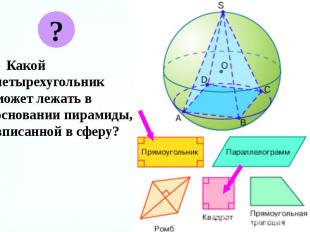
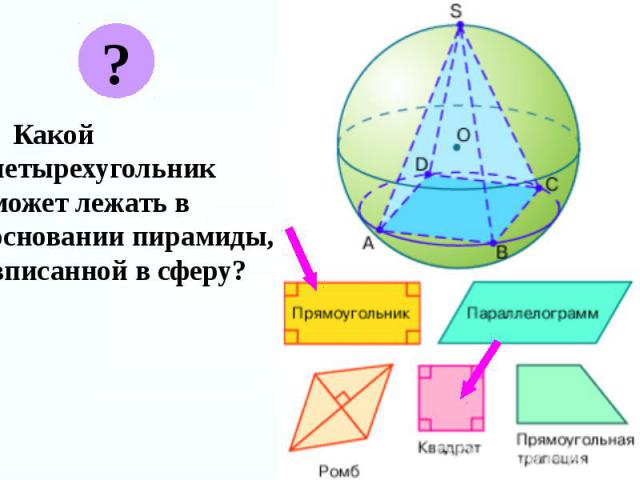
Какой четырехугольник может лежать в основании пирамиды, вписанной в сферу? Какой четырехугольник может лежать в основании пирамиды, вписанной в сферу?

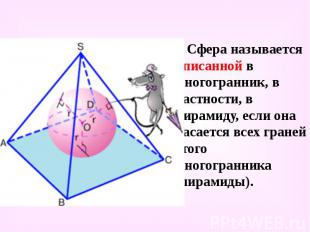
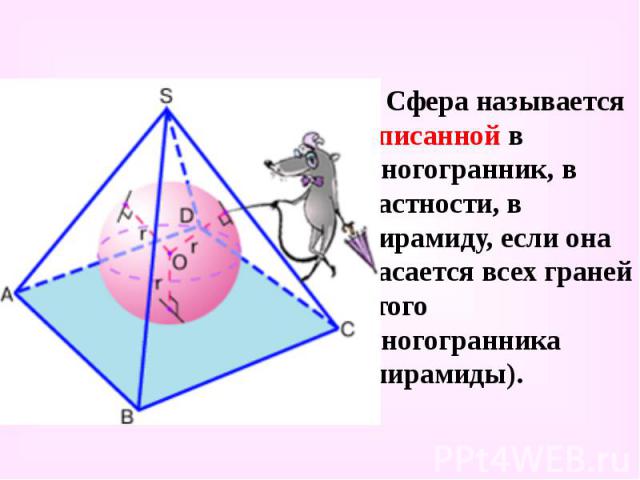
Сфера называется вписанной в многогранник, в частности, в пирамиду, если она касается всех граней этого многогранника (пирамиды). Сфера называется вписанной в многогранник, в частности, в пирамиду, если она касается всех граней этого многогранника (пирамиды).

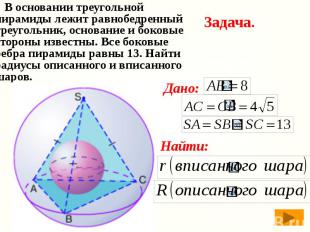
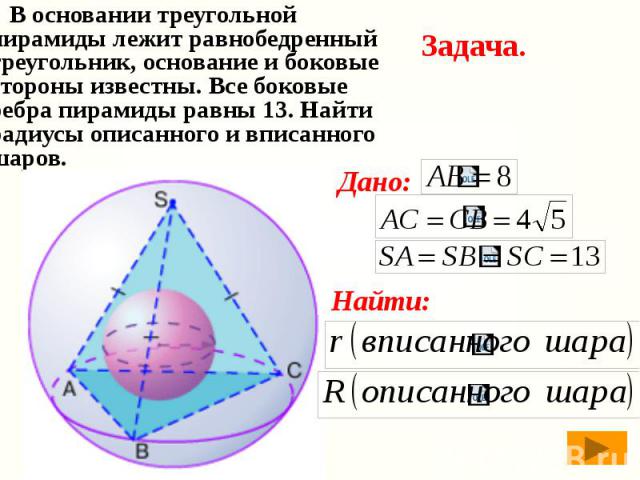
В основании треугольной пирамиды лежит равнобедренный треугольник, основание и боковые стороны известны. Все боковые ребра пирамиды равны 13. Найти радиусы описанного и вписанного шаров. В основании треугольной пирамиды лежит равнобедренный треугольник, основание и боковые стороны известны. Все боковые ребра пирамиды равны 13. Найти радиусы описанного и вписанного шаров.

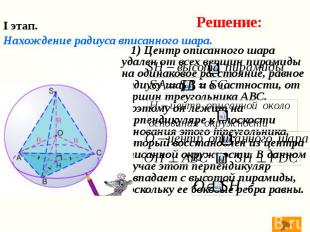
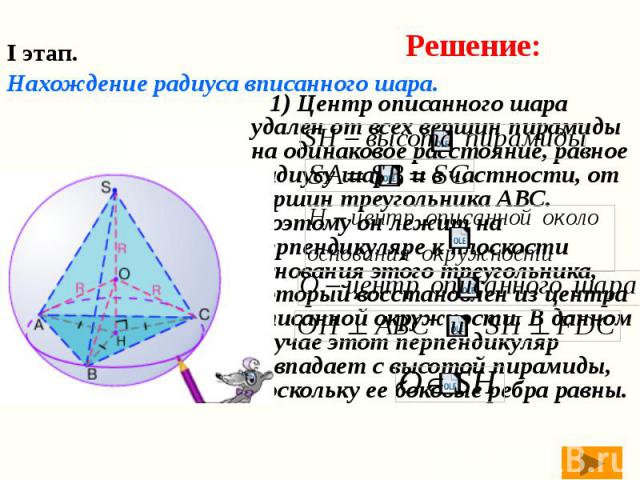
I этап. Нахождение радиуса вписанного шара. 1) Центр описанного шара удален от всех вершин пирамиды на одинаковое расстояние, равное радиусу шара, и в частности, от вершин треугольника АВС. Поэтому он лежит на перпендикуляре к плоскости основания этого треугольника, который восстановлен из центра описанной окружности. В данном случае этот перпендикуляр совпадает с высотой пирамиды, поскольку ее боковые ребра равны.

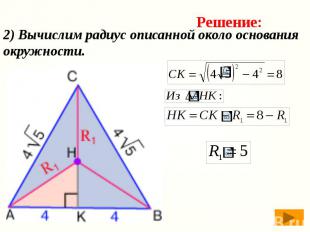
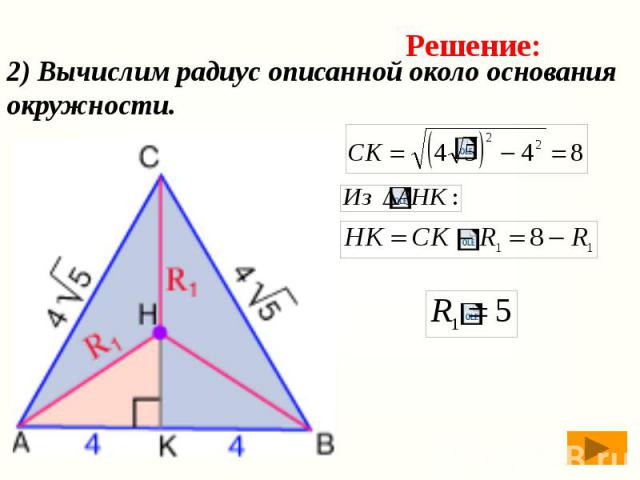
2) Вычислим радиус описанной около основания окружности.

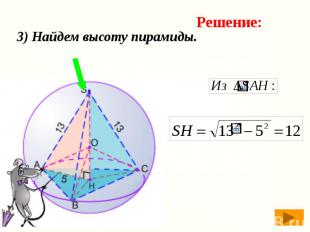
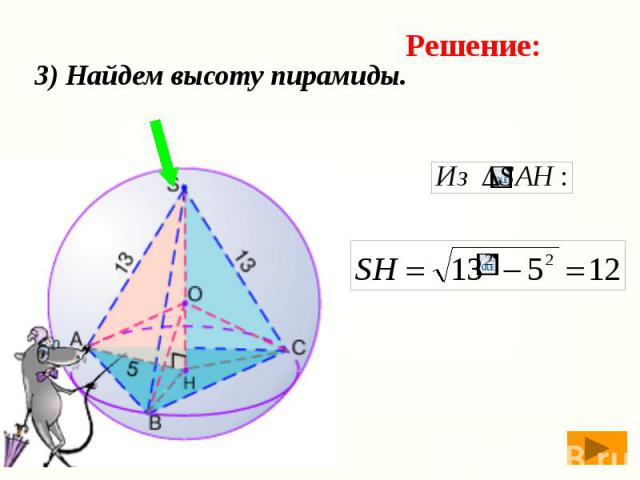
3) Найдем высоту пирамиды.

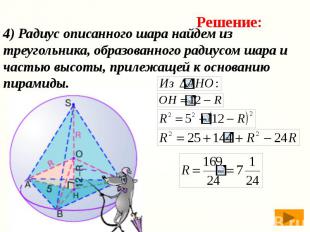
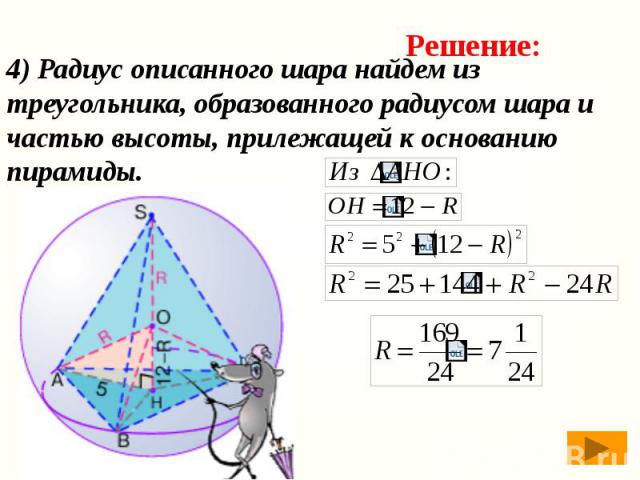
4) Радиус описанного шара найдем из треугольника, образованного радиусом шара и частью высоты, прилежащей к основанию пирамиды.

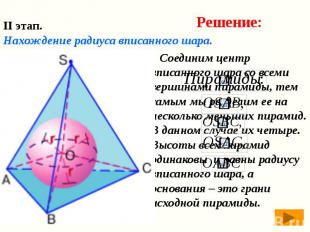
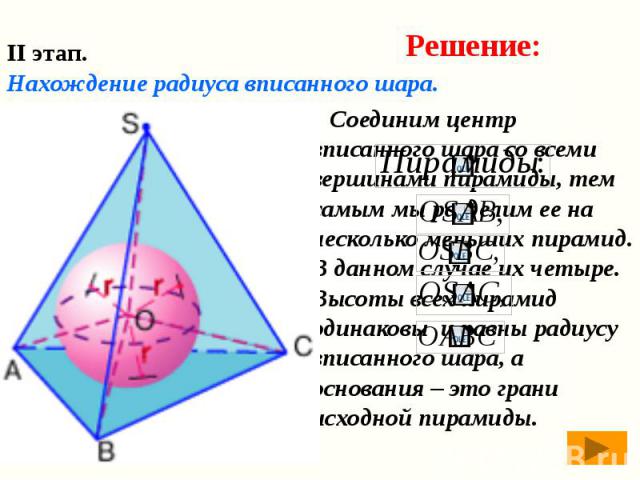
Соединим центр вписанного шара со всеми вершинами пирамиды, тем самым мы разделим ее на несколько меньших пирамид. В данном случае их четыре. Высоты всех пирамид одинаковы и равны радиусу вписанного шара, а основания – это грани исходной пирамиды. Соединим центр вписанного шара со всеми вершинами пирамиды, тем самым мы разделим ее на несколько меньших пирамид. В данном случае их четыре. Высоты всех пирамид одинаковы и равны радиусу вписанного шара, а основания – это грани исходной пирамиды.

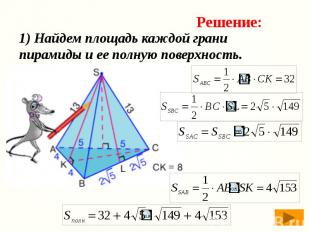
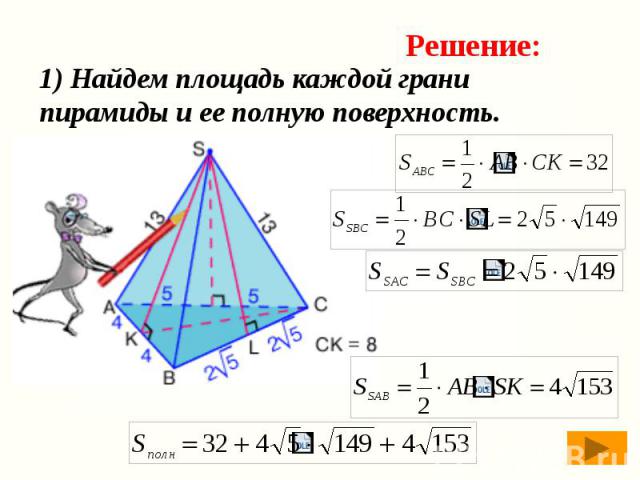
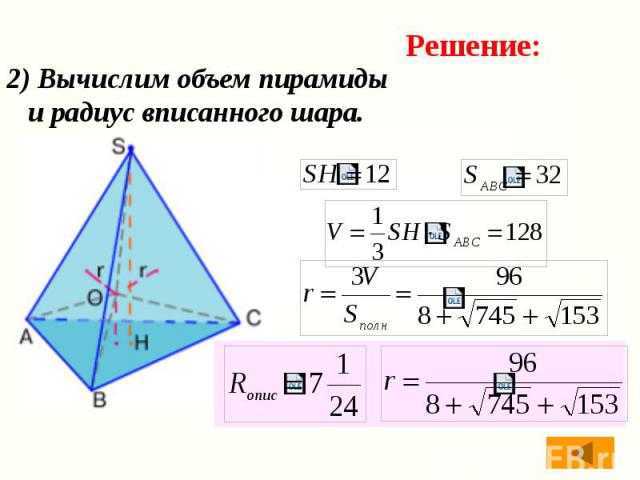
1) Найдем площадь каждой грани пирамиды и ее полную поверхность.

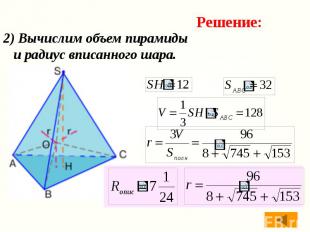
2) Вычислим объем пирамиды и радиус вписанного шара.

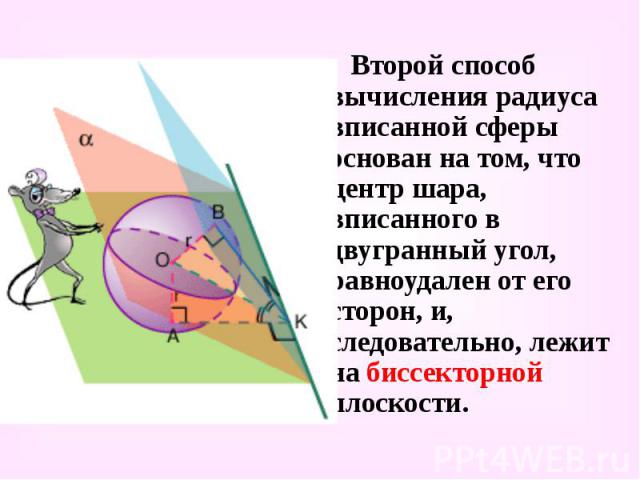
Второй способ вычисления радиуса вписанной сферы основан на том, что центр шара, вписанного в двугранный угол, равноудален от его сторон, и, следовательно, лежит на биссекторной плоскости. Второй способ вычисления радиуса вписанной сферы основан на том, что центр шара, вписанного в двугранный угол, равноудален от его сторон, и, следовательно, лежит на биссекторной плоскости.

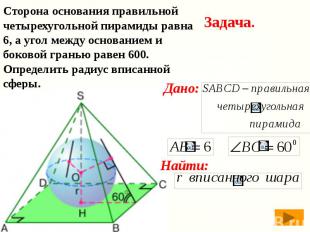
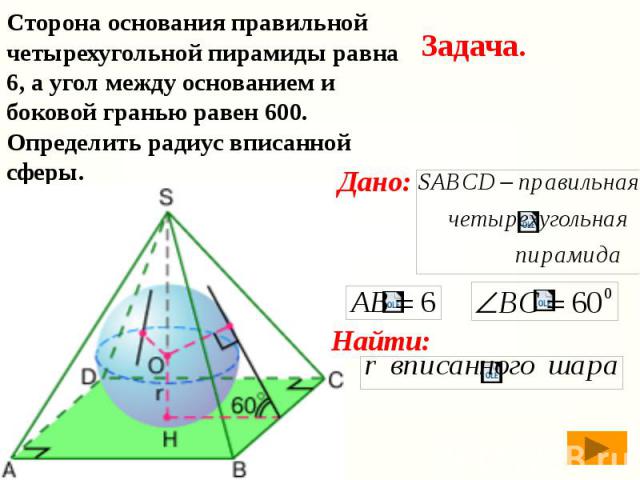
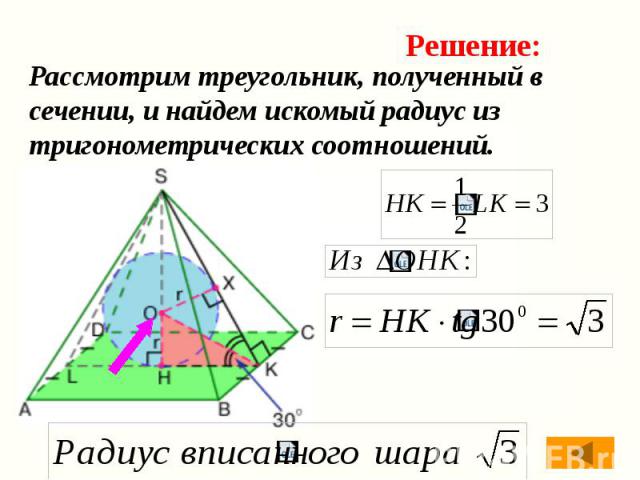
Сторона основания правильной четырехугольной пирамиды равна 6, а угол между основанием и боковой гранью равен 600. Определить радиус вписанной сферы.

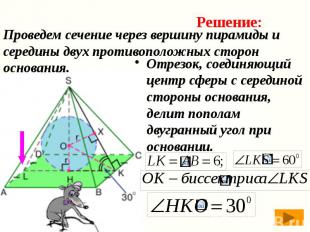
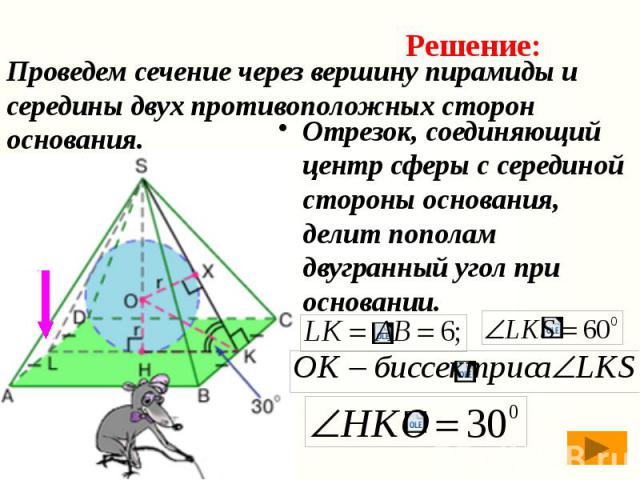
Проведем сечение через вершину пирамиды и середины двух противоположных сторон основания. Отрезок, соединяющий центр сферы с серединой стороны основания, делит пополам двугранный угол при основании.

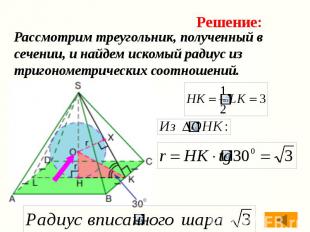
Рассмотрим треугольник, полученный в сечении, и найдем искомый радиус из тригонометрических соотношений.