Презентация на тему: Теорема Пифагора: числа и история

«Теорема Пифагора» Выполнила: Кулясова Ангелина Проверила: учительгеометрии Светлана Петровна

О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским. О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским. Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове. Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет. Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Он поселился в одной из греческих колоний Южной Италии в городе Кротоне. Там Пифагор организовал тайный союз молодёжи из представителей аристократии. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.

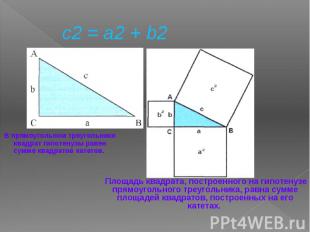
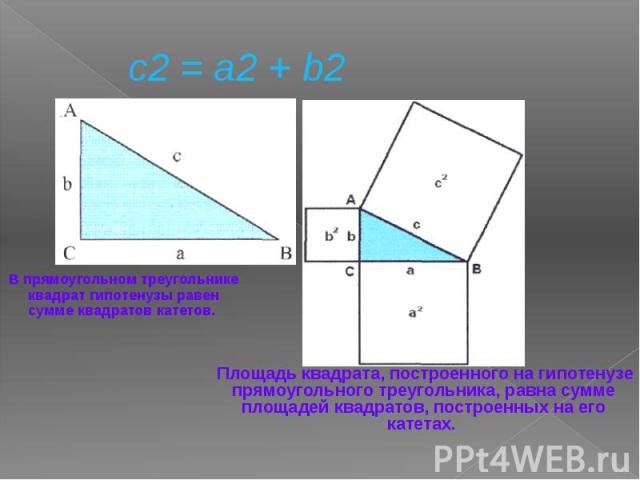
c2 = a2 + b2 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

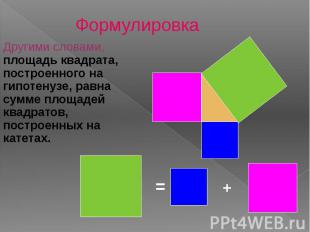
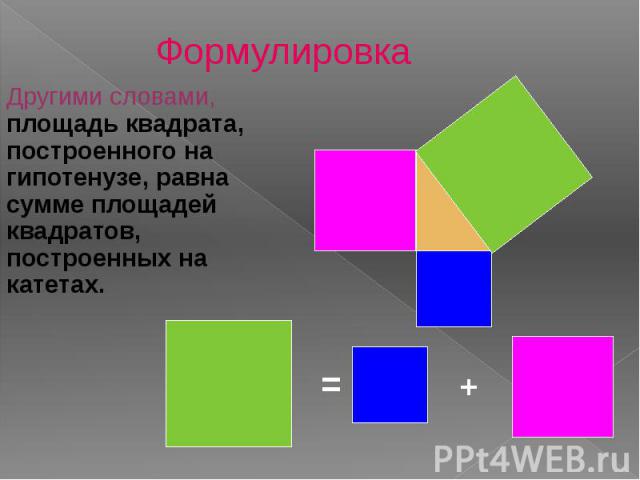
Формулировка Другими словами, площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Формулировка обратной теоремы Теорема, обратная к теореме Пифагора, также справедлива. Она позволяет проверить, является ли тот или иной треугольник прямоугольным. Этим пользовались землемеры и строители Древнего Египта: они размечали прямые углы с помощью веревки, разделенной узлами на 12 равных кусков. Прямоугольный треугольник со сторонами 3, 4, 5 называется «египетским», а тройки (a, b, c) натуральных чисел, удовлетворяющие уравнению c2 = a2 + b2, т. е. служащие длинами сторон прямоугольных треугольников, Пифагоровыми.

Доказательства Доказательства На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии. Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например с помощью дифференциальных уравнений).

Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы (для треугольника АВС квадрат, построенный на гипотенузе АС содержит 4 исходных треугольника, а квадраты, построенные на катетах – по 2 треугольника) Теорема доказана. Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы (для треугольника АВС квадрат, построенный на гипотенузе АС содержит 4 исходных треугольника, а квадраты, построенные на катетах – по 2 треугольника) Теорема доказана.

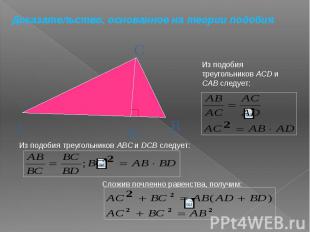
Доказательство Анариция, основанное на том, что равносоставленные фигуры равновелики

Оригинальное доказательство

Доказательство Темпельгофа

Доказательство Хоукинсa

Доказательство индийского математика Бхаскари

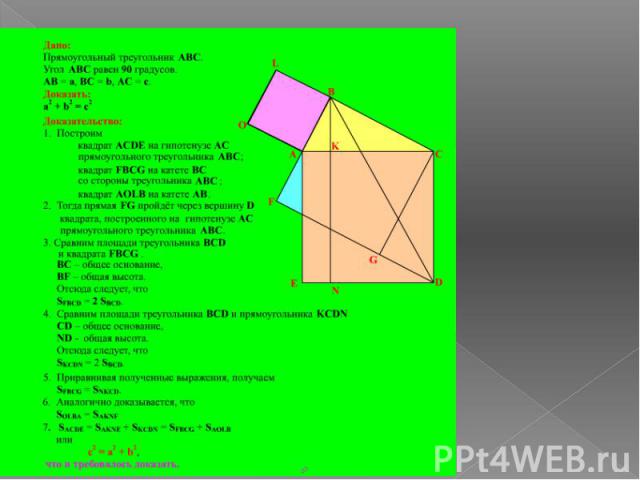
Доказательство Евклида

Историческая справка Пожалуй, это самая популярная теорема геометрии, сделавшая Пифагора наиболее знаменитым математиком. Однако, само утверждение было открыто задолго до него, но в современной истории науки считается, что Пифагор дал ему первое логически стройное доказательство. Теорема Пифагора заслужила место в «Книге рекордов Гиннесса» как получившая наибольшее число доказательств. Американский автор Э. Лумис в книге «Пифагорово предложение», вышедшей в 1940 г., собрал 370 разных доказательств! Однако принципиально различных идей в этих доказательствах используется не так уж много.

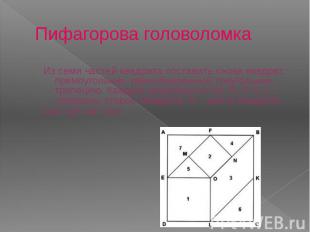
Пифагорова головоломка Из семи частей квадрата составить снова квадрат, прямоугольник, равнобедренный треугольник, трапецию. Квадрат разрезается так: E, F, K, L – середины сторон квадрата, О – центр квадрата, ОМ ḻ EF, NF ḻ EF.

Итак, Итак, Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдём: Катеты в квадрат возводим, Сумму степеней находим – И таким простым путём К результату мы придём. Ч.т.д.

Самое ценное в математике - это возможность быстрого приложения теории к практике