Презентация на тему: Векторы в пространстве

Конкурс интерактивных презентаций «Интерактивная мозаика» Конкурс интерактивных презентаций «Интерактивная мозаика» Pedsovet.su Беляева Ирина Валерьевна МБОУ «Гимназия» г. Верещагино, Пермский край Учитель математики 6-11 класс Первая квалификационная категория

Векторы в пространстве

План изучения темы Вспомним планиметрию «Векторы на плоскости» «Векторы в пространстве»

Тезаурус по теме «Векторы на плоскости» Понятие вектора Направление вектора Равные векторы Коллинеарные вектора Абсолютная величина Действия над векторами Сложение векторов Вычитание векторов

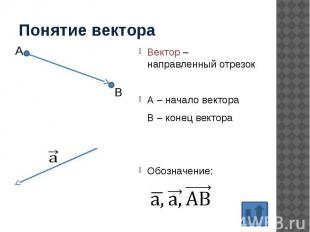
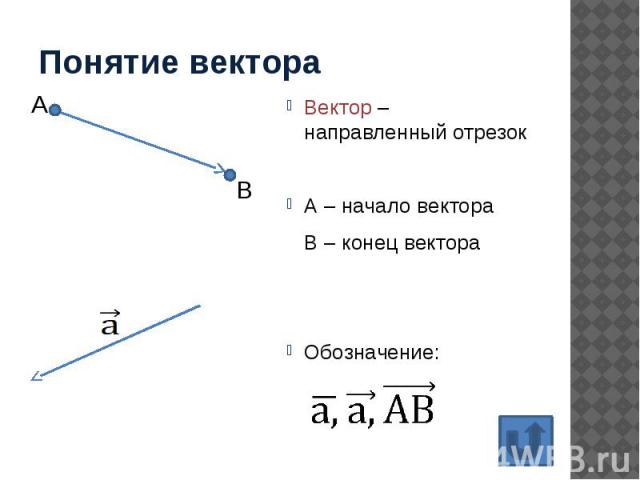
Понятие вектора Вектор – направленный отрезок А – начало вектора В – конец вектора Обозначение:

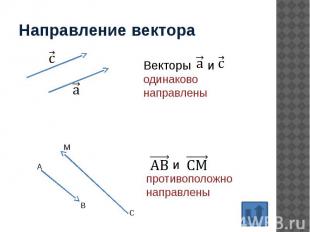
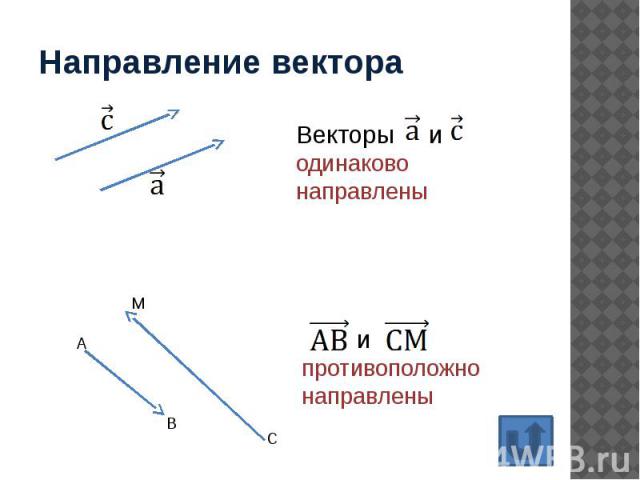
Направление вектора

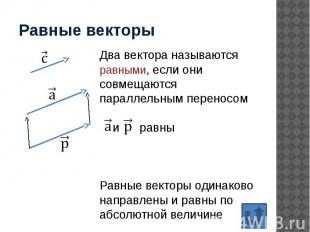
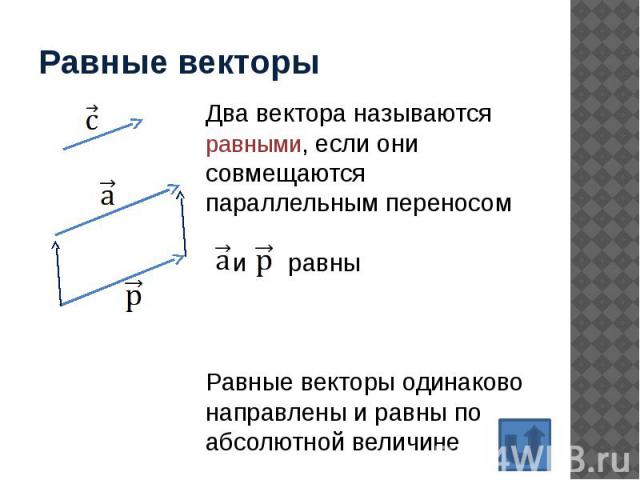
Равные векторы

Коллинеарные вектора Коллинеарные вектора сонаправлены и лежат на параллельных прямых или на одной. , , - коллинеарные =λ∙

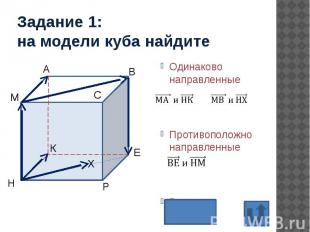
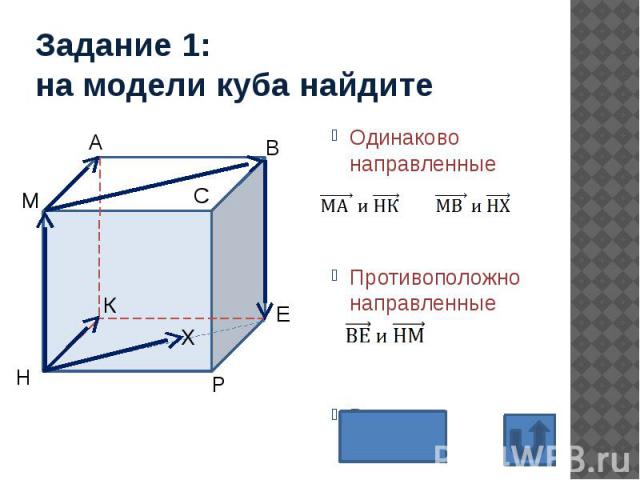
Задание 1: на модели куба найдите Одинаково направленные Противоположно направленные Равные

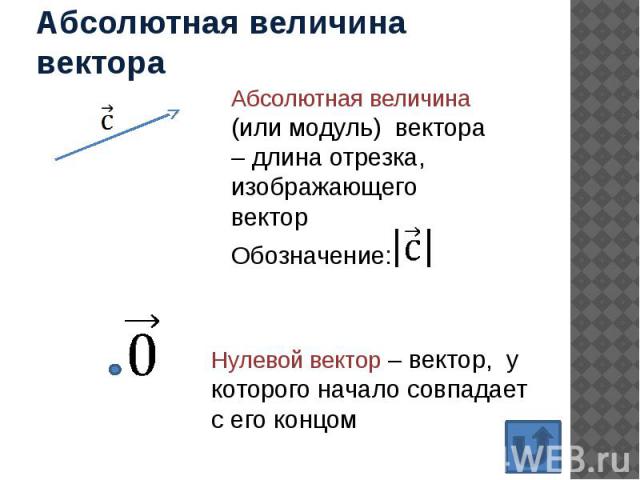
Абсолютная величина вектора

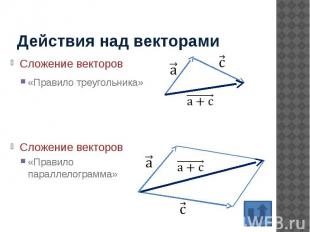
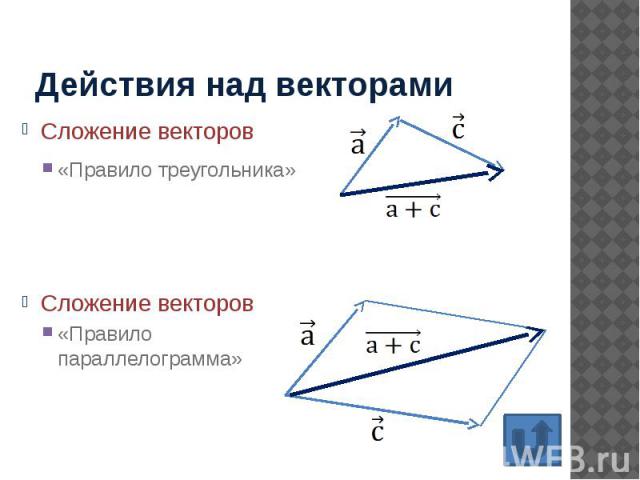
Действия над векторами Сложение векторов «Правило треугольника»

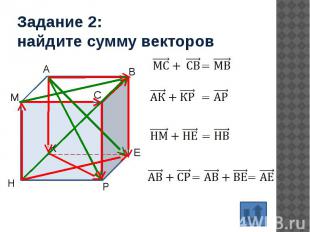
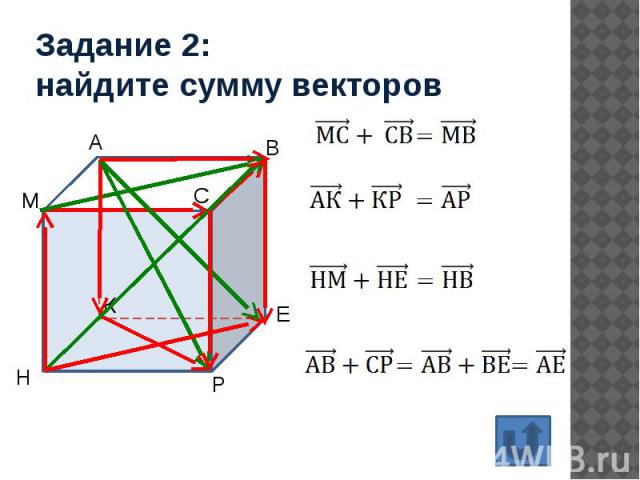
Задание 2: найдите сумму векторов

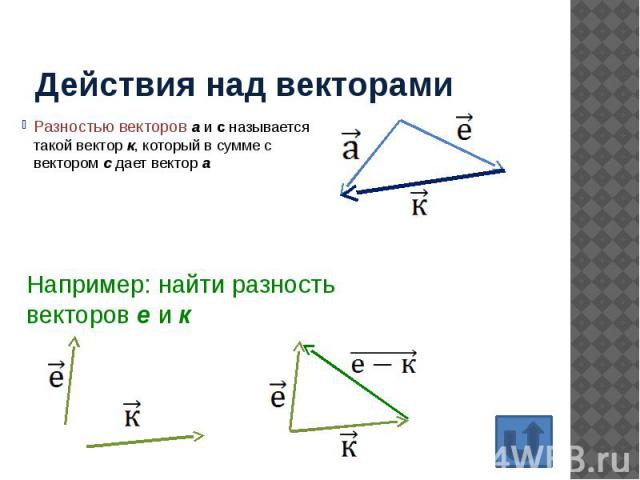
Действия над векторами Разностью векторов а и с называется такой вектор к, который в сумме с вектором с дает вектор а

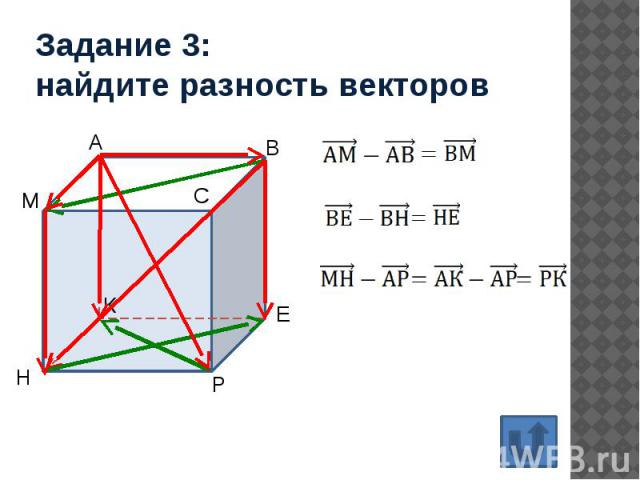
Задание 3: найдите разность векторов

Тезаурус по теме «Векторы в пространстве» Вектор, направление, абсолютная величина Координаты вектора в пространстве Равные вектора Сложение векторов в пространстве Умножение вектора на число Скалярное произведение векторов

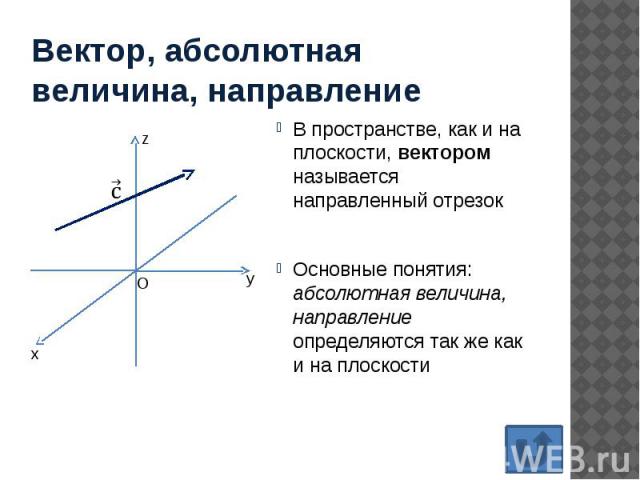
Вектор, абсолютная величина, направление В пространстве, как и на плоскости, вектором называется направленный отрезок Основные понятия: абсолютная величина, направление определяются так же как и на плоскости

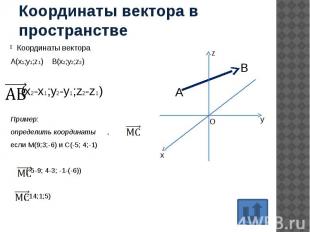
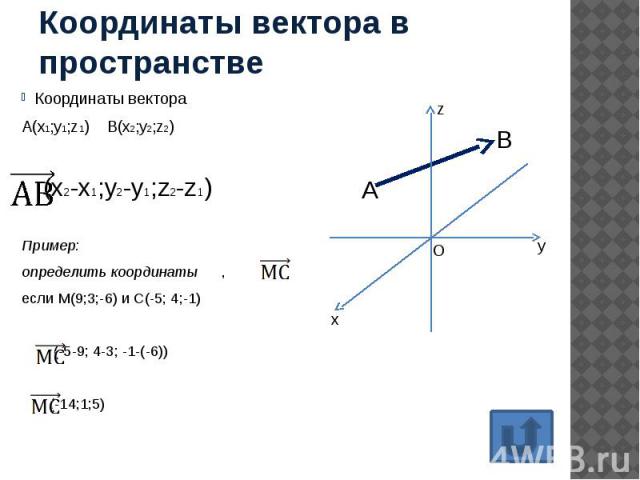
Координаты вектора в пространстве Координаты вектора А(х1;у1;z1) B(x2;y2;z2) (x2-х1;y2-у1;z2-z1) Пример: определить координаты , если М(9;3;-6) и С(-5; 4;-1) (-5-9; 4-3; -1-(-6)) (-14;1;5)

Равные векторы Равные векторы имеют равные соответствующие координаты (х;y;z) (a;b;c) Если х=а,у=b, z=с, то =

Задание 4: укажите пары равных векторов Дано: А(2;7;-3); В(1;0;3); С(-3;-4;5); М(-2;3;-1) Определить: пары равных векторов Решение: Равны соответствующие координаты у векторов , , значит, они попарно равны

Сложение векторов в пространстве Суммой векторов (а;b;с) и (m;n;k) называется вектор (a+m;b+n;c+k) Например, найти координаты вектора , если (-5;3;-9) и (4; -2; 8) Решение: (-5+4; 3+(-2); -9+8) (-1; 1; 1)

Умножение вектора на число Произведением вектора (а;в;с) на число λ называется вектор λ (λа; λв; λс) Например, найти координаты вектора , если (5;-1;-2) Решение:

Скалярное произведение векторов в пространстве Скалярным произведением векторов (а;в;с) и (х;у;z) называется число =ax+вy+cz Например, найти скалярное произведение векторов и Решение:

Задание 5: выполните действия над векторами в пространстве Дано: Найти:

Использовалось учебное пособие автора Погорелова А.П. «Геометрия 10-11». Учебник для общеобразовательных учреждений, М: Просвещение, 2009. Из данного учебного пособия заимствованы рассматриваемые в работе понятия Все рисунки и задачи авторские