Презентация на тему: Теорема о вписанном угле

Теорема о вписанном угле. Урок геометрии. 8 класс

Цели и задачи Ввести понятие вписанного угла. Рассмотреть теорему о вписанном угле и следствия из нее. Показать применение теоремы о вписанном угле и следствий из нее при решении задач. Развивать общеучебные умения и навыки.

Содержание Организационный момент. Актуализация знаний учащихся. Изучение нового материала. Закрепление изученного материала. Подведение итогов урока. Домашнее задание.

Актуализация знаний. Внимательно слушаем одноклассников! 1. Понятие дуги окружности. Дугой окружности называется часть окружности, ограниченная двумя точками, лежащими на окружности. 2.Понятие центрального угла Угол с вершиной в центре окружности называется ее центральным углом. 3.Что называется градусной мерой дуги окружности? *Если дуга ВС окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла ВОС. Если же дуга ВС больше полуокружности, то ее градусная мера считается равной 360˚-уголВОС. Угол с вершиной в центре окружности называется ее центральным углом. 3.Что называется градусной мерой дуги окружности? *Если дуга ВС окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла ВОС. Если же дуга ВС больше полуокружности, то ее градусная мера считается равной 360˚-уголВОС.

Изучение нового материала 1.Определение вписанного угла. 2. Свойство вписанного угла. 3.Следствия из теоремы о вписанном угле. (работа с диском медиатеки РКЦ за №64 «Открытая математика2.6. Планиметрия. ООО « Физикон»

Закрепление изученного материала №653 (устно) из учебника. №654(а-в) полуустно. №655. Решение задач ( работа с диском медиатеки РКЦ за №64 «Открытая математика2.6. Планиметрия. ООО « Физикон») (№1-№4)

Вопросы . 1.Радиус окружности равен 4 см. Можно ли внутри этой окружности поместить треугольник со сторонами 3 см, 6 см, 8,2 см? Нет Да Нельзя определить

Решение. Нет Да Нельзя определить

2.Радиус окружности равен 4 см. Можно ли внутри этой окружности поместить треугольник со сторонами 3 см, 6 см, 8 см? Нет Да Нельзя определить

Решение. Нет Да Нельзя определить

3.Радиус окружности равен 4 см. Можно ли внутри этой окружности поместить треугольник со сторонами 6 см, 6 см, 8 см? Да Нет Нельзя определить

Решение. Да Нет Нельзя определить

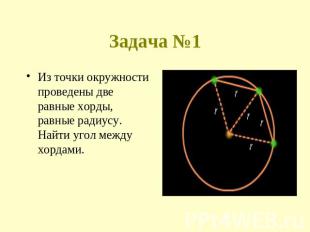
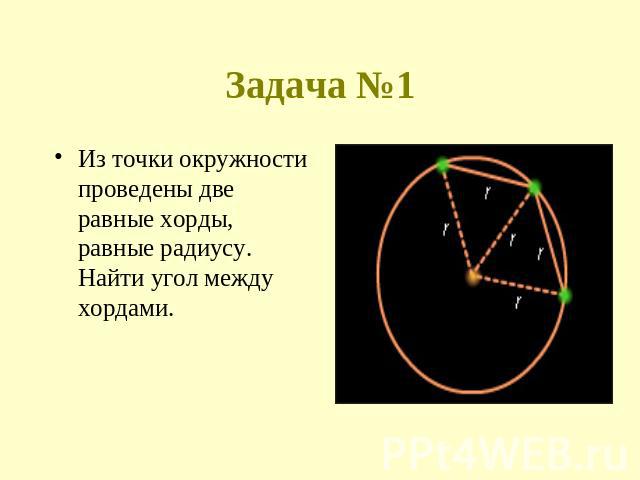
Задача №1 Из точки окружности проведены две равные хорды, равные радиусу. Найти угол между хордами.

Правильный ответ: 120°

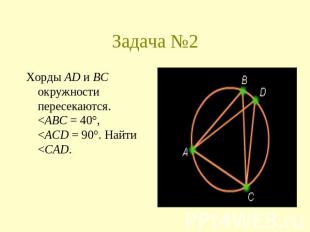
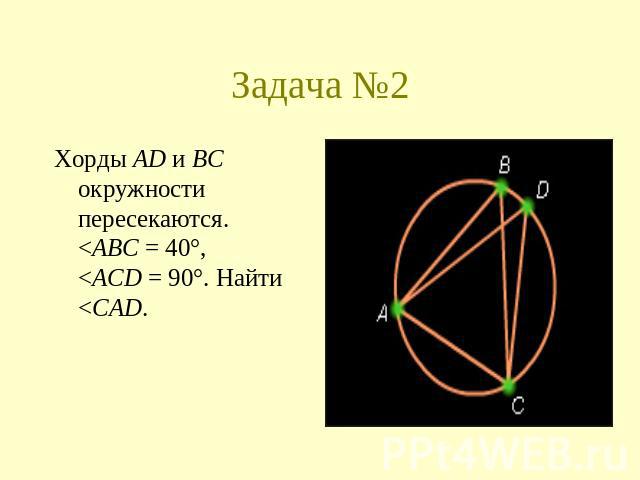
Задача №2 Хорды AD и BC окружности пересекаются. <ABC = 40°, <ACD = 90°. Найти <CAD.

Решение. <ABC = <ADC = 40°. <CAD = 180° – <ADC – <DCA = 50°

Задача №3 Из точки на окружности проведены диаметр и хорда, равная радиусу. Найти угол между ними.

Правильный ответ:  60°

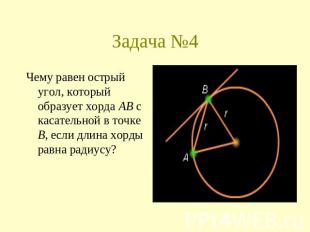
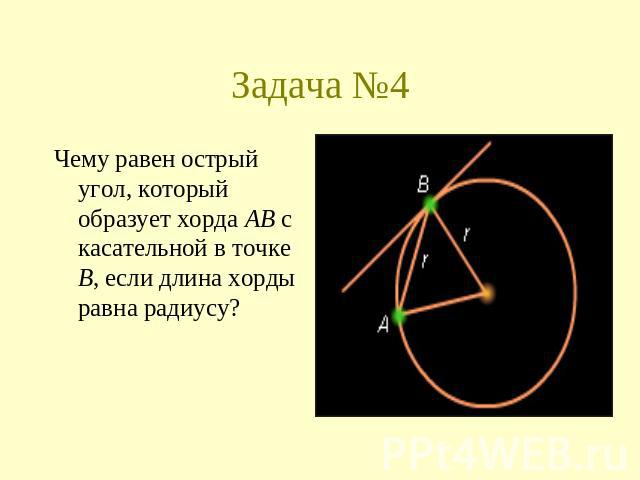
Задача №4 Чему равен острый угол, который образует хорда AB с касательной в точке B, если длина хорды равна радиусу?

Правильный ответ:  30°

Как это называется?

Итог 1.Как называется угол с вершиной в центре окружности? А. Вписанный Б. Центральный В. Развернутый Г. Прямой 2.Как называется угол, вершина которого лежит на окружности, а стороны пересекают окружность? А. Вписанный Б. Центральный В. Смежный Г. Развернутый 3. Вписанный угол равен: А. 90˚ Б. центральному углу В.половине дуги, на которую он опирается Г. дуге, на которую он опирается 4.Вписанный угол, опирающийся на полуокружность , равен: А. 180 ˚ Б. 360 ˚В. 50˚ Г. 90˚

Проверь себя

Домашнее задание Выучить п .71 ( до второй теоремы). Решить задачи :№654 (г), №656.

Спасибо за работу!

Урок разработан учителем математики Венскович Аллой Сергеевной МОУ СОШ п. Пяльма Пудожского района Республики Карелия

Использованные ресурсы Учебник геометрии 7-9 под редакцией Атанасян Л.С. диск медиатеки РКЦ за №64 «Открытая математика2.6. Планиметрия. ООО « Физикон»