Презентация на тему: Теорема о вписанном угле 8 класс

Теорема о вписанном угле

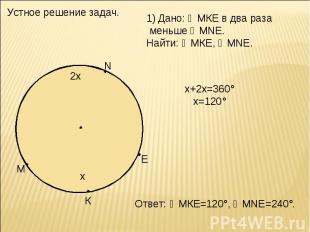
Устное решение задач. Дано: ◡МКЕ в два раза меньше ◡MNE. Найти: ◡МКЕ, ◡MNE. х+2х=360° х=120° Ответ: ◡МКЕ=120°, ◡MNE=240°.

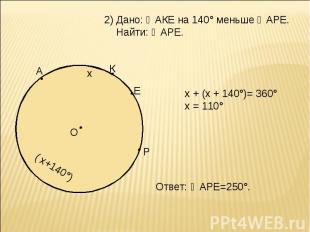
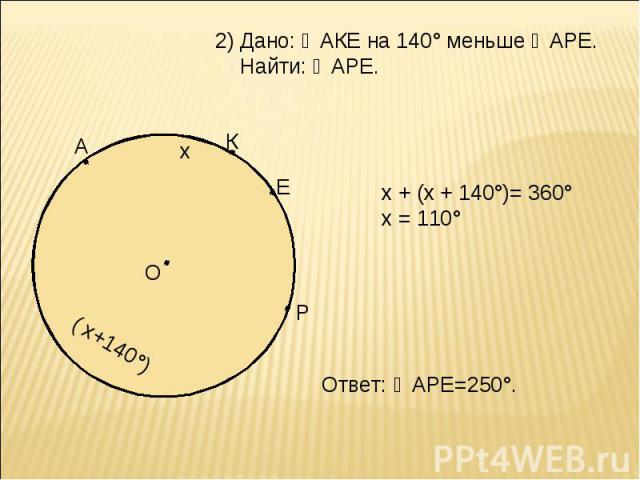
Дано: ◡АКЕ на 140° меньше ◡АРЕ. Найти: ◡АРЕ. х + (х + 140°)= 360° х = 110° Ответ: ◡АРЕ=250°.

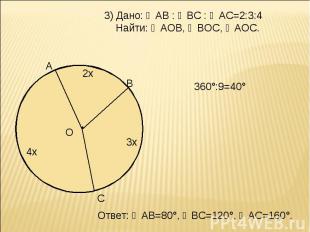
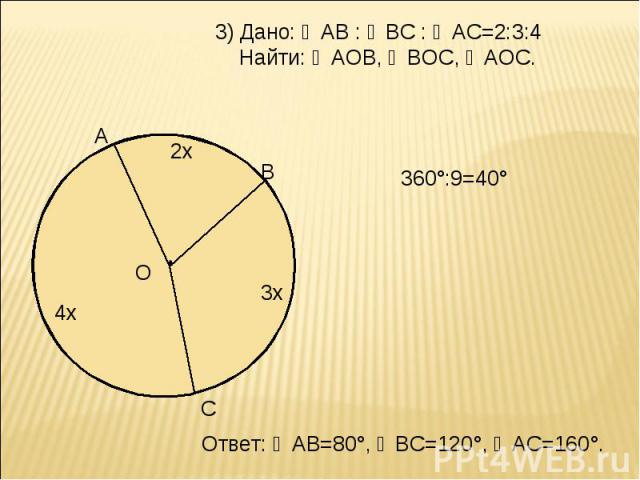
3) Дано: ◡АВ : ◡ВС : ◡АС=2:3:4 Найти: ∠АОВ, ∠ВОС, ∠АОС. 360°:9=40° Ответ: ◡АВ=80°, ◡ВС=120°, ◡АС=160°.

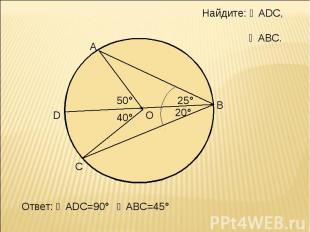
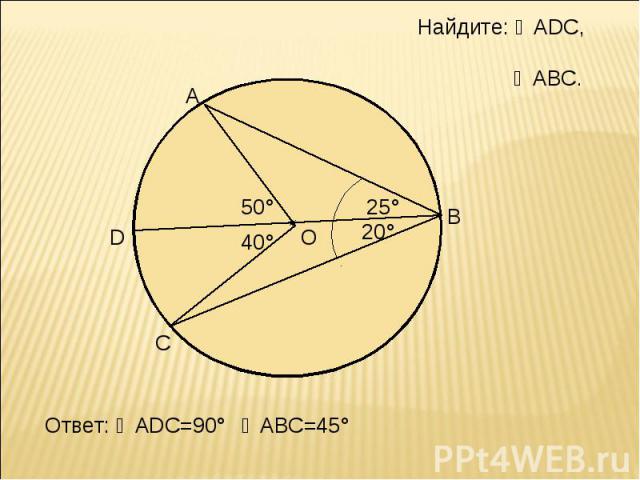
Найдите: ◡АDС, ∠АВС. Ответ: ◡АDС=90°

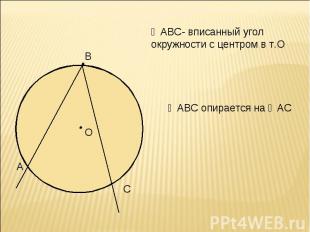
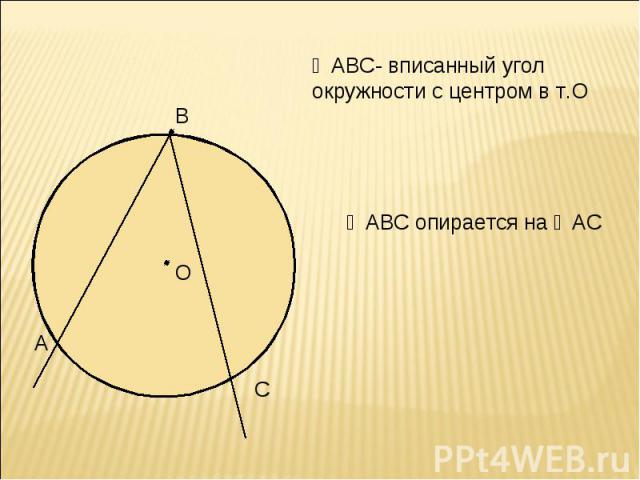
∠АВС- вписанный угол окружности с центром в т.О ∠АВС опирается на ◡АС

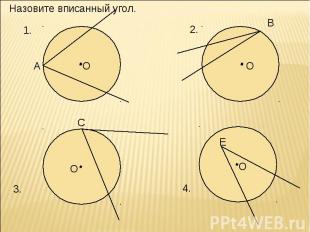
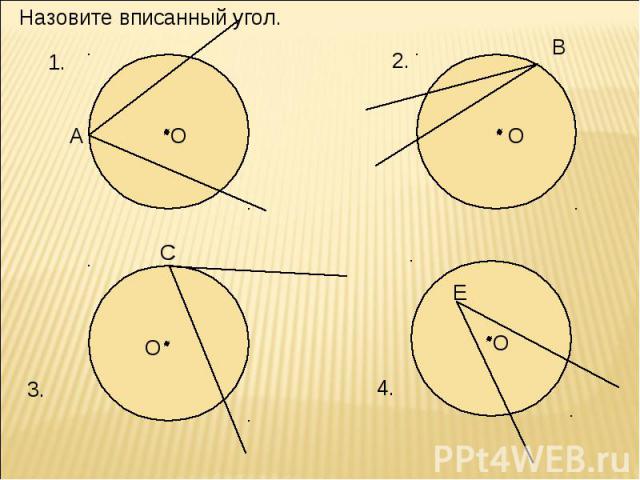
Назовите вписанный угол.

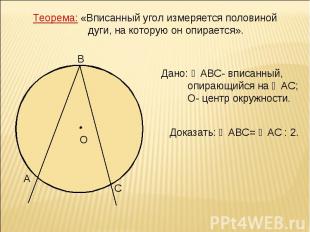
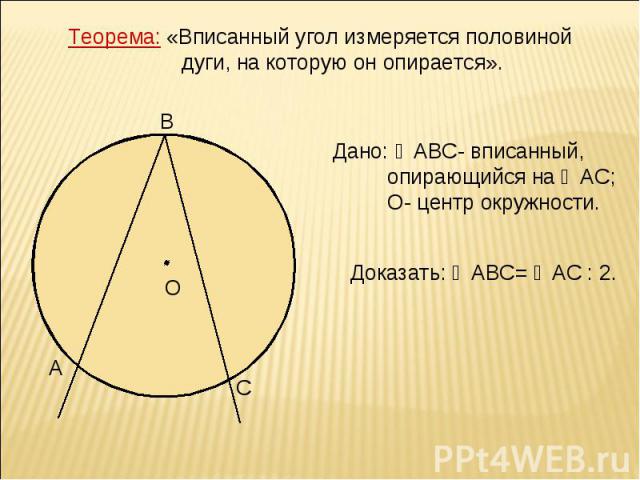
Теорема: «Вписанный угол измеряется половиной дуги, на которую он опирается». Дано: ∠АВС- вписанный, опирающийся на ◡АС; О- центр окружности. Доказать: ∠АВС= ◡АС : 2.

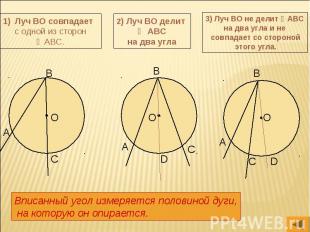
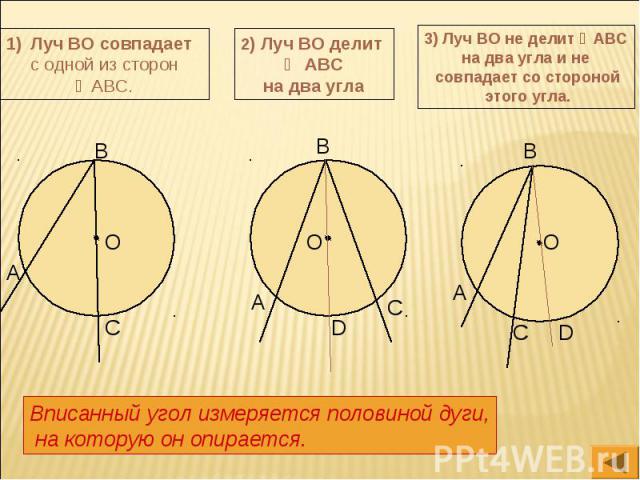
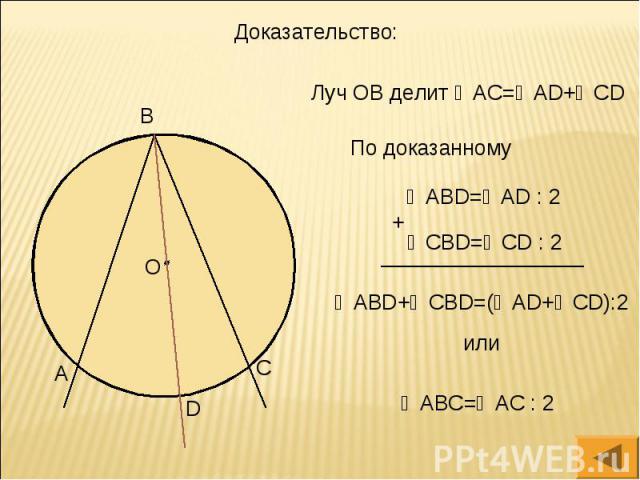
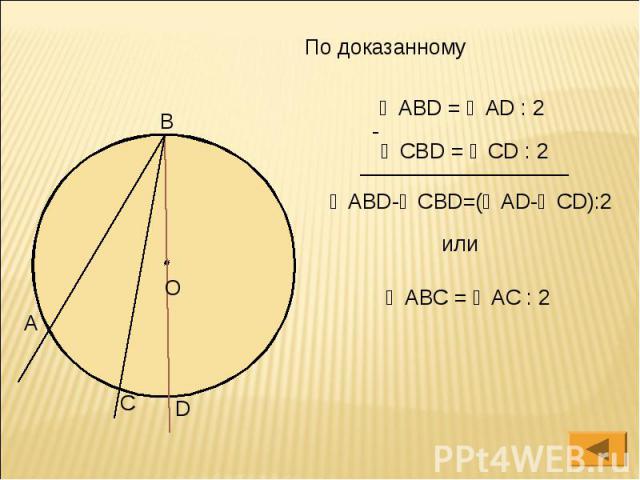
Луч ВО совпадает с одной из сторон ∠АВС. 2) Луч ВО делит ∠ АВС на два угла 3) Луч ВО не делит ∠АВС на два угла и не совпадает со стороной этого угла. Вписанный угол измеряется половиной дуги, на которую он опирается.

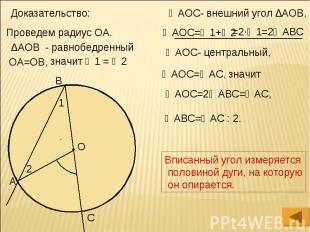
Вписанный угол измеряется половиной дуги, на которую он опирается.

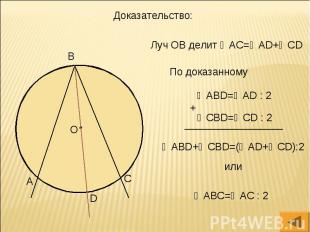
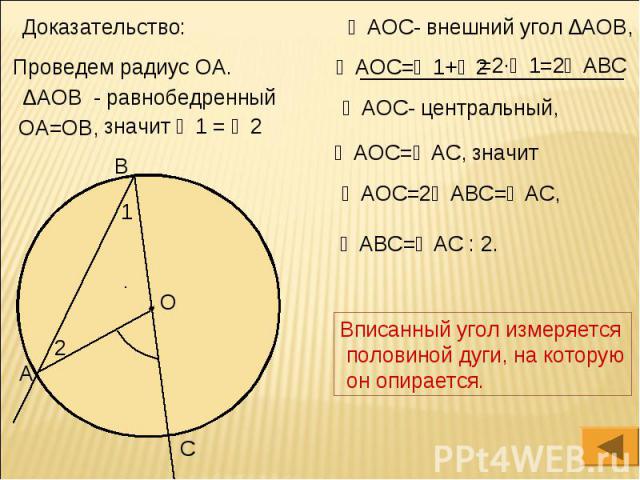
Доказательство:

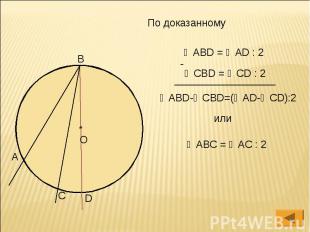
По доказанному

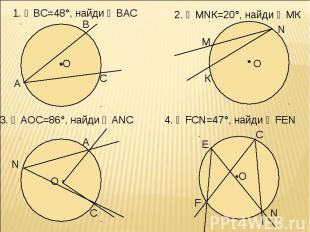
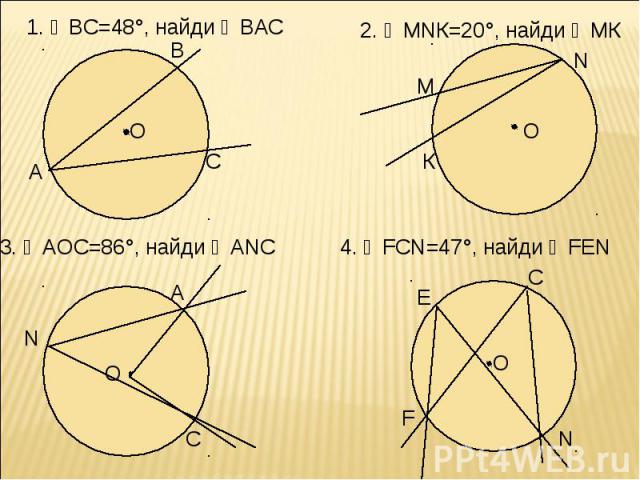
1. ◡ВС=48°, найди ∠ВАС 2. ∠МNК=20°, найди ◡МК 3. ∠АОС=86°, найди ∠АNC 4. ∠FCN=47°, найди ∠FEN

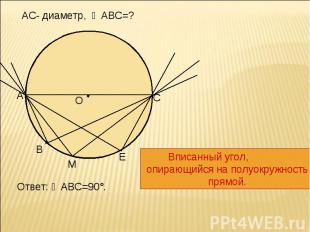
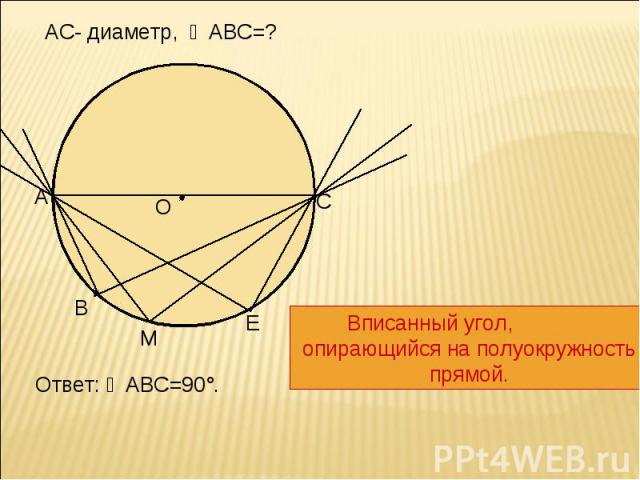
АС- диаметр, ∠АВС=? Вписанный угол, опирающийся на полуокружность прямой.

Решение задач:

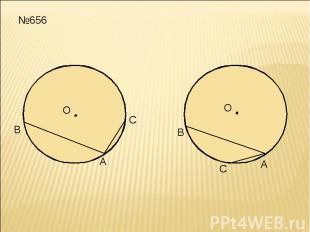
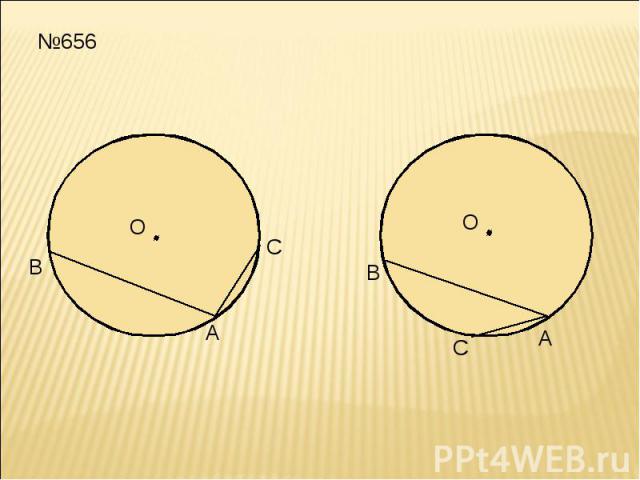
№656

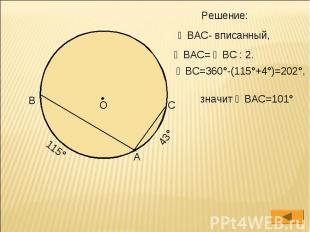
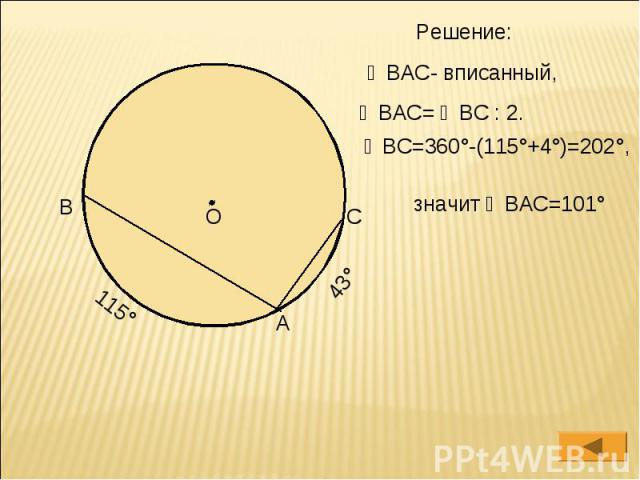
Решение: ∠ВАС- вписанный, ∠ВАС= ◡ВС : 2. ◡ВС=360°-(115°+4°)=202°, значит ∠ВАС=101°

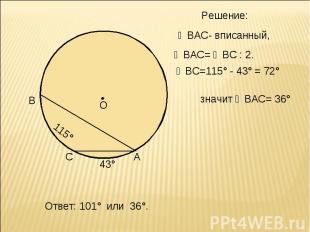
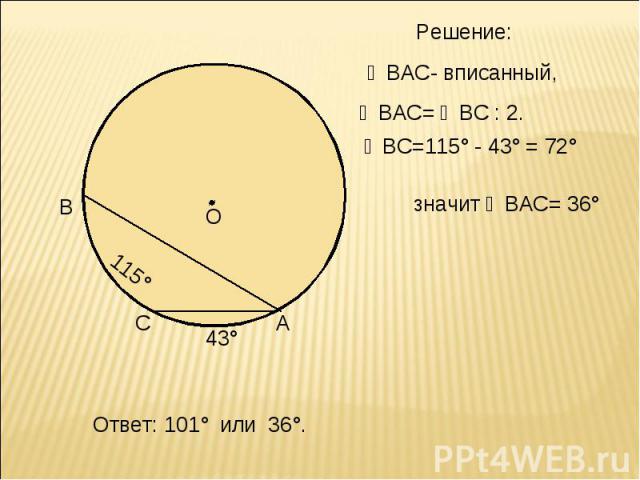
Решение: ∠ВАС- вписанный, ∠ВАС= ◡ВС : 2. ◡ВС=115° - 43° = 72° значит ∠ВАС= 36° Ответ: 101° или 36°.

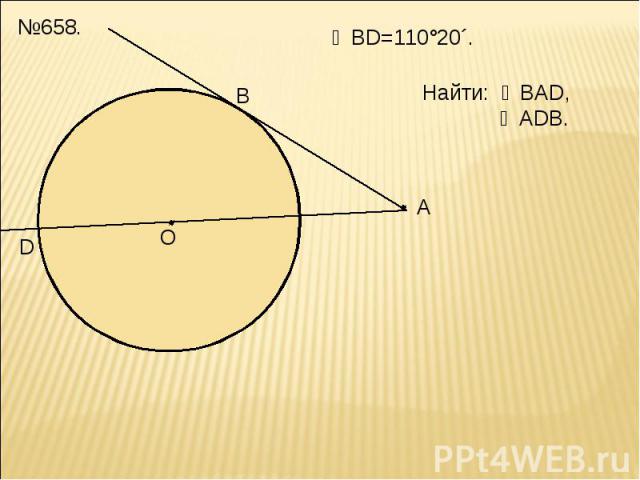
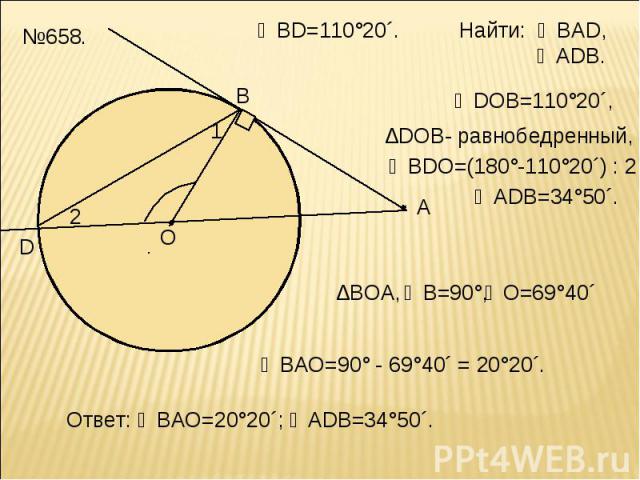
№658.

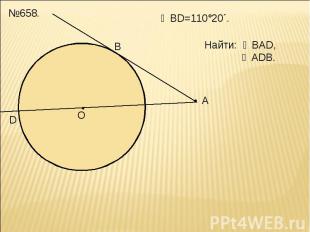
◡BD=110°20´. Найти: ∠ВAD, ∠ADB.

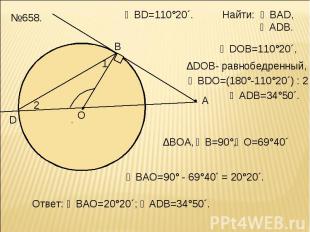
◡BD=110°20´. Найти: ∠ВAD, ∠ADB. ∆DOB- равнобедренный,

Домашнее задание: п.71