Презентация на тему: Сферическая поверхность. Шар 11 класс

Сферическая поверхность. Шар Геометрия 11 класс Р.О.Калошина, ГОУ лицей №533 Санкт-Петербург

Содержание Сферическая поверхность Уравнение сферы Взаимное расположение сферы и плоскости Касательная плоскость к сфере Площадь сферы, объем шара Вопросы

Сферическая поверхность Сферической поверхностью называется геометрическое место точек пространства, равноудаленных от одной точки – центра. Тело, ограниченное сферической поверхностью, называется шаром.

Сферическая поверхность (продолжение) O – центр сферы R – радиус сферы Ось – любая прямая, проходящая через центр сферы

Уравнение сферы В прямоугольной системе координат уравнение сферы радиуса R с центром C (xo;yo;zo) имеет вид: (x-xo)²+(y-yo)²+(z-zo)²=R²

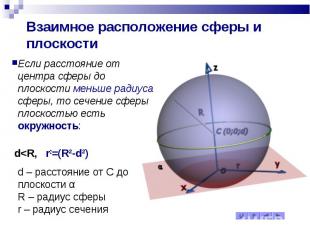
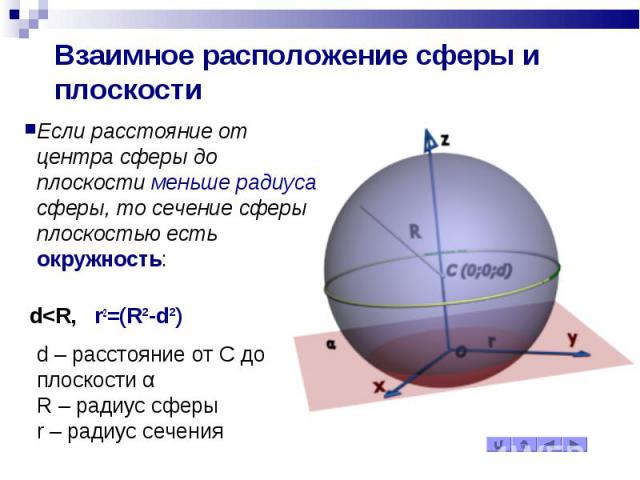
Взаимное расположение сферы и плоскости Если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность: d

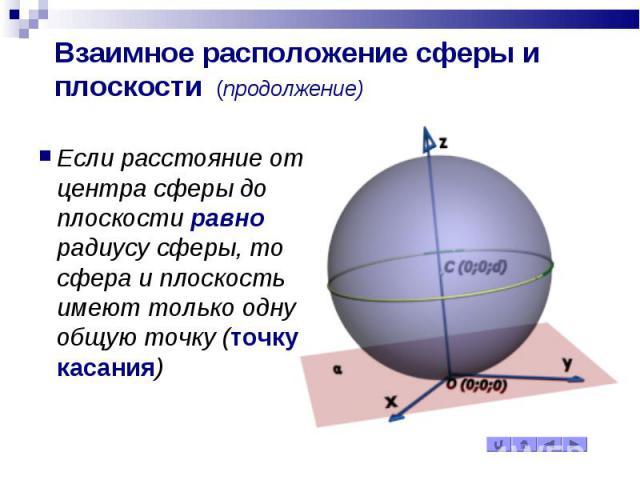
Взаимное расположение сферы и плоскости (продолжение) Если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку (точку касания)

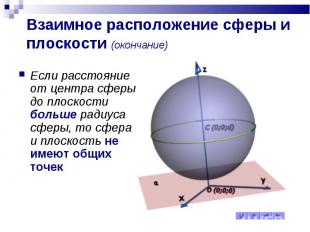
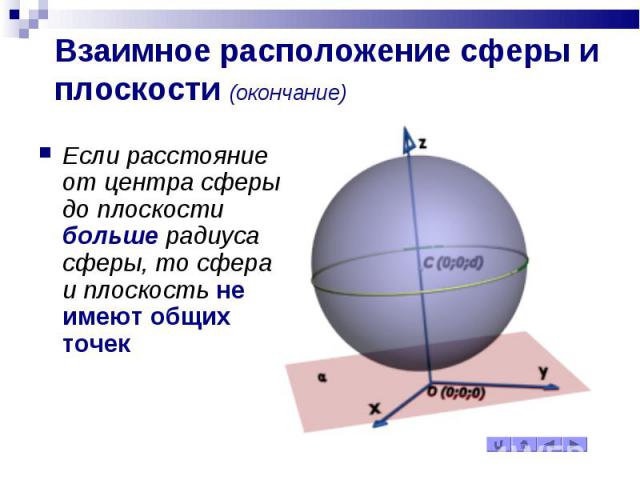
Взаимное расположение сферы и плоскости (окончание) Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек

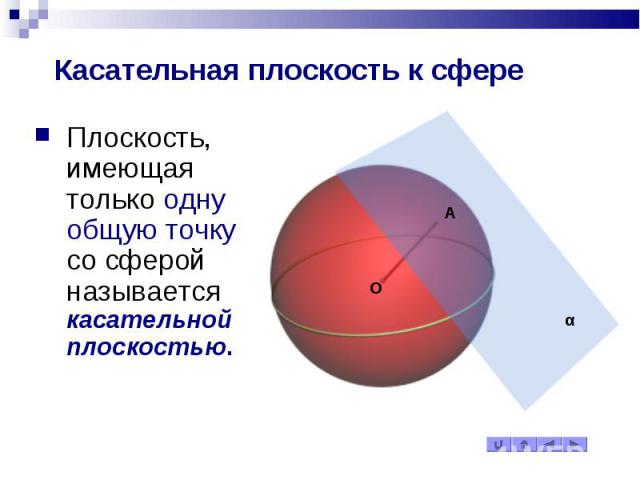
Касательная плоскость к сфере Плоскость, имеющая только одну общую точку со сферой называется касательной плоскостью.

Касательная плоскость к сфере (продолжение) Теорема: Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости. Обратная теорема: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

Площадь сферы, объем шара (продолжение) Теорема Архимеда Объем шара в полтора раза меньше объема описанного вокруг него цилиндра, а площадь поверхности шара в полтора раза меньше площади полной поверхности того же цилиндра: V= (2/3)V1 S= (2/3)S1 где V1 – объем описанного цилиндра, S1 – площадь полной поверхности этого цилиндра

Площадь сферы, объем шара Площадь поверхности шара радиуса R равна учетверенной площади большого круга: S=4pR² Объем шара радиуса R равен V = (4/3)pR³

Вопросы для закрепления Дайте определение сферы, шара. Можно ли рассматривать сферу как поверхность вращения, а шар – как тело вращения? Что называется: а) центром сферы; б) радиусом сферы? Сколько центров симметрии имеет сфера? Сколько осей симметрии имеет сфера? Какая плоскость наз. касательной к сфере? Какой вид имеет уравнение сферы?