Презентация на тему: Решение задач на применение первого признака равенства треугольников

Решение задач на применение первого признака равенства треугольников МОУ ООШ Д. Старое Мелково Учитель: Костик Инна Станиславовна

Цель урока Совершенствование навыков решения задач на применение первого признака равенства треугольников; Закрепление умения доказывать теоремы.

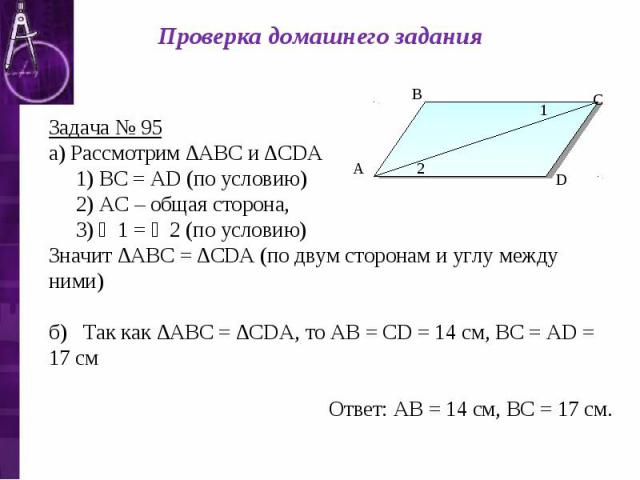
Проверка домашнего задания Задача № 95 а) Рассмотрим ∆АВС и ∆СDА 1) ВС = АD (по условию) 2) АС – общая сторона, 3) ∠1 = ∠2 (по условию) Значит ∆АВС = ∆СDА (по двум сторонам и углу между ними) б) Так как ∆АВС = ∆СDА, то АВ = СD = 14 см, ВС = АD = 17 см Ответ: АВ = 14 см, ВС = 17 см.

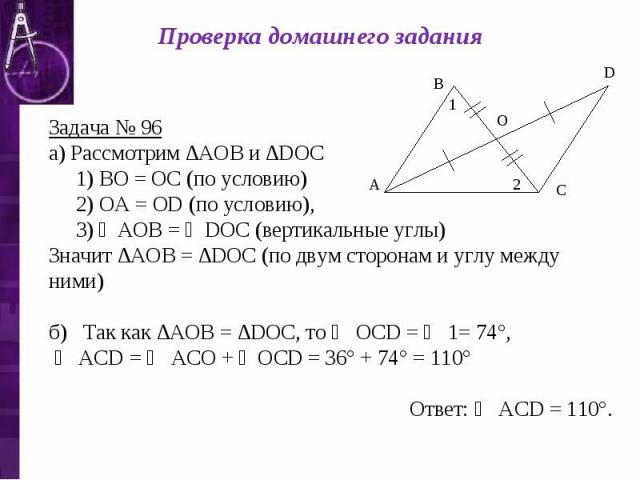
Проверка домашнего задания Задача № 96 а) Рассмотрим ∆АОВ и ∆DОС 1) ВО = ОС (по условию) 2) ОА = ОD (по условию), 3) ∠АОВ = ∠DОС (вертикальные углы) Значит ∆АОВ = ∆DОС (по двум сторонам и углу между ними) б) Так как ∆АОВ = ∆DОС, то ∠ ОСD = ∠ 1= 74°, ∠ АСD = ∠ АСО + ∠ОСD = 36° + 74° = 110° Ответ: ∠ АСD = 110°.

Проверка домашнего задания а) Рассмотрим ∆АОВ и ∆DОС 1) ВО = ОС (по условию) 2) ОА = ОD (по условию), 3) ∠АОВ = ∠DОС (вертикальные углы) Значит ∆АОВ = ∆DОС (по двум сторонам и углу между ними) б) Так как ∆АОВ = ∆DОС, то ∠ ОСD = ∠ 1= 74°, ∠ АСD = ∠ АСО + ∠ОСD = 36° + 74° = 110° Ответ: ∠ АСD = 110°.

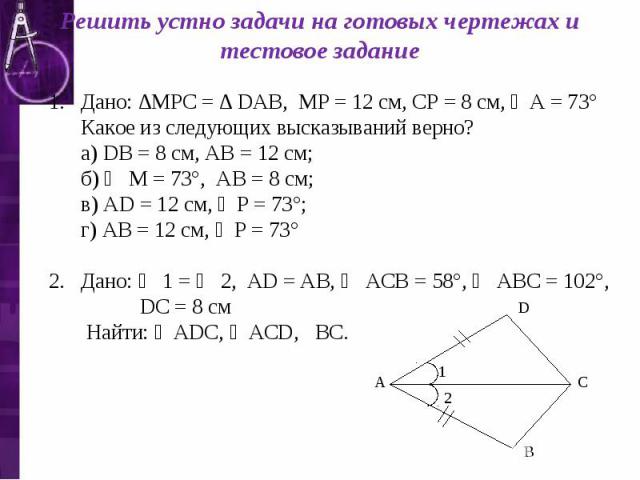
Решить устно задачи на готовых чертежах и тестовое задание Дано: ∆МРС = ∆ DАВ, МР = 12 см, СР = 8 см, ∠А = 73° Какое из следующих высказываний верно? а) DВ = 8 см, АВ = 12 см; б) ∠ М = 73°, АВ = 8 см; в) АD = 12 см, ∠Р = 73°; г) АВ = 12 см, ∠Р = 73° Дано: ∠ 1 = ∠ 2, АD = АВ, ∠ АСВ = 58°, ∠ АВС = 102°, DС = 8 см Найти: ∠АDС, ∠АСD, ВС.

Решить устно задачи на готовых чертежах и тестовое задание Дано: ВС = АD, ∠ 1 = ∠ 2, ∠ АСD = 42°, ∠ АDС = 108°, DС = 6 см Найти: ∠САВ, ∠АВС, АВ. Решить задачи из рабочей тетради № 56 – 59

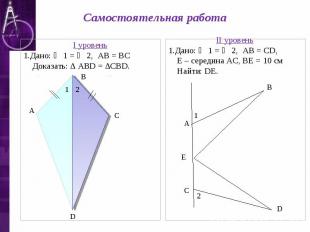
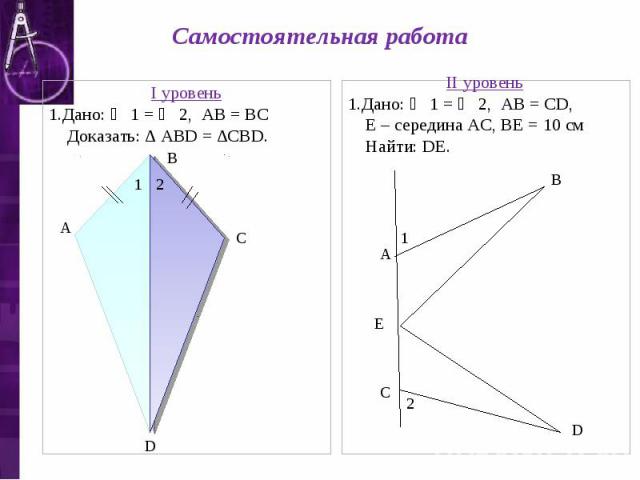
Самостоятельная работа I уровень 1.Дано: ∠ 1 = ∠ 2, АВ = ВС Доказать: ∆ АВD = ∆СВD. II уровень 1.Дано: ∠ 1 = ∠ 2, АВ = СD, Е – середина АС, ВЕ = 10 см Найти: DЕ.

Домашнее задание п. 15 учебник № 97, 98, 99