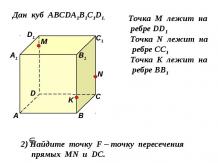
Презентация на тему: Теорема о вписанном угле

Теорема о вписанном угле

Какая дуга называется полуокружностью?Какой угол называется центральным?Как находится дуга, если она меньше полуокружности?Как находится дуга, если она больше полуокружности?

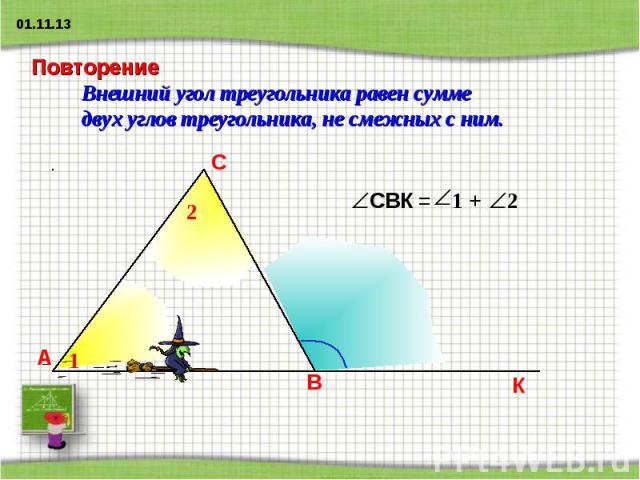
Повторение Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

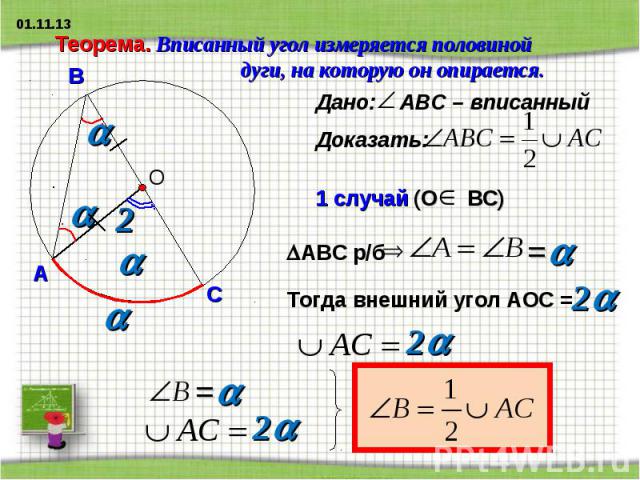
Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается.

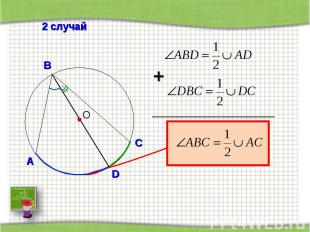
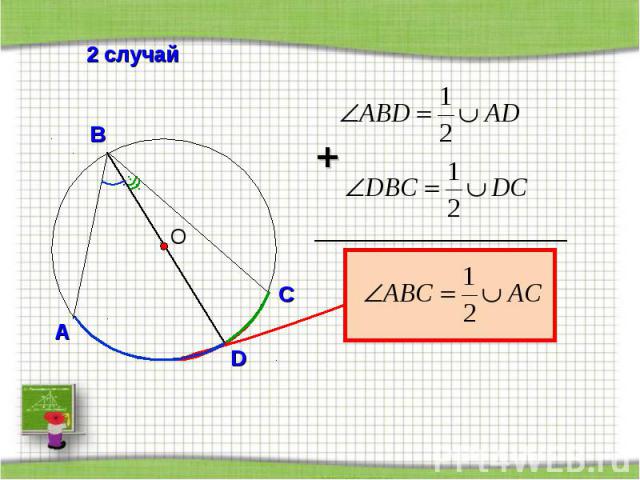
2 случай

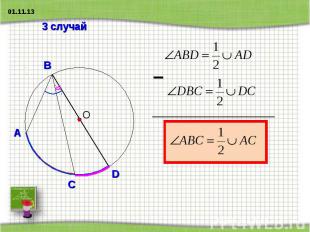
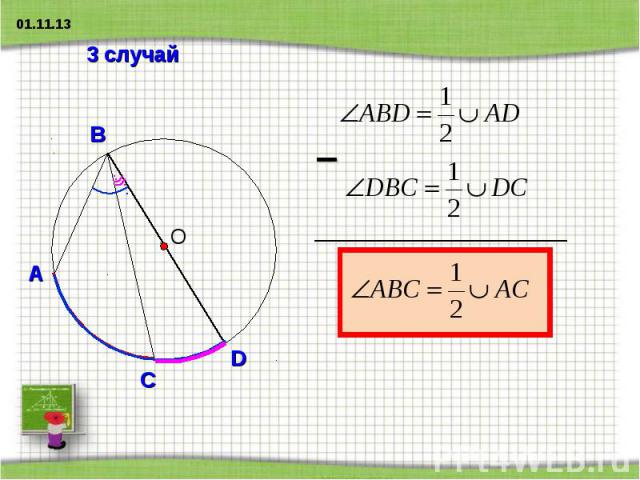
3 случай

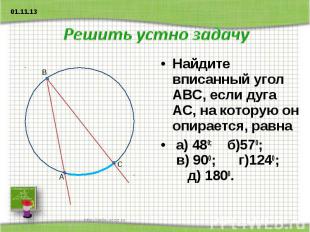
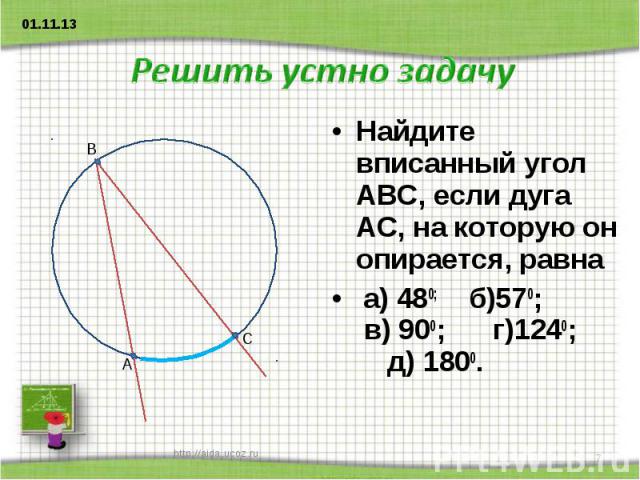
Решить устно задачу Найдите вписанный угол АВС, если дуга АС, на которую он опирается, равна а) 480; б)570; в) 900; г)1240; д) 1800.

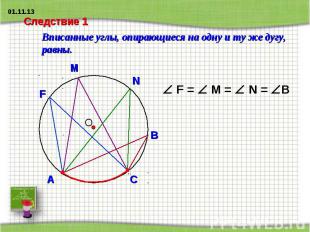
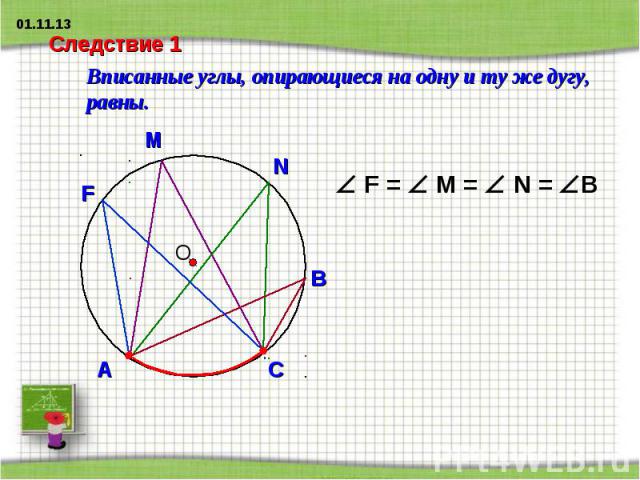
Следствие 1 Вписанные углы, опирающиеся на одну и ту же дугу, равны.

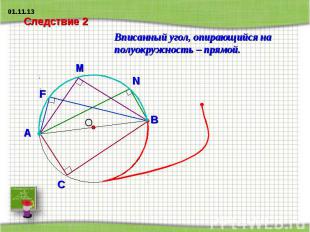
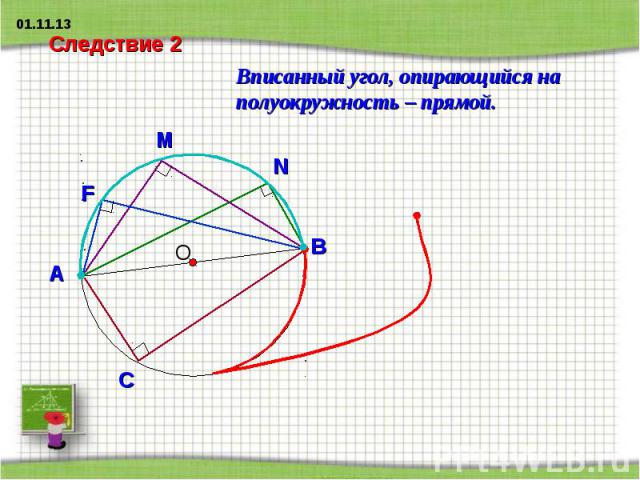
Следствие 2Вписанный угол, опирающийся на полуокружность – прямой.

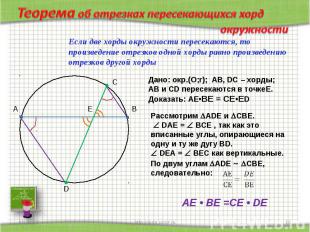
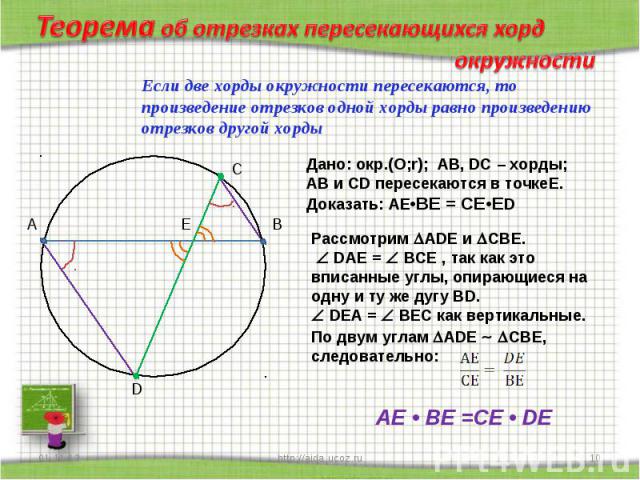
Теорема об отрезках пересекающихся хорд окружности Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хордыДано: окр.(О;r); АВ, DC – хорды; АВ и СD пересекаются в точкеЕ.Доказать: АЕ•ВЕ = СЕ•ЕD Рассмотрим АDЕ и СВЕ. DАЕ = ВСЕ , так как это вписанные углы, опирающиеся на одну и ту же дугу ВD. DЕА = ВЕС как вертикальные.По двум углам АDЕ СВЕ, следовательно: АЕ • ВЕ =СЕ • DE

Использованная литература Геометрия, 7-9: учеб.для общеобразовательных учреждений/(Л.С.Атанасян, В.Ф.Бутузов и др) М.: Просвещение, 2007. Шаблон презентации и анимированные картинки – ресурсы Интернета