Презентация на тему: Преобразования на плоскости

Преобразования на плоскости МОУ СОШ № 5 г. Ивантеевка учитель математики Любецкая Н. Ф.

О симметрия! Гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, в малой мошке, Ты в елочке, что у лесной дорожки. С тобою в дружбе и тюльпан, и роза, И снежный рой – творение мороза!

Симметрия (греч.) - соразмерность, пропорциональность, одинаковость в расположении частей.

Виды симметрии Симметрия относительно прямой Симметрия относительно точки Поворот Симметрия в природе Симметрия в архитектуре

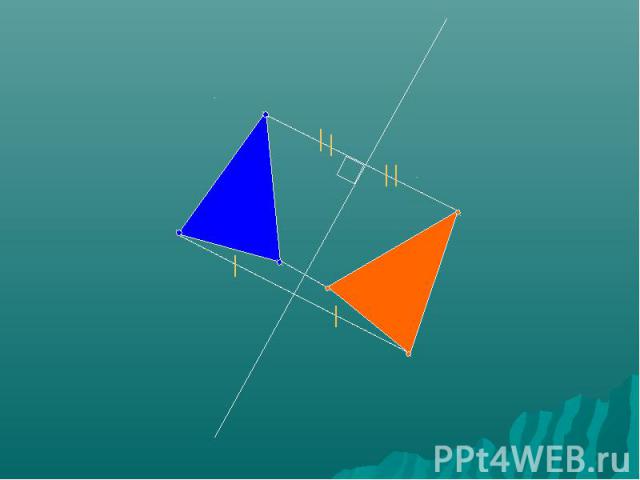
Симметрия относительно прямой – осевая симметрия Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему

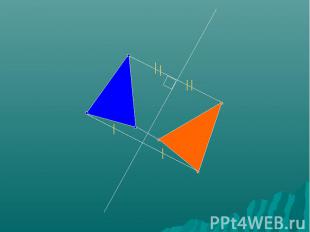
Являются ли данные точки симметричными ?

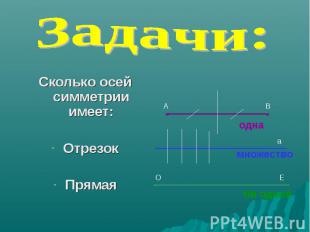
Задачи: Сколько осей симметрии имеет: Отрезок Прямая Луч

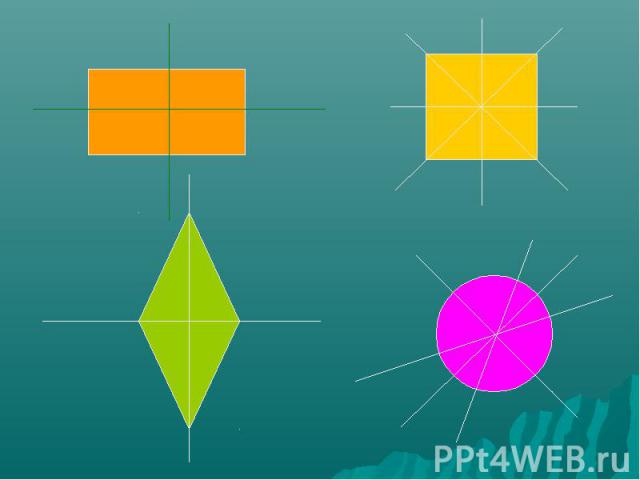
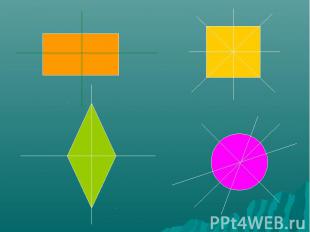
Какие из этих фигур имеют ось симметрии? Сколько осей симметрии имеет каждая фигура?

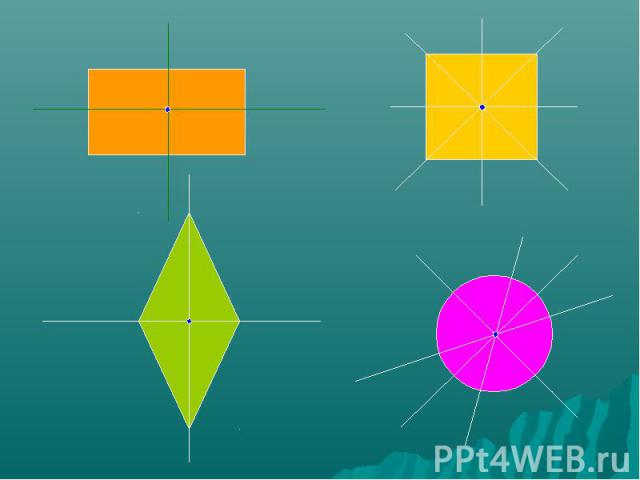
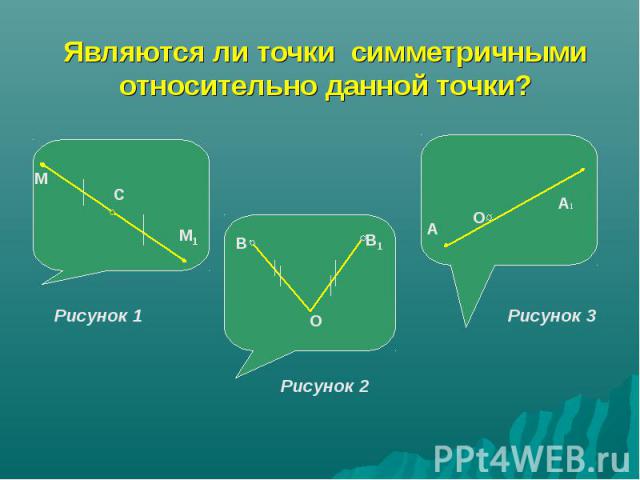
Симметрия относительно точки- центральная симметрия Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1 О - центр симметрии

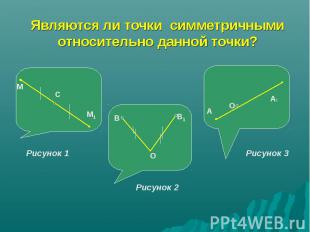
Являются ли точки симметричными относительно данной точки?

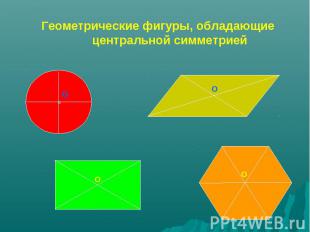
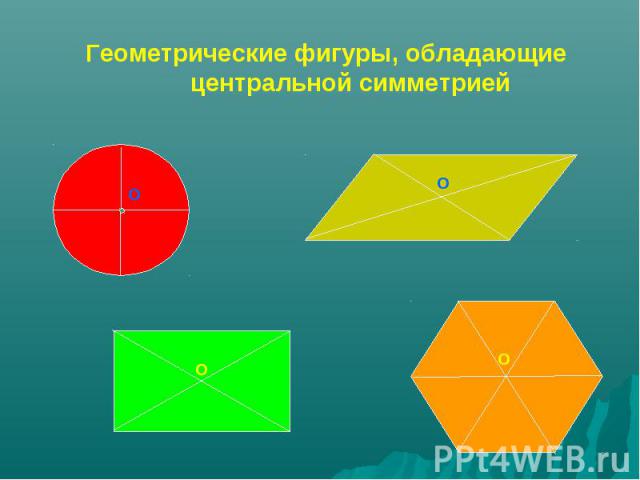
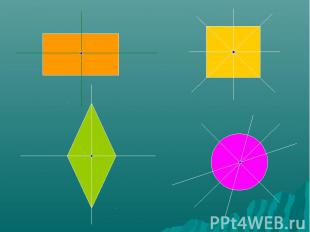
Геометрические фигуры, обладающие центральной симметрией

Задачи Имеют ли центр симметрии: Отрезок Прямая Луч

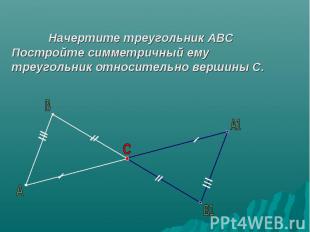
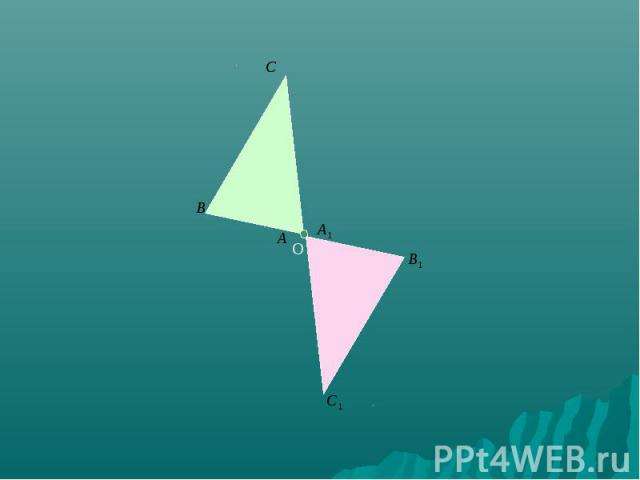
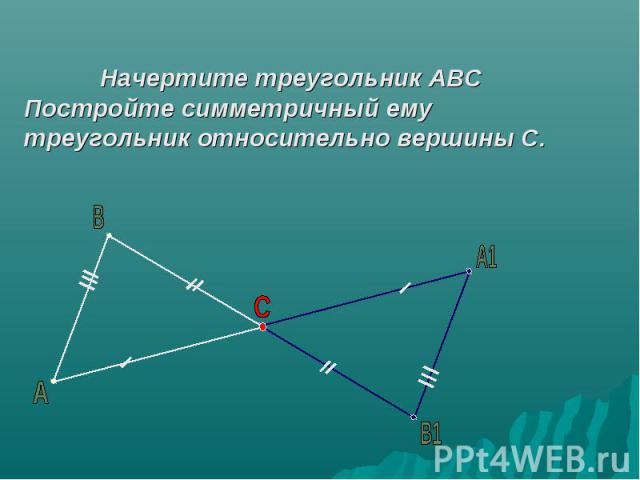
Начертите треугольник АВС Постройте симметричный ему треугольник относительно вершины С.

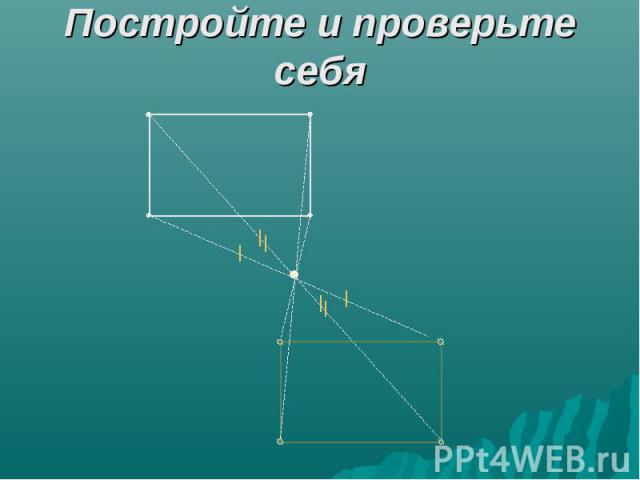
Постройте и проверьте себя

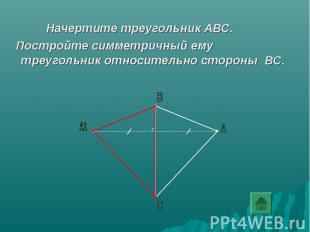
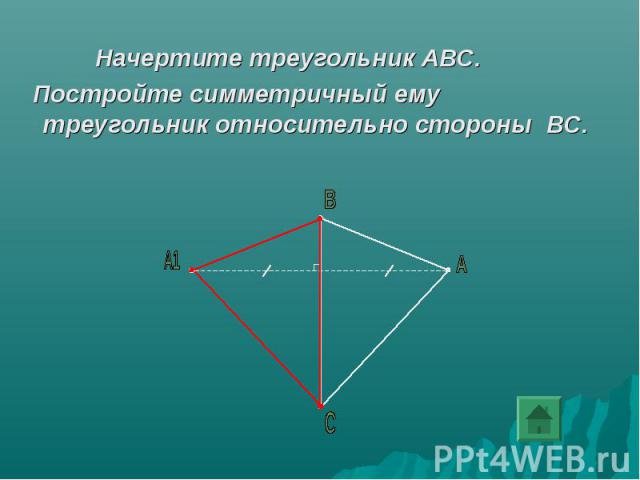
Начертите треугольник АВС. Постройте симметричный ему треугольник относительно стороны ВС.

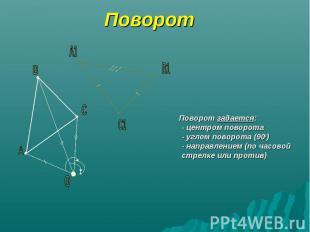
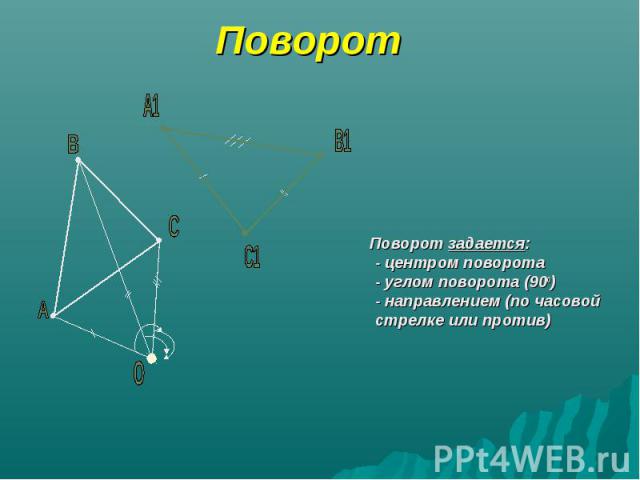
Поворот Поворот задается: - центром поворота - углом поворота (90о) - направлением (по часовой стрелке или против)

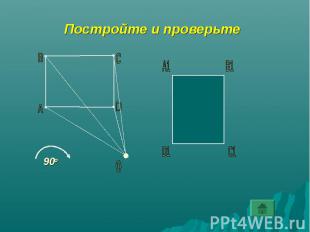
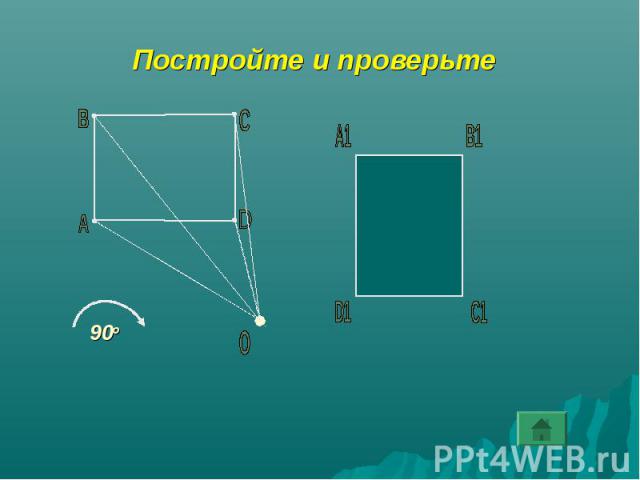
Постройте и проверьте

Симметрия в балете Знаменитые фуэте, когда балерина вращается на одной ножке 6 раз, 12, …, 32 раза! Их повторяемость рождает эстетический эффект, служащий достойным завершением танца!

Винтовая симметрия Листья располагаются на стволе по винтовой линии, чтобы заслонять друг от друга солнечный свет.

Казанский собор

Антисимметрия – это противоположность симметрии, ее отсутствие.

Диссимметрия – это частичное отсутствие симметрии, её расстройство, выраженное в наличии одних симметричных свойств и отсутствии других.

Итог урока С какими новыми понятиями познакомились? Что нового узнали о геометрических фигурах? Приведите примеры геометрических фигур, обладающих осевой симметрией. Приведите пример фигур, обладающих центральной симметрией. Приведите примеры предметов из окружающей жизни, обладающих одной или двумя видами симметрии.

Спасибо за внимание!