Презентация на тему: Геометрия 11 класс

Геометрия 11 класс

1.Как можно получить цилиндр Если в одной из 2 параллельных плоскостей взять окружность, и из каждой ее точки восстановить перпендикуляр до пересечения со второй плоскостью, то получится тело, ограниченное двумя кругами и поверхностью, образованной из перпендикуляров, это тело называется цилиндром. Круги, лежащие в параллельных плоскостях, называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей оснований –называются образующими цилиндра.

А можно так получить цилиндр Вращением прямоугольника вокруг одной из его сторон

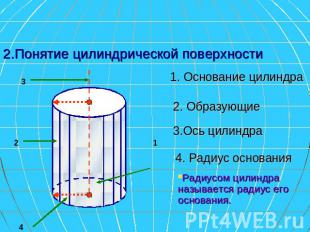
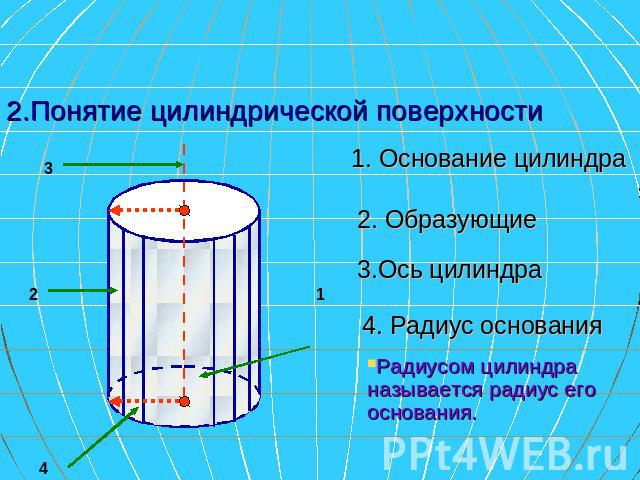
2.Понятие цилиндрической поверхности 1. Основание цилиндра 2. Образующие 3.Ось цилиндра 4. Радиус основания Радиусом цилиндра называется радиус его основания.

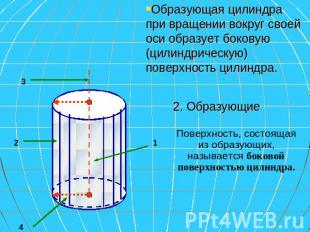
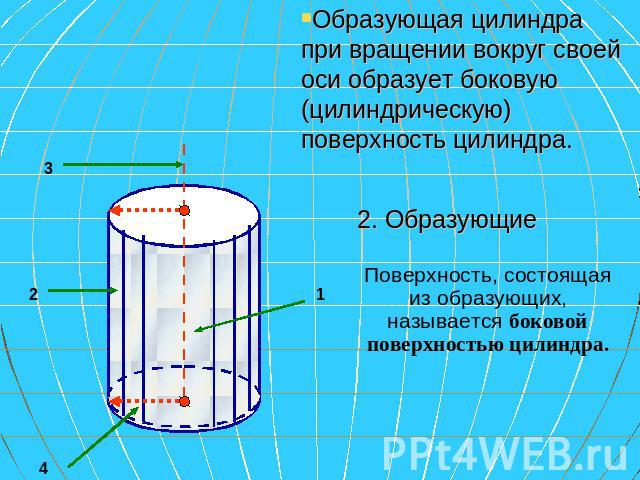
Образующая цилиндра при вращении вокруг своей оси образует боковую (цилиндрическую) поверхность цилиндра. 2. Образующие Поверхность, состоящая из образующих, называется боковой поверхностью цилиндра.

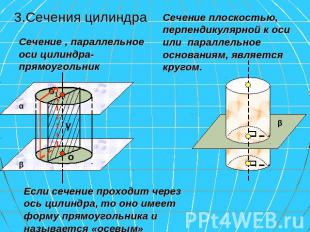
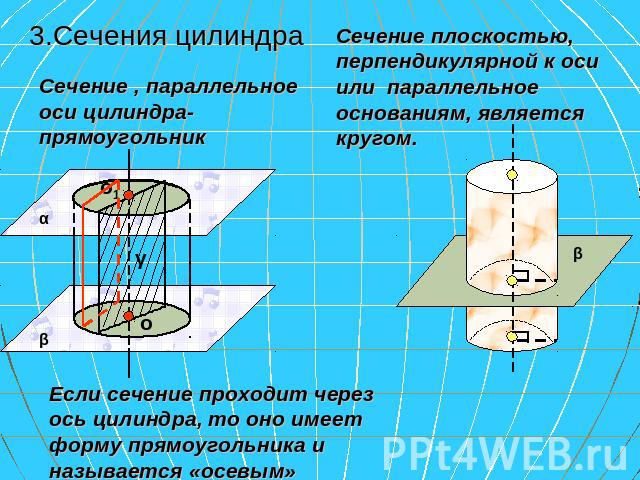
3.Сечения цилиндра Сечение , параллельное оси цилиндра-прямоугольник Сечение плоскостью, перпендикулярной к оси или параллельное основаниям, является кругом. Если сечение проходит через ось цилиндра, то оно имеет форму прямоугольника и называется «осевым»

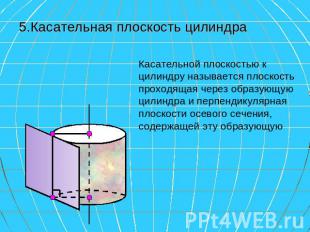
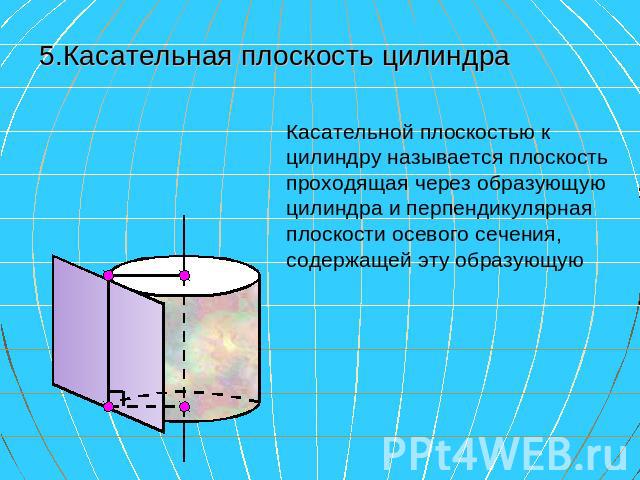
5.Касательная плоскость цилиндра Касательной плоскостью к цилиндру называется плоскость проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую

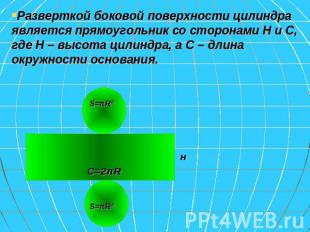
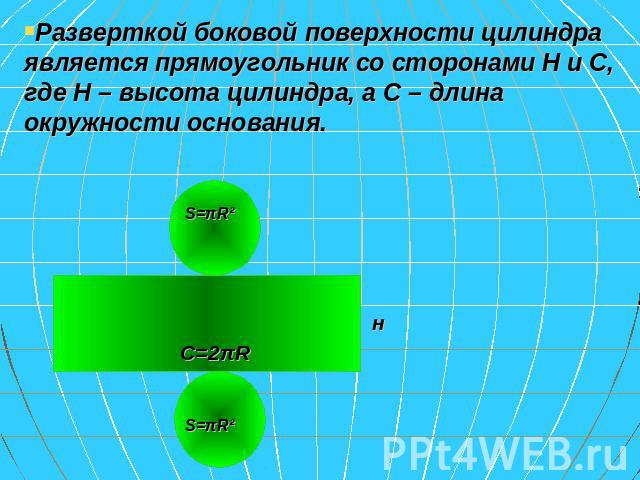
Разверткой боковой поверхности цилиндра является прямоугольник со сторонами Н и С, где Н – высота цилиндра, а С – длина окружности основания.

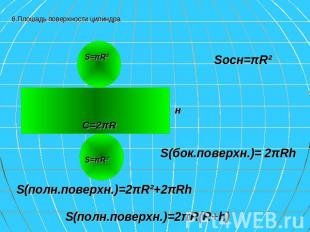
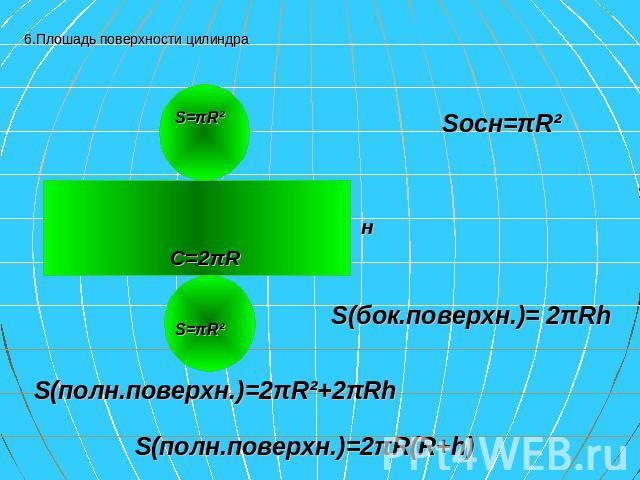
6.Плошадь поверхности цилиндра Sосн=πR² S(бок.поверхн.)= 2πRh S(полн.поверхн.)=2πR²+2πRh S(полн.поверхн.)=2πR(R+h)

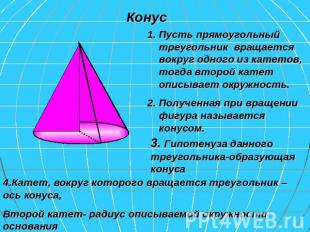
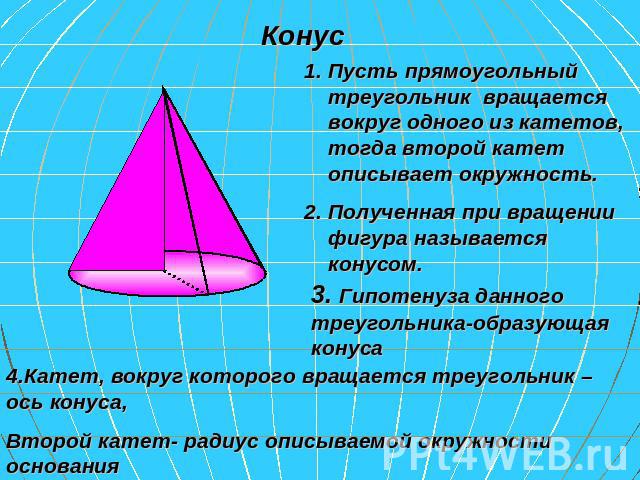
Конус Пусть прямоугольный треугольник вращается вокруг одного из катетов, тогда второй катет описывает окружность. Полученная при вращении фигура называется конусом. 3. Гипотенуза данного треугольника-образующая конуса 4.Катет, вокруг которого вращается треугольник – ось конуса, Второй катет- радиус описываемой окружности основания

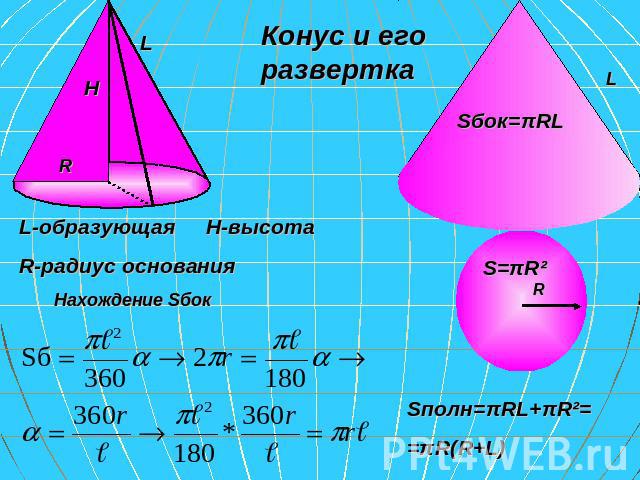
Конус и его развертка

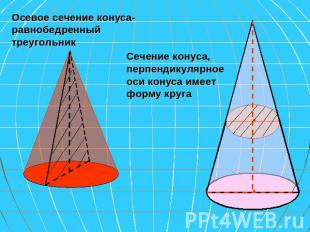
Осевое сечение конуса-равнобедренный треугольник Сечение конуса, перпендикулярное оси конуса имеет форму круга

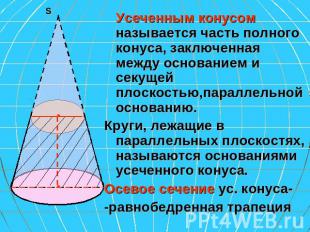
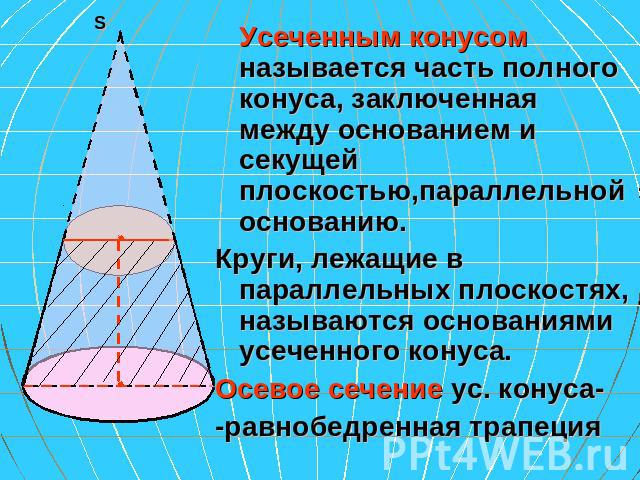
Усеченным конусом называется часть полного конуса, заключенная между основанием и секущей плоскостью,параллельной основанию. Круги, лежащие в параллельных плоскостях, называются основаниями усеченного конуса. Осевое сечение ус. конуса- -равнобедренная трапеция

Образующей усеченного конуса называется часть образующей полного конуса, заключенная между основаниями. Высотой усеченного конуса называется расстояние между основаниями. Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.

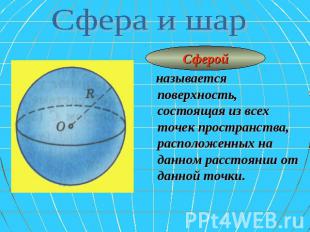
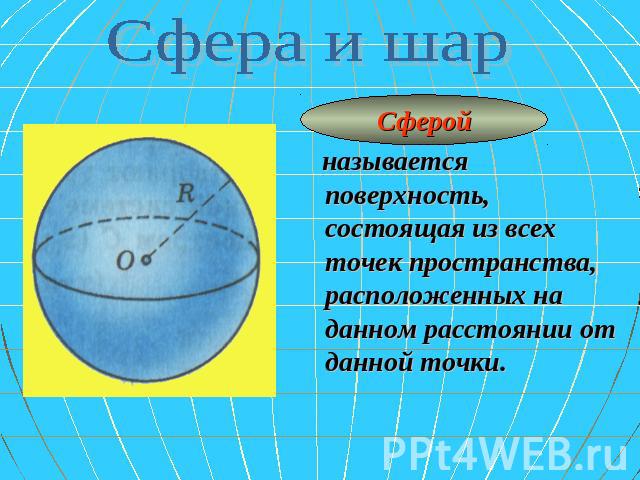
Сфера и шар Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

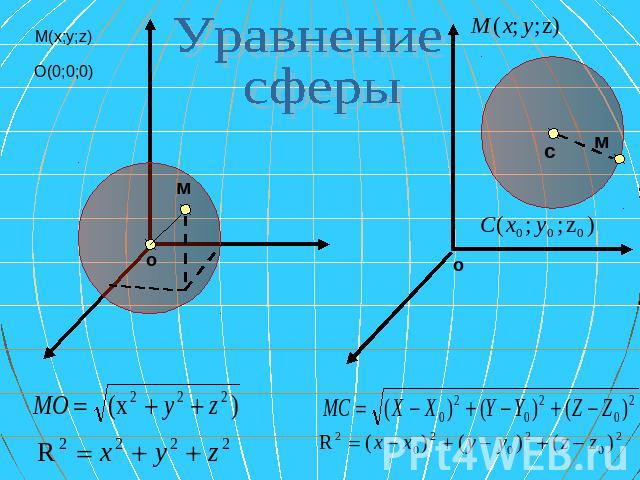
Уравнение сферы

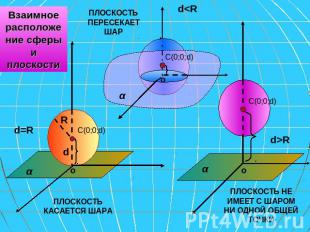
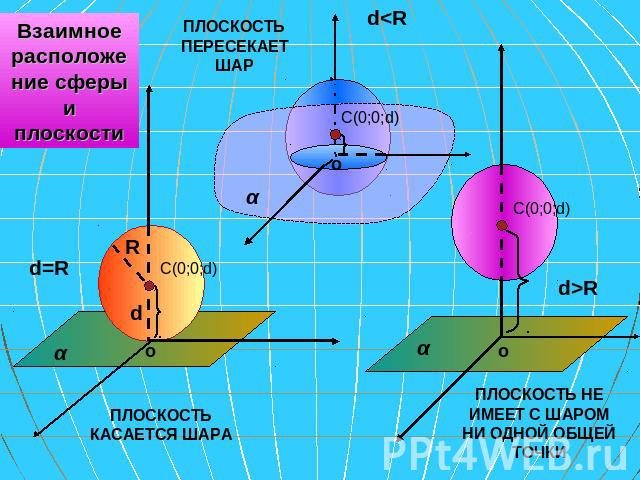
Взаимное расположение сферы и плоскости

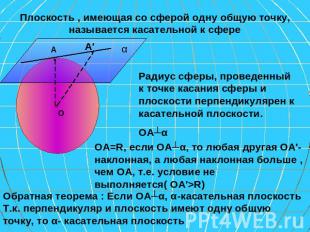
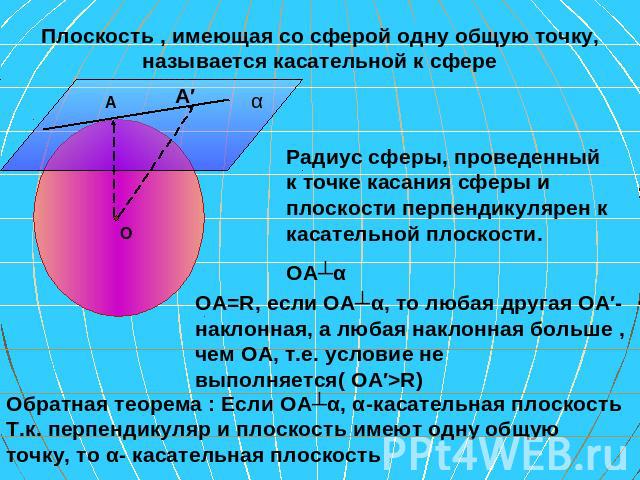
Плоскость , имеющая со сферой одну общую точку, называется касательной к сфере Радиус сферы, проведенный к точке касания сферы и плоскости перпендикулярен к касательной плоскости. ОА┴α ОА=R, если ОА┴α, то любая другая ОА′- наклонная, а любая наклонная больше , чем ОА, т.е. условие не выполняется( ОА′>R) Т.к. перпендикуляр и плоскость имеют одну общую точку, то α- касательная плоскость

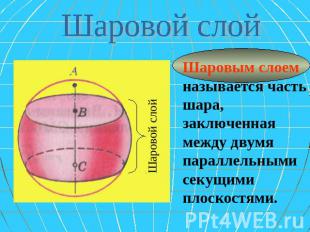
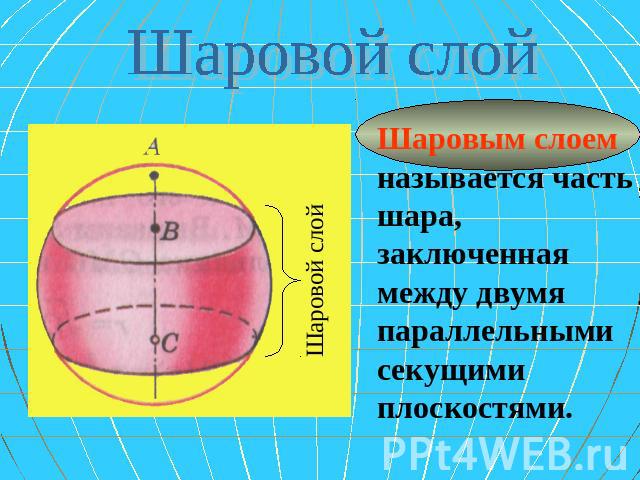
Шаровой слой Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями.

Шаровой сегмент Шаровым сегментом называется часть шара, отсекаемая от него какой - нибудь плоскостью.

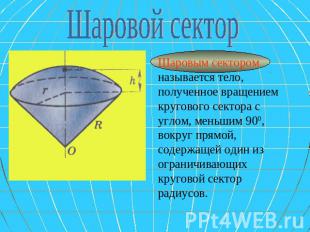
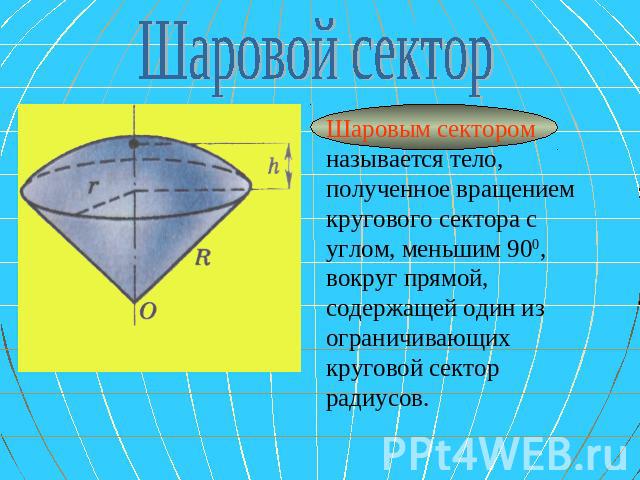
Шаровой сектор Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим 900, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.