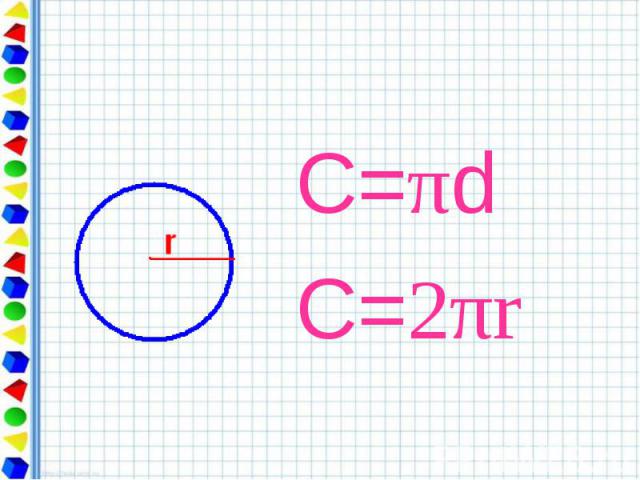Презентация на тему: Длина окружности

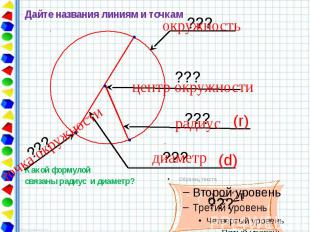
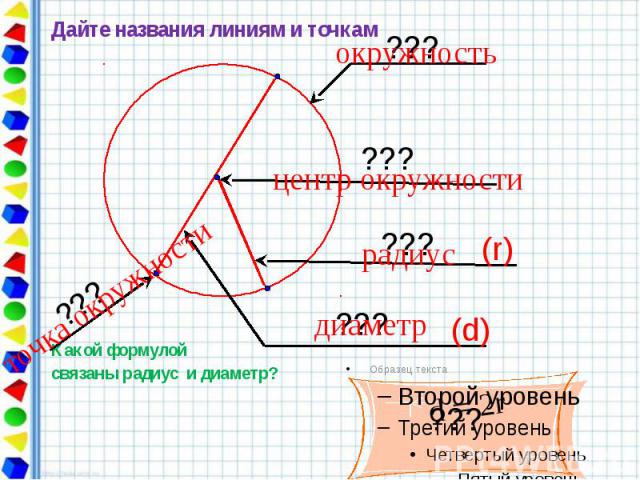
Дайте названия линиям и точкам Дайте названия линиям и точкам Какой формулой связаны радиус и диаметр?

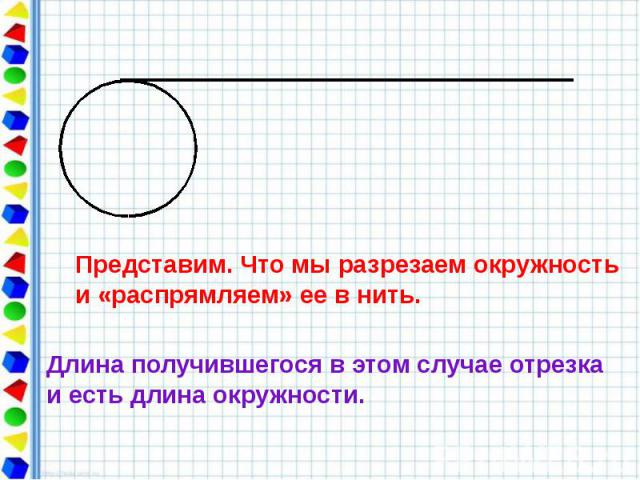
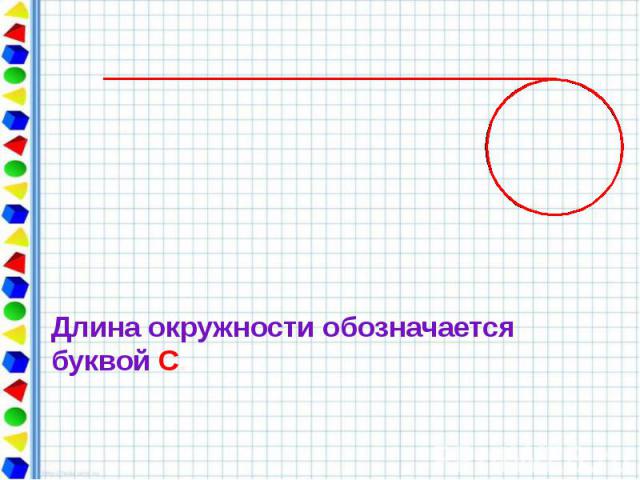
Длину отрезка можно измерить с помощью линейки, длину ломаной можно найти, измерив её звенья и сложив их длины. С помощью специального прибора для измерения длин кривых линий – курвиметра можно измерить и длину окружности. А как вы думаете: каким образом измерить длину окружности без этого прибора?

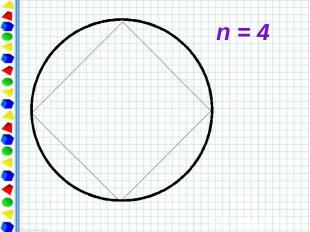
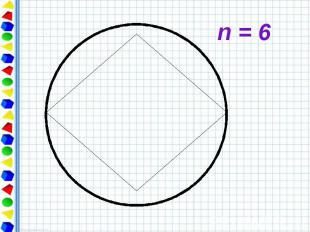
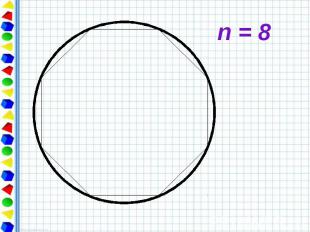
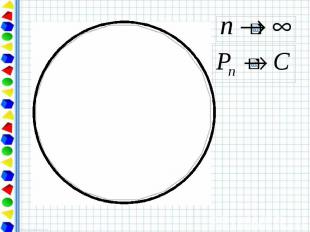
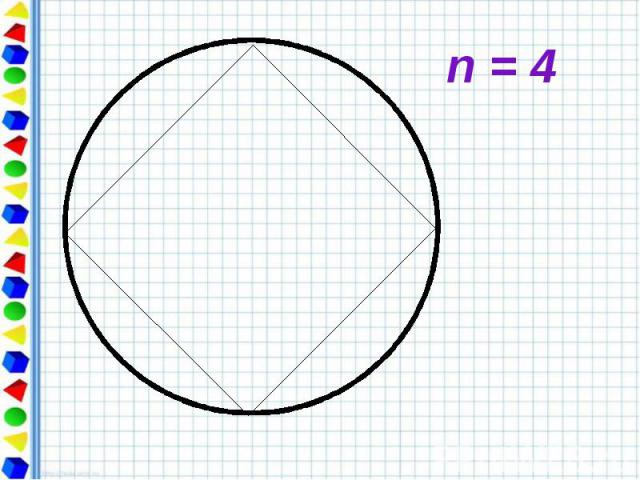
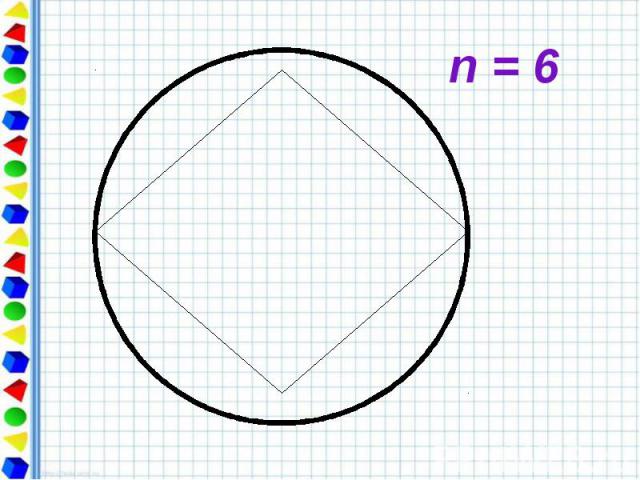
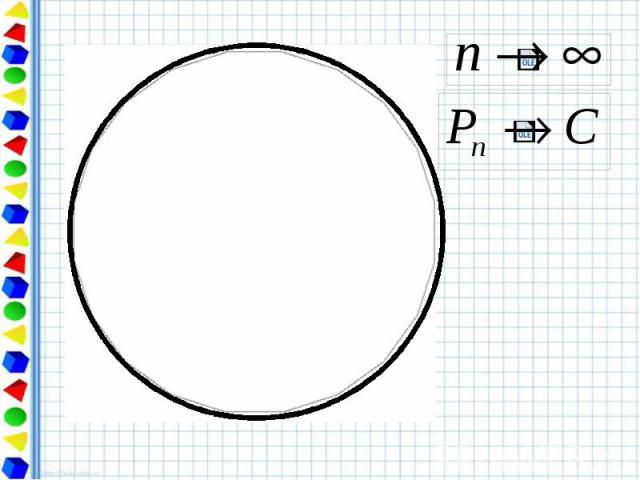
Периметр любого вписанного в окружность многоугольника является приближённым значением длины окружности. При увеличении числа сторон правильный многоугольник всё ближе и ближе «прилегает» к окружности.

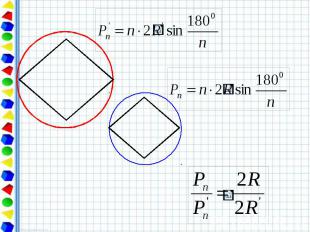
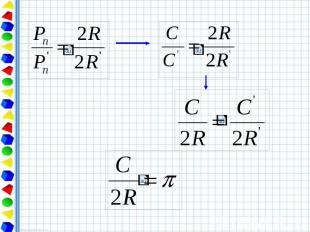
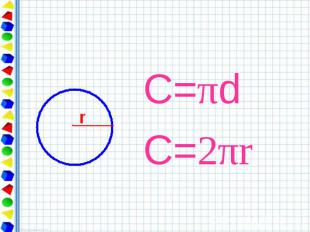
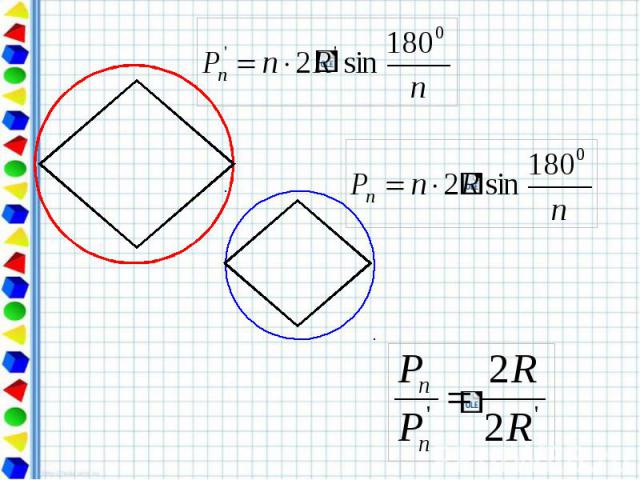
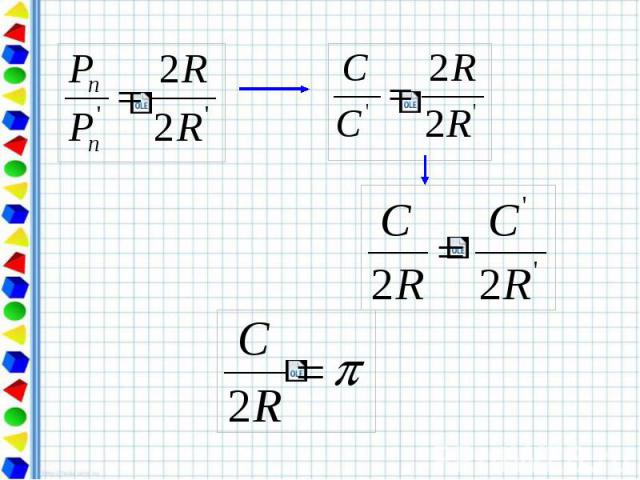
Свойство длины окружности. Отношение длины окружности к её диаметру есть одно и то же число для всех окружностей.

Из древнеегипетских и вавилонских источников известно, что потребности того времени вполне удовлетворяло число, равное трем. Позже римляне принимали равное 3,12. Из древнеегипетских и вавилонских источников известно, что потребности того времени вполне удовлетворяло число, равное трем. Позже римляне принимали равное 3,12. В Древнем Египте считали равным 256/81=3,1604… В истории математики известно, что первое вычисление на основе строгих теоретических рассуждений было выполнено выдающимся математиком древности Архимедом. Архимед (ок.287-212 г.г. до н.э.) жил в г. Сиракузы на о. Сицилия. Погиб от рук римского воина. Перед гибелью Архимед сказал воину: «Не тронь мои круги!». В своем труде «Об измерении круга» он доказал, что находится между числами и , т.е. 3,1408 < <3,1429. Идеи Архимеда почти на два тысячелетия опередили свое время. Значение числа , вычисленное им, многие годы удовлетворяло практическим расчетам людей.

Вычислением числа занимались в более поздние века многие знаменитые математики. Вычислением числа занимались в более поздние века многие знаменитые математики. Французский математик Франсуа Виет вычислил в 1579 году с 9 знаками. Голландский математик Лудольф Ван Цейлен в 1596 г. публикует результат своего десятилетнего труда – число , вычисленное с 32 знаками. Леонард Эйлер (1707-1783) – ученый необычайной широты интересов и творческой продуктивности, автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки. Именно он в 1736 г ввел число для отношения длины окружности к длине ее диаметра. Постепенно увеличивая точность значений, в течение XVIII-XX веков нашли его значение с огромной точностью до 808 десятичных знаков.

Теперь известно, что число иррациональное, может быть представлено в виде бесконечной непериодической десятичной дроби. Теперь известно, что число иррациональное, может быть представлено в виде бесконечной непериодической десятичной дроби. С помощью компьютера число вычислено с точностью до миллиона знаков, но это представляет скорее технический, чем научный интерес…

Задачи по теме «Длина окружности»

Теоретические сведения

Задача: 1) вычислить длину окружности, если ее диаметр равен 6 см 2) вычислить длину окружности, если ее радиус равен 4 см

Решение: 1) D=6 см С= 3,14• 6 =18,84 (см) Ответ: длина окружности 18,84 см

Задача: Длина окружности цирковой арены равна 41 м. Найдите диаметр арены цирка

Решение:

С = 3,14•5=15,7 (м) Ответ: длина полосы дерна равна 15,7 м

Решите задачу

Решение

Отлитый в 1735 г. Царь колокол, хранящийся в Московском Кремле, имеет диаметр основания 6,6 м. Вычислите длину окружности основания Царь-колокола. Диаметр колеса обозрения «Глаз Лондона» равен 135 м (рис. 96). Какой путь делает каждая из его гондол за один оборот вокруг центра колеса? (Кстати, лондонское колесо обозрения самое большое в Европе. А слово «гондола» означает «кабина», а вообще гондолами называют особые лодки, в которых передвигаются жители Венеции по их улицам-рекам).

Решите задачу

Решите задачу

Решите задачу

Задача (О Тунгусском метеорите, 1908 г.) Диаметр опалённой площади тайги от взрыва Тунгусского метеорита равен примерно 38 км. Какова длина полосы тайги, которая пострадала от метеорита?

Древнегреческий математик Архимед установил, что длина окружности относится к длине диаметра приближенно как 22:7. Найдите длину окружности, диаметр которой 4,2 дм.

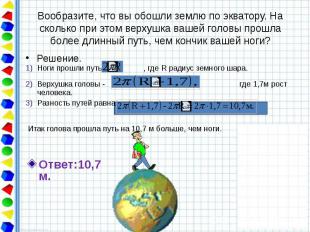
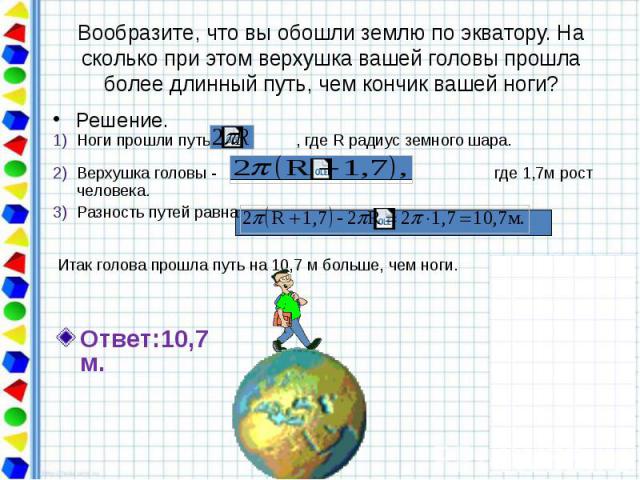
Вообразите, что вы обошли землю по экватору. На сколько при этом верхушка вашей головы прошла более длинный путь, чем кончик вашей ноги? Решение.

Если обтянуть земной шар по экватору проволокой и затем прибавить к её длине 1м, то сможет ли между проволокой и землёй проскочить мышь. Решение. Пусть длина промежутка х см.

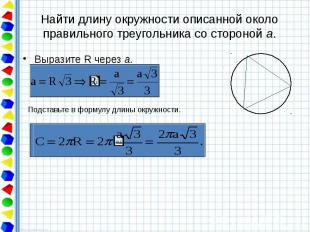
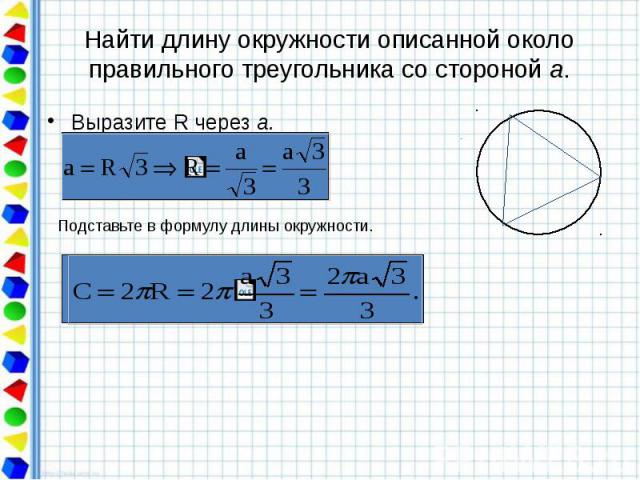
Найти длину окружности описанной около правильного треугольника со стороной а. Выразите R через а.

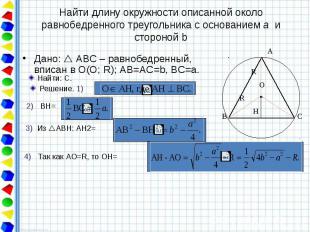
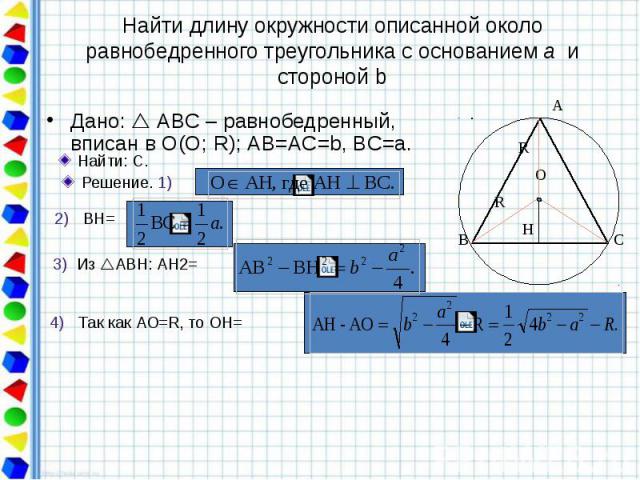
Найти длину окружности описанной около равнобедренного треугольника с основанием а и стороной b Дано: АВС – равнобедренный, вписан в О(О; R); АВ=AС=b, BC=a.

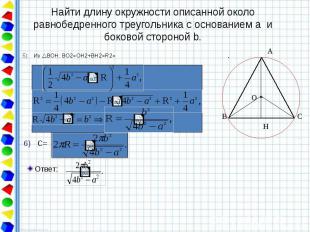
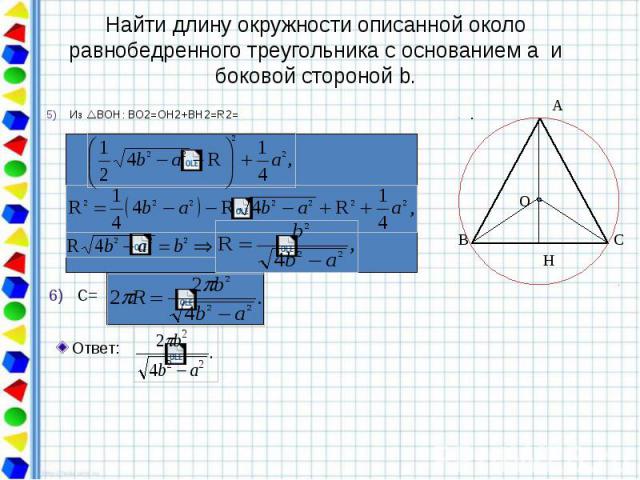
Найти длину окружности описанной около равнобедренного треугольника с основанием a и боковой стороной b. Из ВОН: BО2=OH2+BH2=R2=

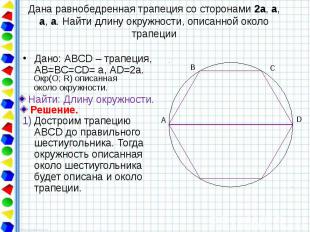
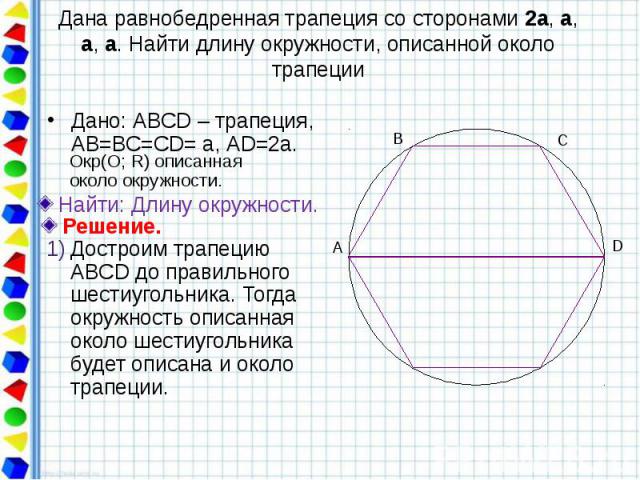
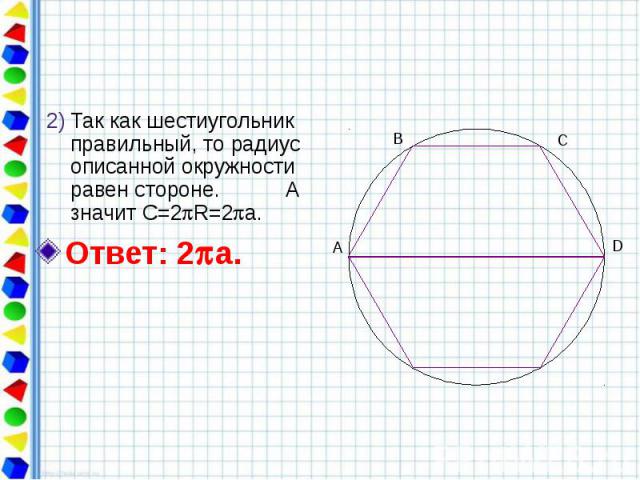
Дана равнобедренная трапеция со сторонами 2a, a, a, a. Найти длину окружности, описанной около трапеции Дано: АВСD – трапеция, АВ=ВС=СD= а, АD=2а.

Интересные факты Отношение длины основания Великой Пирамиды к ее высоте, разделенное пополам, дает знаменитое число "пи" . Возможно, оно намеренно зашифровано в размерах Пирамиды Хеопса, причем с более точным значением, чем его знал великий Архимед, живший позже на 2000 лет!

Интересные факты Лидером по тупым законам по праву может считаться Американский штат Индиана. Там на ряду с законами запрещающими носить усы людям часто прибегающим к поцелуям, продавать молоко в винных магазинах и перекрашивать в другой цвет птиц и животных, действует закон о том, что на территории штата число . следует считать равным 4