Презентация на тему: «Длина окружности»

Понятие длины окружности. Представим себе нить в форме окружности. Разрежем её и растянем за концы.

Периметр любого вписанного в окружность многоугольника является приближённым значением длины окружности. При увеличении числа сторон правильный многоугольник всё ближе и ближе «прилегает» к окружности.

Свойство длины окружности. Отношение длины окружности к её диаметру есть одно и то же число для всех окружностей. ( стр. 265, курсив предпоследний абзац)

Доказательство: 1) Впишем в каждую окружность правильный n-угольник.

Число «пи». Вывод формулы длины окружности. Из свойства длины окружности следует . что есть число постоянное и теоретически доказано, что это число иррациональное. Обозначают его греческой буквой «пи».

Задача 1. Вообразите, что вы обошли землю по экватору. На сколько при этом верхушка вашей головы прошла более длинный путь, чем кончик вашей ноги? Решение.

Задача 2. Если обтянуть земной шар по экватору проволокой и затем прибавить к её длине 1м, то сможет ли между проволокой и землёй проскочить мышь. Решение. Пусть длина промежутка х см.

№ 1104(а). Найти длину окружности описанной около правильного треугольника со стороной а. Выразите R через а.

№ 1104 (в). Найти длину окружности описанной около равнобедренного треугольника с основанием а и Дано: АВС – равнобедренный, вписан в О(О; R); АВ=AС=b, BC=a.

№ 1104 (в). Найти длину окружности описанной около равнобедренного треугольника с основанием Из ВОН: BО2=OH2+BH2=R2=

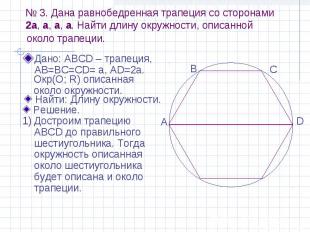
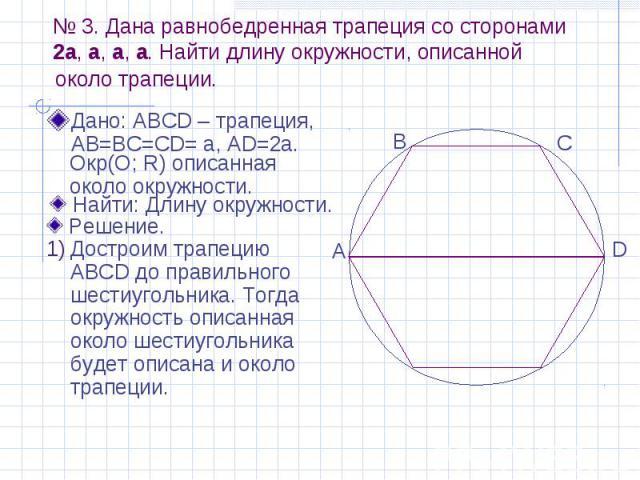
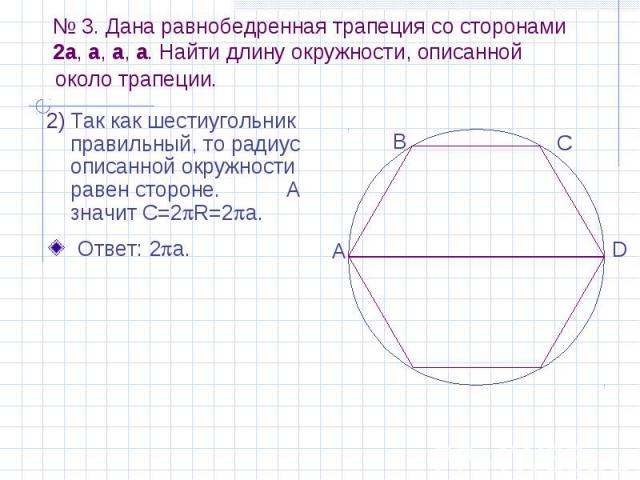
№ 3. Дана равнобедренная трапеция со сторонами 2a, a, a, a. Найти длину окружности, описанной Дано: АВСD – трапеция, АВ=ВС=СD= а, АD=2а.

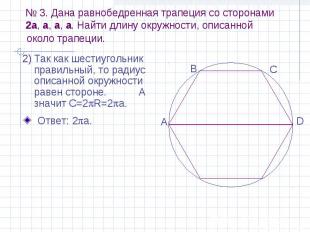
№ 3. Дана равнобедренная трапеция со сторонами 2a, a, a, a. Найти длину окружности, описанной

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ Сформулируйте основное свойство длины окружности. На чём основывается его доказательство?

Домашнее задание     Вопросы 8-9(стр. 270).     №1108, №1105(а).

Спасибо за урок, дети.