Презентация на тему: Перпендикуляр и наклонная

Перпендикуляр и наклонная Свойство биссектрисы углаГеометрическое место точекЗадачи

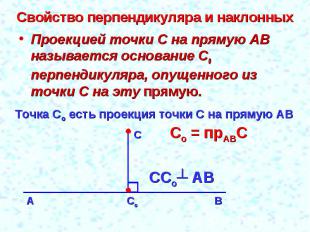
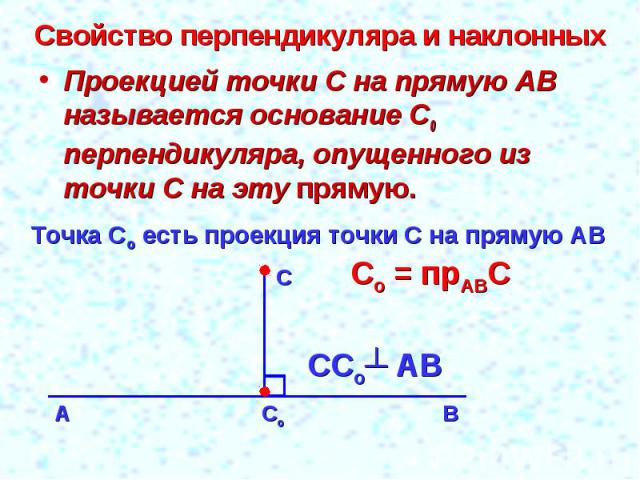
Свойство перпендикуляра и наклонных Проекцией точки С на прямую АВ называется основание С0 перпендикуляра, опущенного из точки С на эту прямую.Точка Со есть проекция точки С на прямую АВСо = прАВС

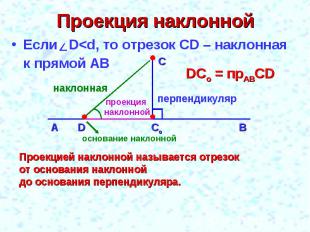
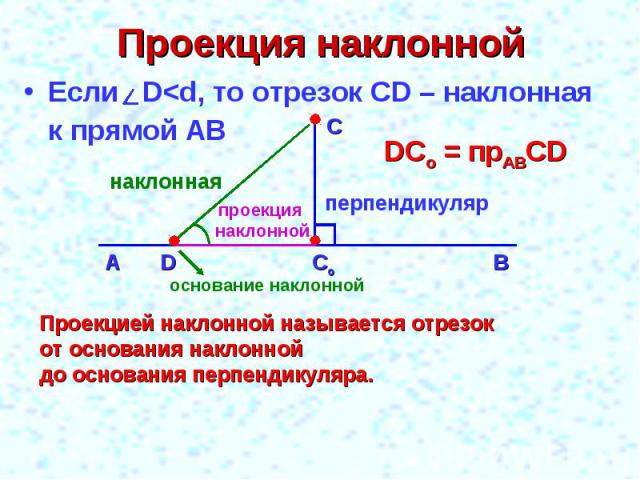
Проекция наклонной Если D<d, то отрезок CD – наклонная к прямой АВ Проекцией наклонной называется отрезок от основания наклонной до основания перпендикуляра.

Теоремы о перпендикуляре и наклонной т.1 Если из точки проведены к прямой наклонная и перпендикуляр, то перпендикуляр короче (меньше) наклонной.Дано: ССо┴АВСD – наклоннаяДок-ть: ССо<CDДок-во:ΔDCCo – прямоугольный, Со=90о, т.к. ССо┴АВ по усл. ССо – катет, СD – гипотенуза ССо<CD, ч.т.д.

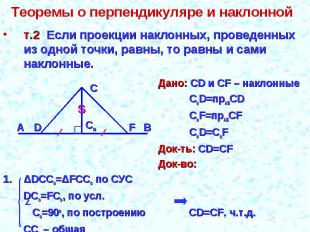
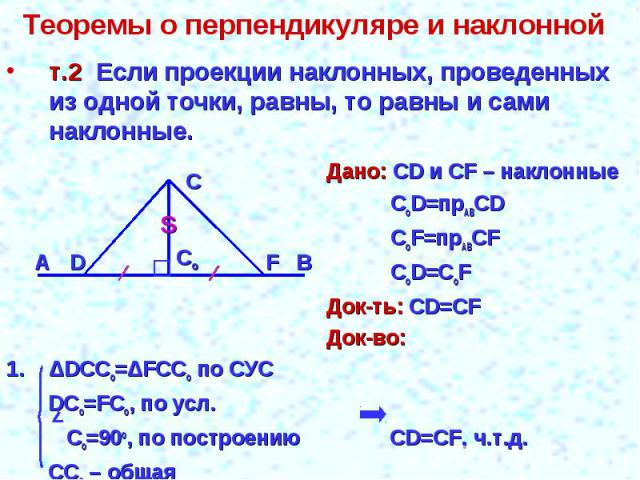
Теоремы о перпендикуляре и наклонной т.2 Если проекции наклонных, проведенных из одной точки, равны, то равны и сами наклонные.Дано: СD и СF – наклонныеCoD=прABСDCoF=прABСFCoD=СоFДок-ть: СD=CFДок-во:ΔDCCo=ΔFCCo по СУС DCo=FCo, по усл. Co=90o, по построению CD=CF, ч.т.д. CCo – общая

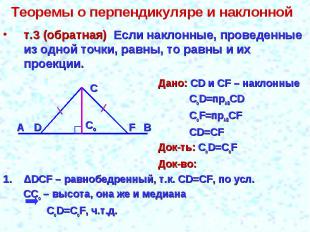
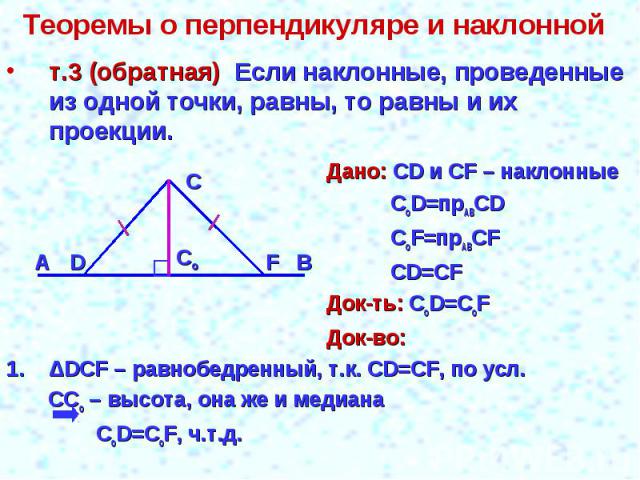
Теоремы о перпендикуляре и наклонной т.3 (обратная) Если наклонные, проведенные из одной точки, равны, то равны и их проекции.Дано: СD и СF – наклонныеCoD=прABСDCoF=прABСFCD=СFДок-ть: СоD=CоFДок-во:ΔDCF – равнобедренный, т.к. CD=CF, по усл. CCо – высота, она же и медиана CоD=CоF, ч.т.д.

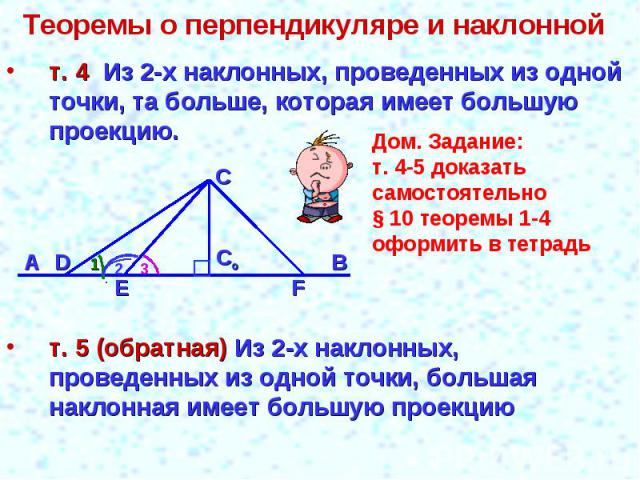
Теоремы о перпендикуляре и наклонной т. 4 Из 2-х наклонных, проведенных из одной точки, та больше, которая имеет большую проекцию.Дом. Задание:т. 4-5 доказать самостоятельно§ 10 теоремы 1-4оформить в тетрадьт. 5 (обратная) Из 2-х наклонных, проведенных из одной точки, большая наклонная имеет большую проекцию

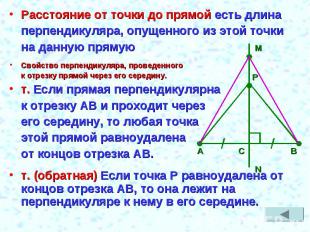
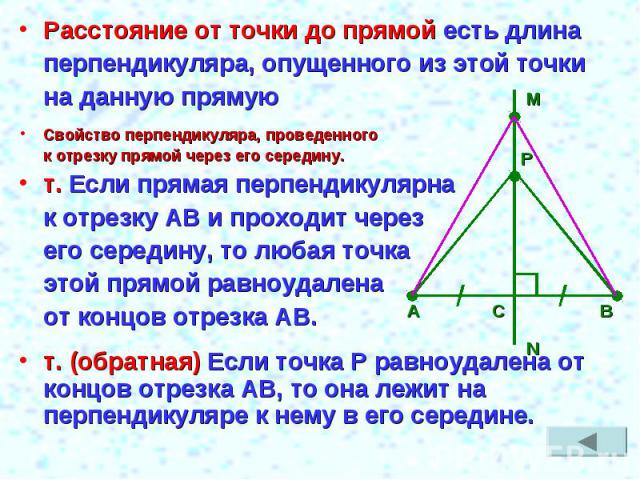
Расстояние от точки до прямой есть длинаперпендикуляра, опущенного из этой точкина данную прямуюСвойство перпендикуляра, проведенного к отрезку прямой через его середину.т. Если прямая перпендикулярна к отрезку АВ и проходит через его середину, то любая точка этой прямой равноудалена от концов отрезка АВ.т. (обратная) Если точка Р равноудалена от концов отрезка АВ, то она лежит на перпендикуляре к нему в его середине.

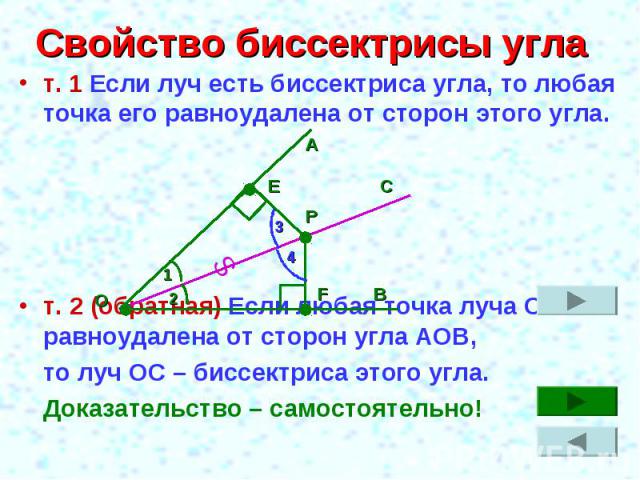
Свойство биссектрисы угла т. 1 Если луч есть биссектриса угла, то любая точка его равноудалена от сторон этого угла.т. 2 (обратная) Если любая точка луча ОС равноудалена от сторон угла АОВ, то луч ОС – биссектриса этого угла.Доказательство – самостоятельно!

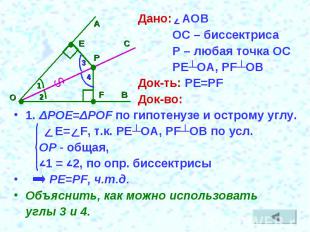
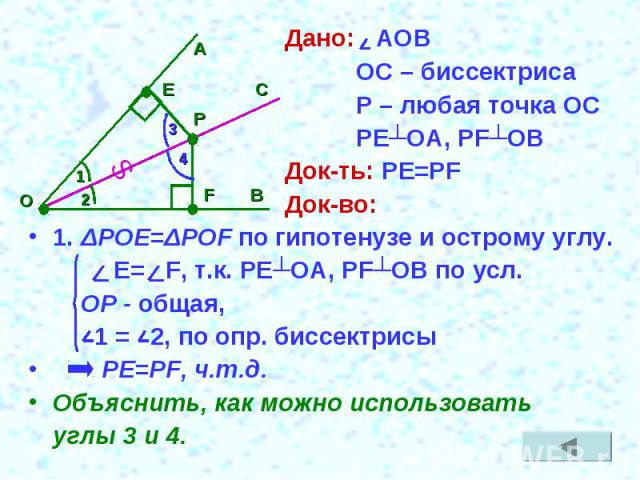
Дано: АОВ ОС – биссектриса Р – любая точка ОС РЕ┴ОА, РF┴ОВДок-ть: PE=PFДок-во:1. ΔРОЕ=ΔPOF по гипотенузе и острому углу. Е= F, т.к. РЕ┴ОА, РF┴ОВ по усл. ОР - общая, 1 = 2, по опр. биссектрисы PE=PF, ч.т.д.Объяснить, как можно использовать углы 3 и 4.

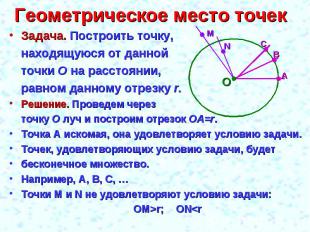
Геометрическое место точек Задача. Построить точку, находящуюся от данной точки О на расстоянии, равном данному отрезку r.Решение. Проведем через точку О луч и построим отрезок ОА=r.Точка А искомая, она удовлетворяет условию задачи.Точек, удовлетворяющих условию задачи, будетбесконечное множество.Например, А, В, С, …Точки М и N не удовлетворяют условию задачи:ОМ>r; ON<r

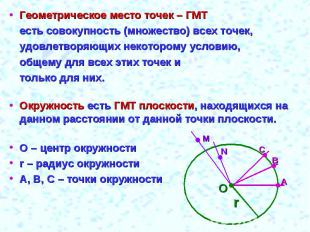
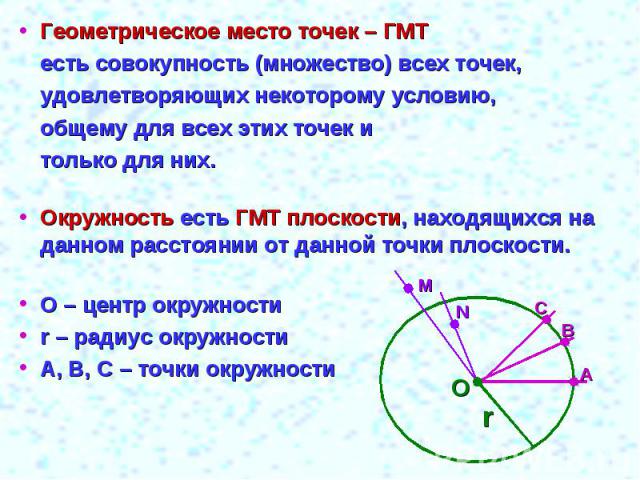
Геометрическое место точек – ГМТесть совокупность (множество) всех точек,удовлетворяющих некоторому условию,общему для всех этих точек итолько для них.Окружность есть ГМТ плоскости, находящихся на данном расстоянии от данной точки плоскости. О – центр окружностиr – радиус окружностиА, В, С – точки окружности

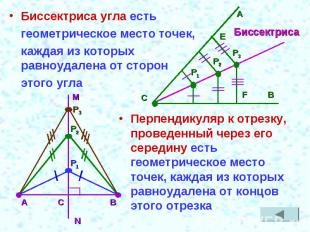
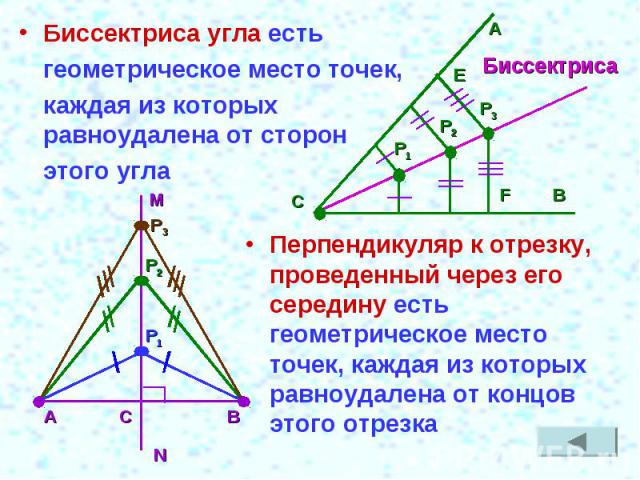
Биссектриса угла есть геометрическое место точек, каждая из которых равноудалена от сторон этого углаПерпендикуляр к отрезку, проведенный через его середину есть геометрическое место точек, каждая из которых равноудалена от концов этого отрезка

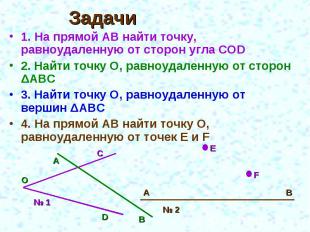
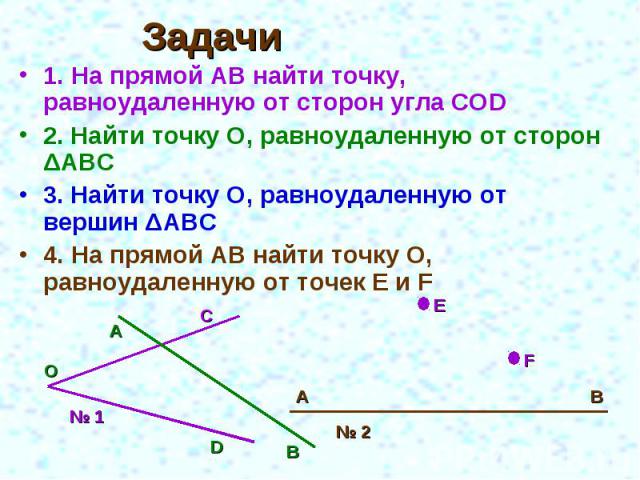
Задачи 1. На прямой АВ найти точку, равноудаленную от сторон угла COD2. Найти точку О, равноудаленную от сторон ΔАВС3. Найти точку О, равноудаленную от вершин ΔАВС4. На прямой АВ найти точку О, равноудаленную от точек E и F

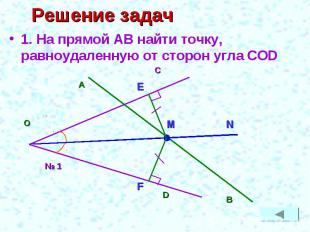
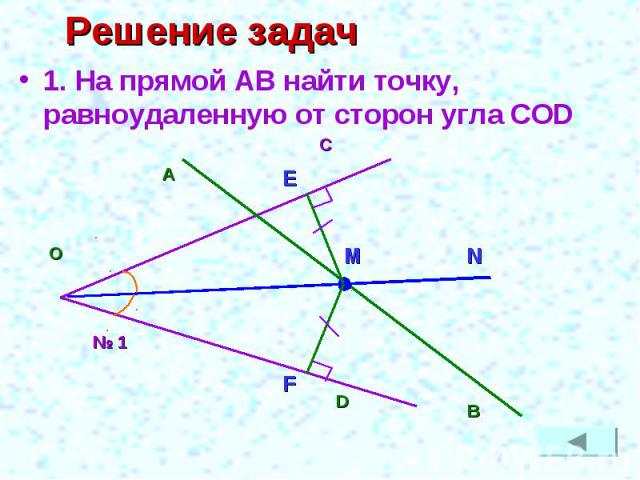
Решение задач 1. На прямой АВ найти точку, равноудаленную от сторон угла COD

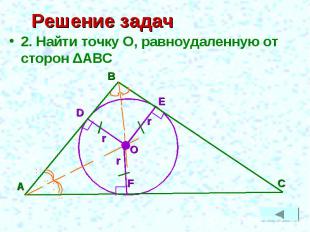
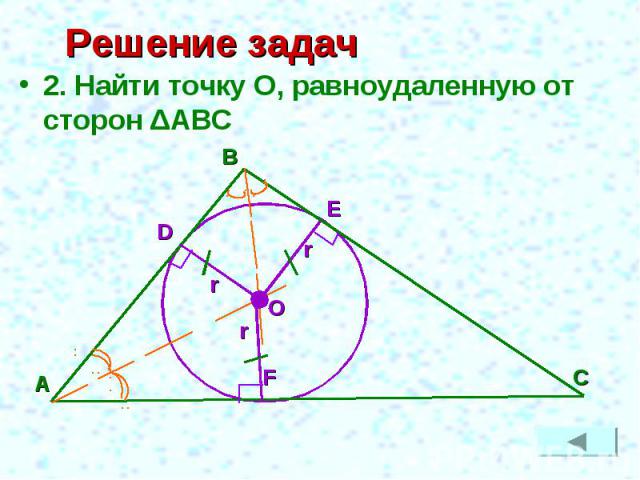
Решение задач 2. Найти точку О, равноудаленную от сторон ΔАВС

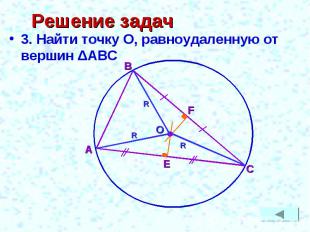
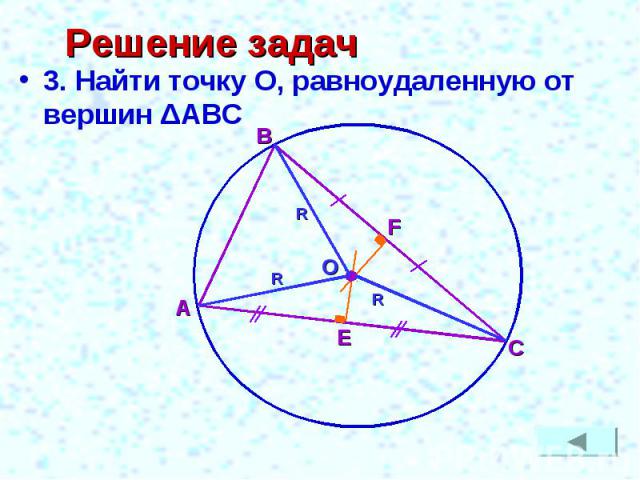
Решение задач 3. Найти точку О, равноудаленную от вершин ΔАВС

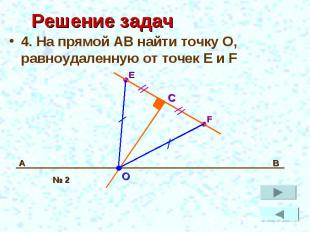
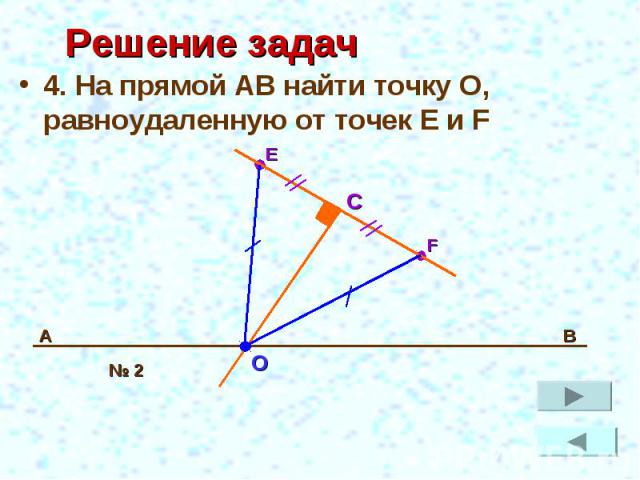
Решение задач 4. На прямой АВ найти точку О, равноудаленную от точек E и F

Спасибо за внимание!