Презентация на тему: Теорема косинусов. Следствия из теоремы косинусов

Теорема косинусов.Следствия из теоремы косинусов.

Проверка домашнего задания.№1Определите вид треугольника заданного своим сторонами 17, 8,15.Решение:Наибольший угол лежит против стороны, равной 17, то по следствию из теоремы косинусов:Треугольник прямоугольный.Ответ: треугольник прямоугольный.№ 2Найдите сторону АВ в треугольнике АВС, если АС=0,6, ВС= , ∠С=150о.Решение :По теореме косинусов:АВ2=0,62 + ( )2 - 2∙ 0, 6∙ ∙ , АВ2=0,9975АВ=Ответ :  

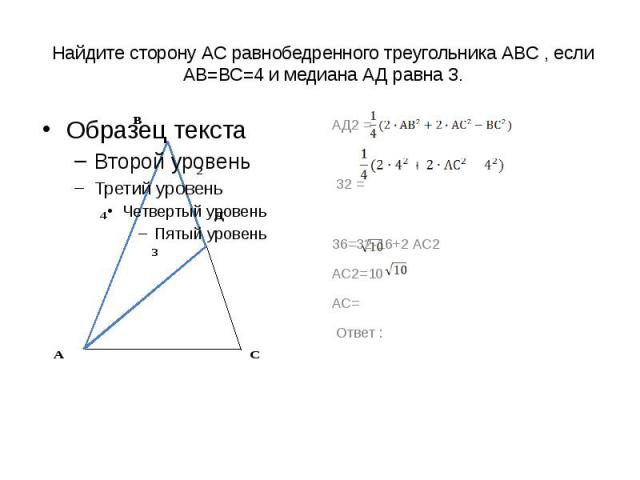
Проверка домашнего задания. №3Найдите сторону АС равнобедренного треугольника АВС , если АВ=ВС=4 и медиана АД равна 3.Решение:∆АВД:Следствие из т. косинусов:∆АВС:Т. косинусов :АС2=42 +42 -2∙4∙4∙ =10АС=Ответ:

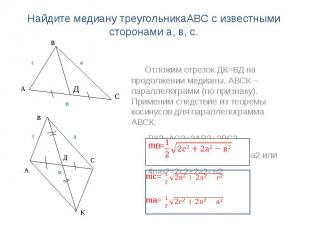
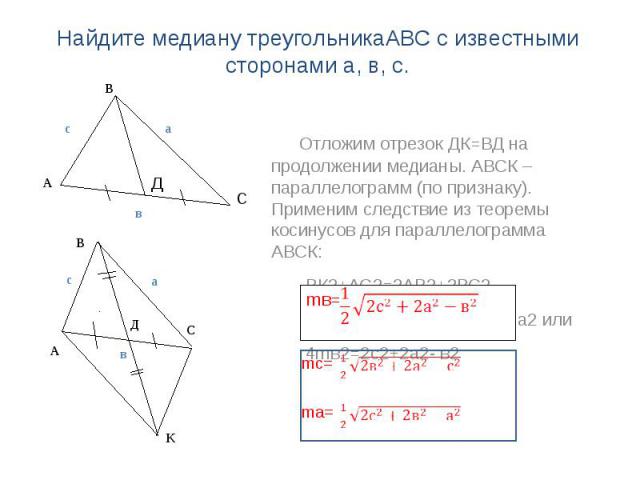
Найдите медиану треугольникаАВС с известными сторонами а, в, с. Отложим отрезок ДК=ВД на продолжении медианы. АВСК – параллелограмм (по признаку). Применим следствие из теоремы косинусов для параллелограмма АВСК: ВК2+АС2=2АВ2+2ВС2 Значит, (2mв)²+ в2=2с2+2а2 или 4mв2=2с2+2а2- в2

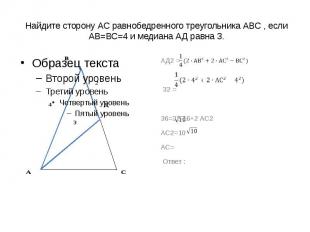
Найдите сторону АС равнобедренного треугольника АВС , если АВ=ВС=4 и медиана АД равна 3. АД2 = 32 =36=32-16+2 АС2АС2=10АС= Ответ :

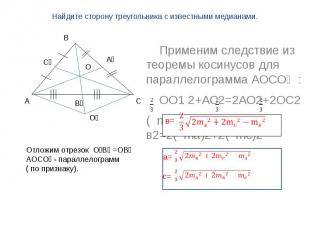
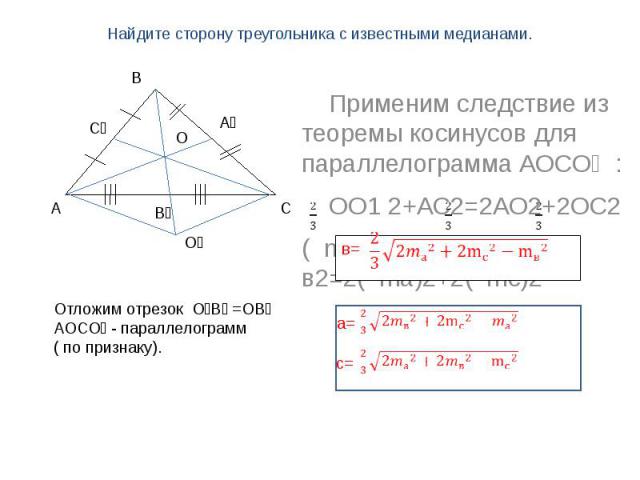
Найдите сторону треугольника с известными медианами. Применим следствие из теоремы косинусов для параллелограмма АОСО₁ : ОО1 2+АС2=2АО2+2ОС2( mв )2 + в2=2( ma)2+2( mс)2 Отложим отрезок О₁В₁ =ОВ₁АОСО₁ - параллелограмм( по признаку).

Сторона треугольника равна 20, а медианы , проведенные к другим сторонам равны 18 и 24 соответственно. Найдите третью медиану треугольника. Дано:АС=20АА₁ и ВВ₁ и СС₁ - медианыАА₁=24СС₁=18Найти: ВВ₁. АС2= 400= (2∙3²6²+2 ) =2∙6²(9+16)-900==2∙30²-900=900ВВ 1=30Ответ: 30.

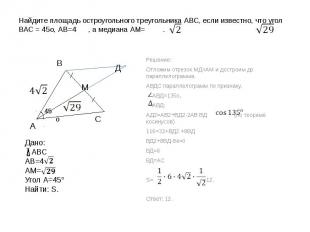
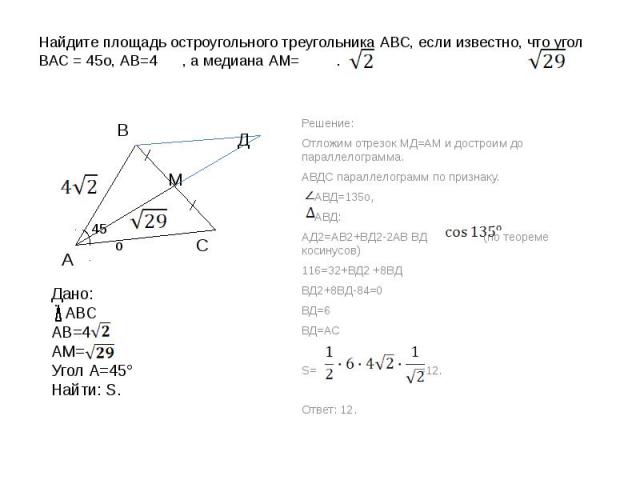
Найдите площадь остроугольного треугольника АВС, если известно, что угол ВАС = 45о, АВ=4 , а медиана АМ= . Дано: АВСАВ=4АМ=Угол А=45°Найти: S. Решение:Отложим отрезок МД=АМ и достроим до параллелограмма.АВДС параллелограмм по признаку. АВД=135о, АВД: АД2=АВ2+ВД2-2АВ ВД (по теореме косинусов)116=32+ВД2 +8ВДВД2+8ВД-84=0ВД=6ВД=АСS= =12.Ответ: 12. 

Домашнее задание. Найдите площадь треугольника, если две стороны его соответственно равны 27 и 29, а медиана проведенная к третьей стороне равна 26.Найдите площадь остроугольного треугольника АВС, если известно, что АВ=6 , а медиана АМ= .Докажите, что

Математика, правильно понятая, обладает не только истинной, но и величайшей красотой.Бертран Рёссель