Презентация на тему: Перпендикуляр и наклонная. Угол между прямой и плоскостью.

Перпендикуляр и наклонная. Угол между прямой и плоскостью
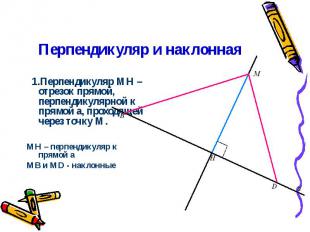
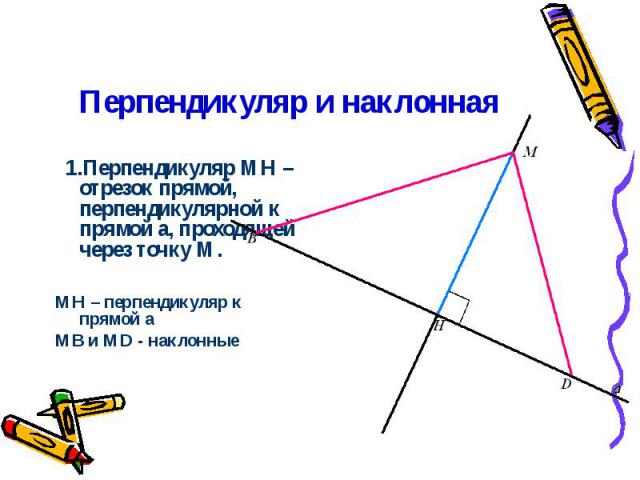
Перпендикуляр и наклонная 1.Перпендикуляр МН – отрезок прямой, перпендикулярной к прямой a, проходящей через точку М. MН – перпендикуляр к прямой a МВ и MD - наклонные
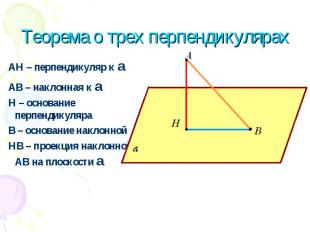
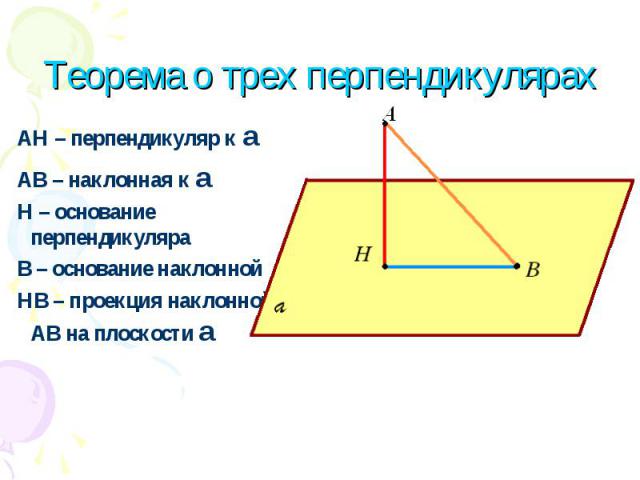
АН – перпендикуляр к a АВ – наклонная к a Н – основание перпендикуляра В – основание наклонной НВ – проекция наклонной АВ на плоскости a Теорема о трех перпендикулярах
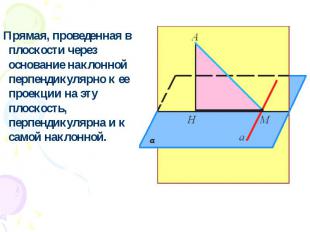
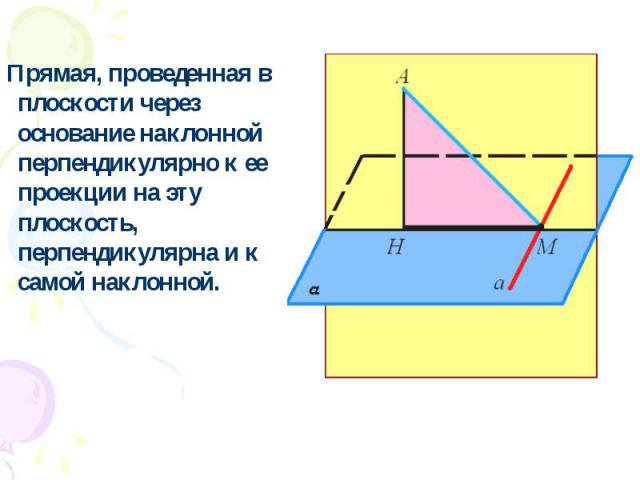
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
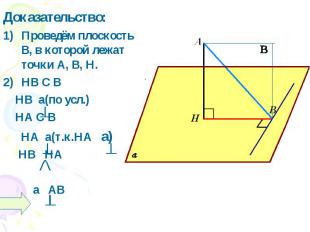
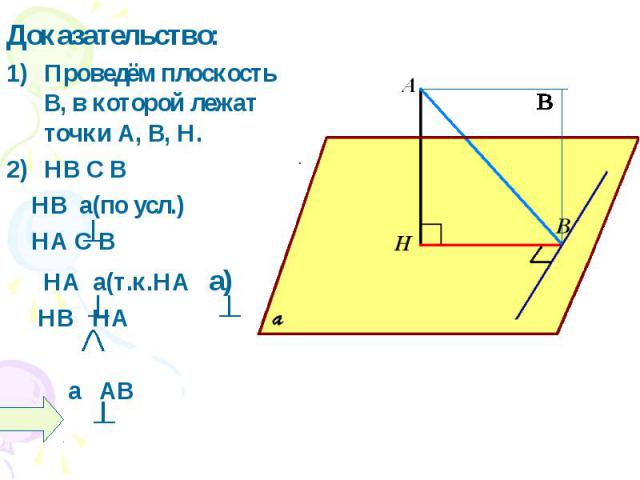
Доказательство: 1)Проведём плоскость B, в которой лежат точки А, В, Н. 2)HB C B HB a(по усл.) НА С B НА a(т.к.НА a ) НВ НА а АВ

Верно и обратное: Прямая, проведённая в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.

Перпендикуляр и наклонная. Угол между прямой и плоскостью
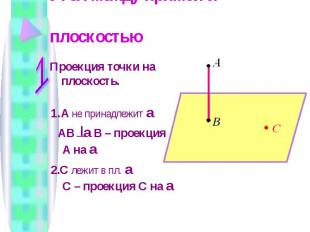
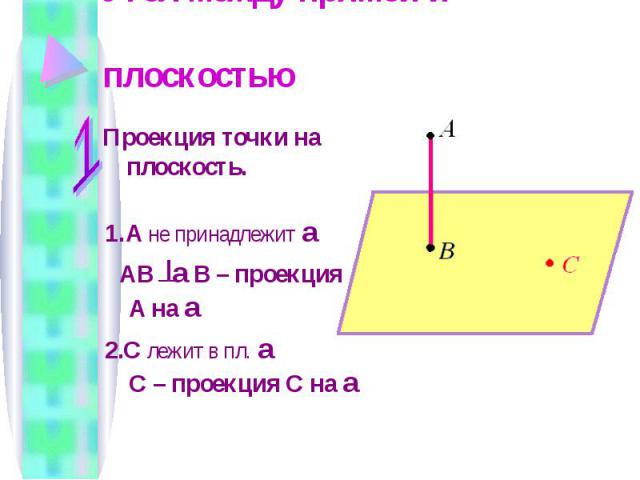
Угол между прямой и плоскостью Проекция точки на плоскость. 1. A не принадлежит a AB a B – проекция A на a 2.С лежит в пл. a С – проекция С на a
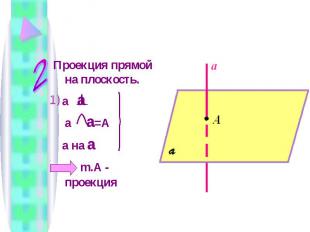
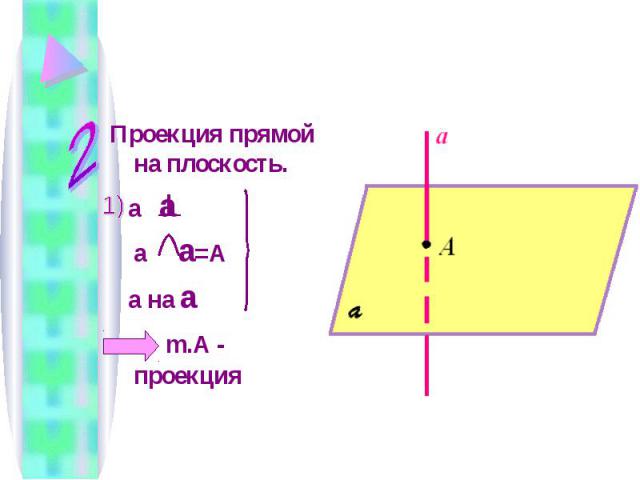
Проекция прямой на плоскость. a a a a =A a на a m.A - проекция
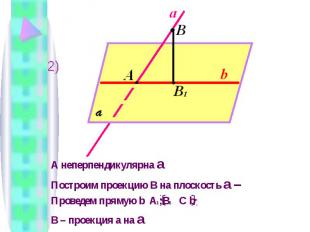
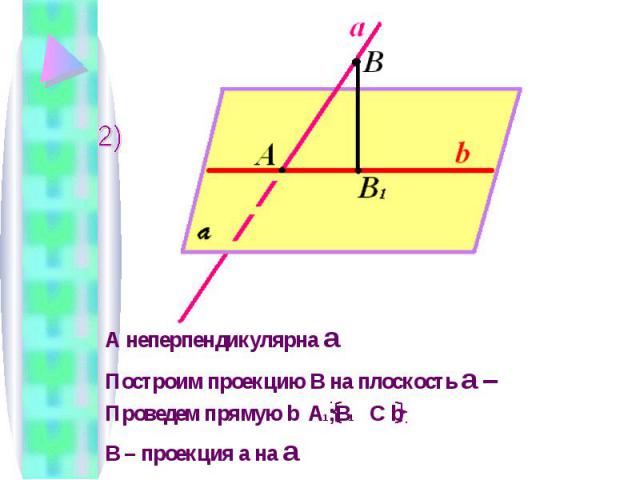
А неперпендикулярна a Построим проекцию В на плоскость a – Проведем прямую b A 1 ;B 1 C b B – проекция a на a
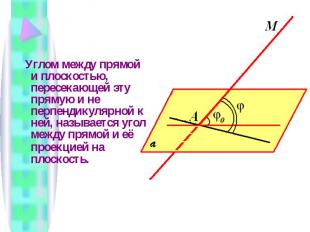
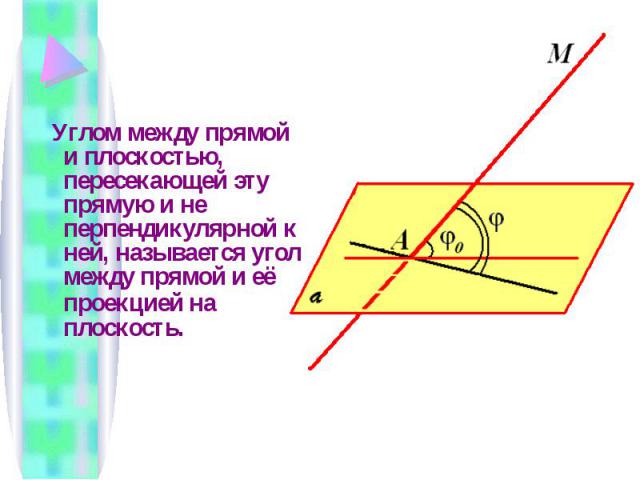
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и её проекцией на плоскость.

Презентацию выполнила Яковлева Маша, ученица 10 «А» класса Учитель Шмелёва О.В.