Презентация на тему: Перпендикулярность прямой и плоскости
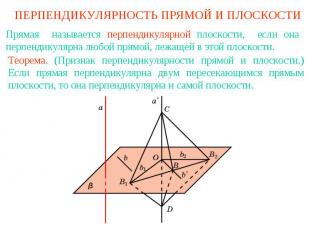
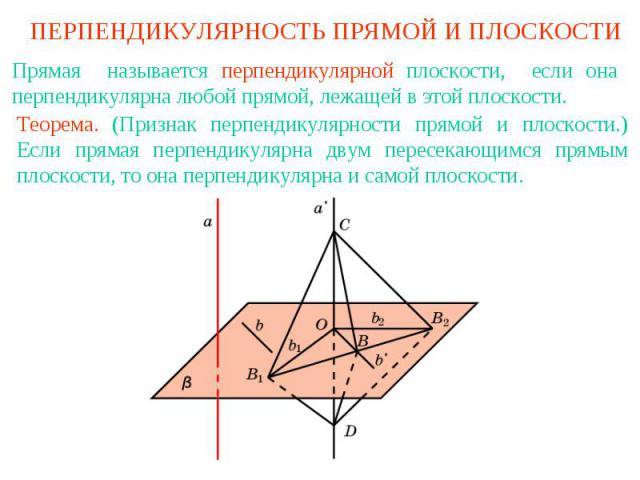
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИПрямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.Теорема. (Признак перпендикулярности прямой и плоскости.) Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна и самой плоскости.
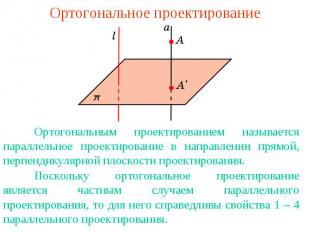
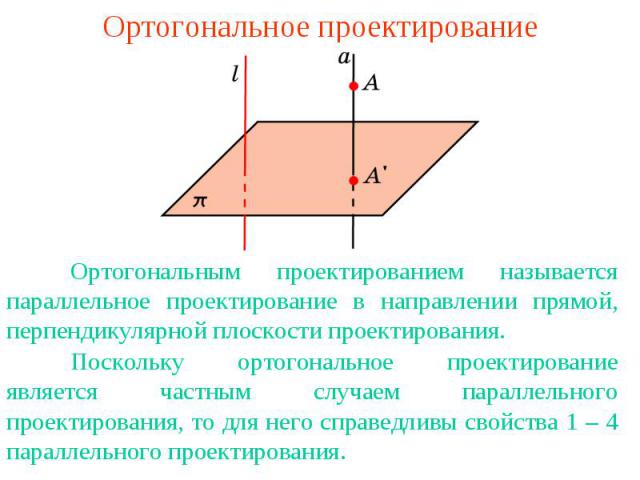
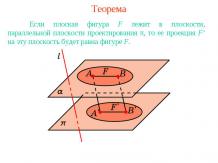
Ортогональное проектированиеОртогональным проектированием называется параллельное проектирование в направлении прямой, перпендикулярной плоскости проектирования.Поскольку ортогональное проектирование является частным случаем параллельного проектирования, то для него справедливы свойства 1 – 4 параллельного проектирования.
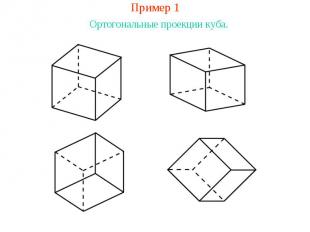
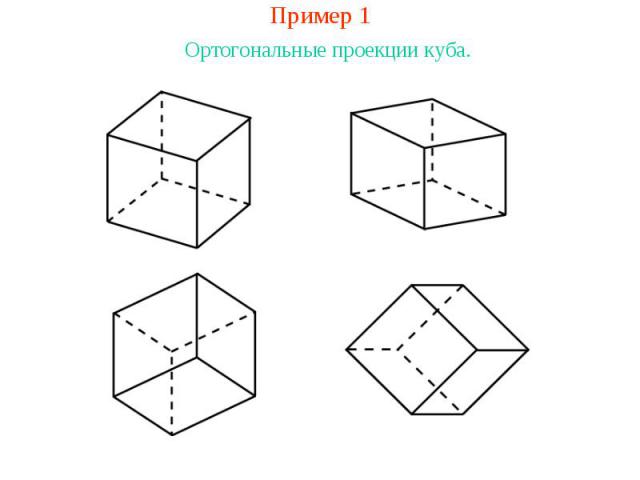
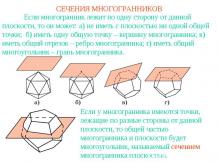
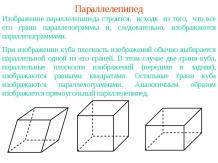
Пример 1Ортогональные проекции куба.
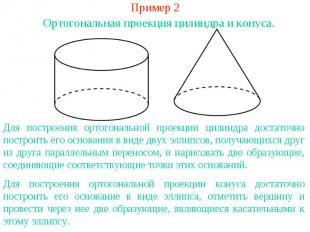
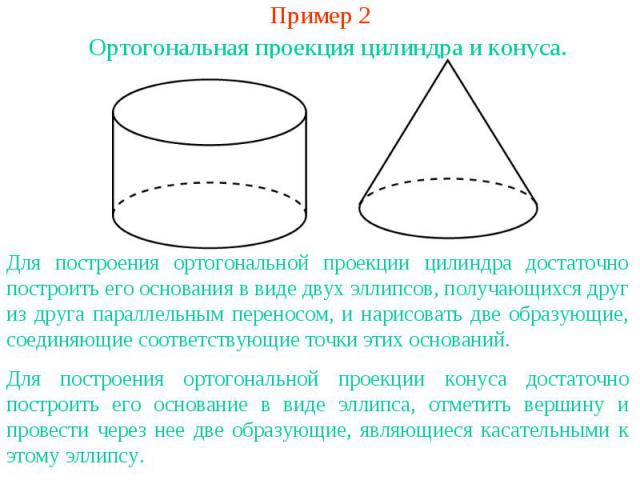
Пример 2Ортогональная проекция цилиндра и конуса.Для построения ортогональной проекции цилиндра достаточно построить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований.Для построения ортогональной проекции конуса достаточно построить его основание в виде эллипса, отметить вершину и провести через нее две образующие, являющиеся касательными к этому эллипсу.
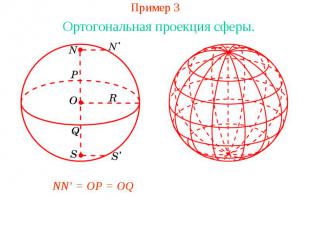
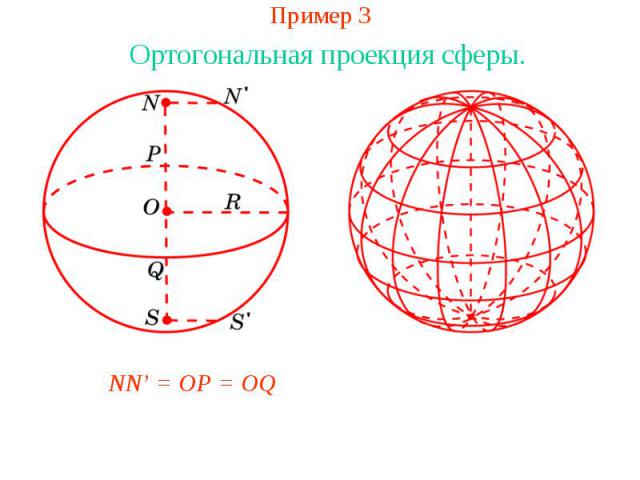
Пример 3Ортогональная проекция сферы.

Упражнение 1Верно ли, что если прямая перпендикулярна каким-нибудь двум прямым плоскости, то она перпендикулярна этой плоскости?

Упражнение 2Прямая параллельна плоскости. Может ли она быть перпендикулярной какой-нибудь прямой, лежащей в этой плоскости?

Упражнение 3Боковое ребро параллелепипеда перпендикулярно диагонали основания. Верно ли, что этот параллелепипед является прямым?

Упражнение 4Что представляет собой геометрическое место точек, расположенных на прямых, проходящих через данную точку на прямой и перпендикулярных этой прямой?

Упражнение 5Как расположена относительно плоскости треугольника прямая, перпендикулярная двум его сторонам?

Упражнение 6Найдите ГМТ в пространстве, равноудалённых от двух данных точек.Ответ: Плоскость, проходящая через середину отрезка, концами которого являются данные точки, и перпендикулярная этому отрезку.

Упражнение 7При каком взаимном расположении двух прямых через одну из них можно провести плоскость, перпендикулярную другой?

Упражнение 8Определите вид треугольника, если через одну из его сторон можно провести плоскость, перпендикулярную другой стороне.
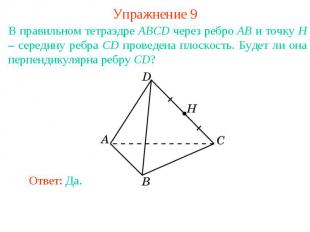
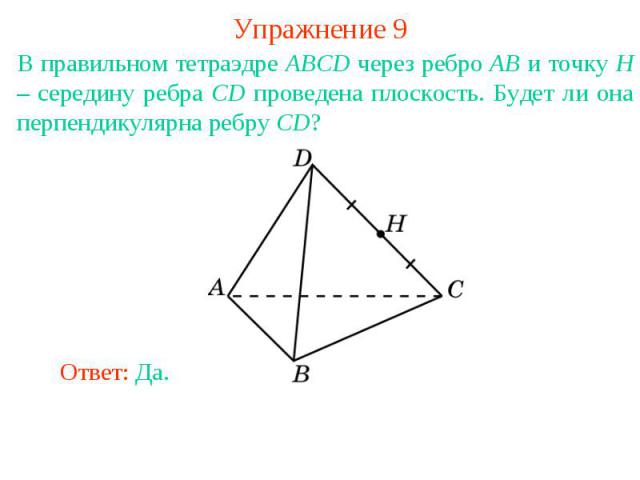
Упражнение 9В правильном тетраэдре ABCD через ребро AB и точку H – середину ребра CD проведена плоскость. Будет ли она перпендикулярна ребру CD?

Упражнение 10Найдите диагональ прямоугольного параллелепипеда, ребра которого равны a, b, c.

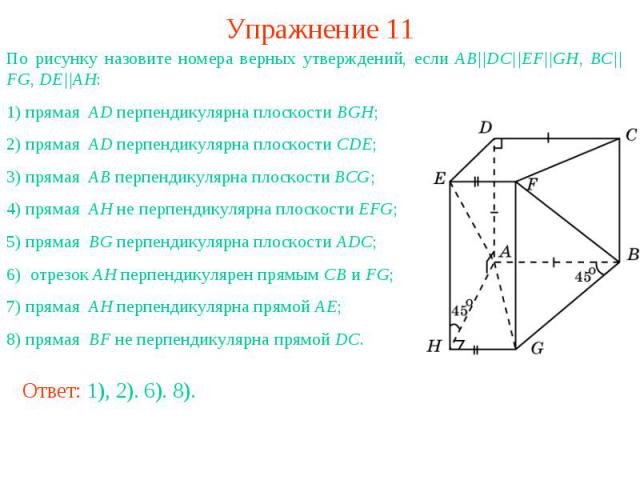
Упражнение 11По рисунку назовите номера верных утверждений, если AB||DC||EF||GH, BC||FG, DE||AH: 1) прямая AD перпендикулярна плоскости BGH;2) прямая AD перпендикулярна плоскости CDE;3) прямая AB перпендикулярна плоскости BCG;4) прямая AH не перпендикулярна плоскости EFG;5) прямая BG перпендикулярна плоскости ADC;6) отрезок AH перпендикулярен прямым CB и FG;7) прямая AH перпендикулярна прямой AE;8) прямая BF не перпендикулярна прямой DC.

Упражнение 12Может ли ортогональная проекция отрезка быть: а) меньше отрезка; б) равна отрезку; в) больше отрезка?

Упражнение 13Может ли ортогональная проекция угла быть: а) меньше угла; б) равна углу; в) больше угла?

Упражнение 14Может ли ортогональная проекция квадрата быть: а) прямоугольником; б) параллелограммом; в) трапецией?

Упражнение 15Какой фигурой является ортогональная проекция куба на плоскость, перпендикулярную диагонали куба?