Презентация на тему: Перпендикулярность прямой и плоскости

Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90°. Перпендикулярность прямых а и b обозначается так: а ⊥b. Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися. Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90°. Перпендикулярность прямых а и b обозначается так: а ⊥b. Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.

Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Теорема: Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости. Теорема: Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости. Дано: а ⊥р, а ⊥q, р и q лежат в плоскости α. р ⋂q = О. Доказать: а ┴ α Доказательство: Рассмотрим случай, когда прямая а проходит через т. О(рис. а). Проведём через т.О прямую l, параллельную прямой m . Отметим на прямой а точки А и В, чтобы АО=ОВ, и проведём в плоскости α прямую, пересекающие прямые р, q, и l соответственно в т. Р, Q, и L. Т.к. р и q – серединные перпендикуляры к отрезку АВ, то АР=ВР и АQ=ВQ. Следовательно, ΔАРQ= ΔВРQ по трём сторонам, поэтому углы АРQ и ВРQ равны ΔАРL= ΔВРL, поэтому АL=BL. Следовательно ΔАВL-равнобедренный и l ⊥а. Т.к. l ║m, l ⊥ а, то m ⊥а. Итак а ⊥ α. Рассмотрим случай, когда прямая а не проходит через т.О. Проведём через т.О прямую а, а1 ║а. По лемме а1 ⊥ р и а1 ⊥ q, поэтому а1 ⊥ α. Отсюда, а ⊥ α. Теорема доказана.

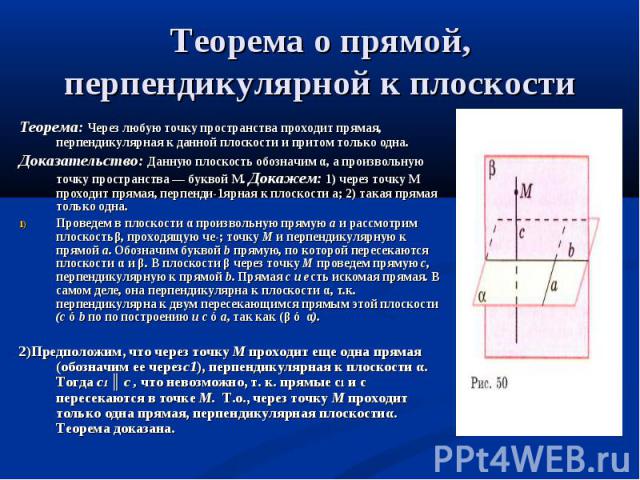
Теорема: Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости и притом только одна. Доказательство: Данную плоскость обозначим α, а произвольную точку пространства — буквой М. Докажем: 1) через точку М проходит прямая, перпенди-1ярная к плоскости а; 2) такая прямая только одна. Проведем в плоскости α произвольную прямую а и рассмотрим плоскостьβ, проходящую че-; точку М и перпендикулярную к прямой а. Обозначим буквой b прямую, по которой пересекаются плоскости α и β. В плоскости β через точку М проведем прямую с, перпендикулярную к прямой b. Прямая с и есть искомая прямая. В самом деле, она перпендикулярна к плоскости α, т.к. перпендикулярна к двум пересекающимся прямым этой плоскости (с ⊥b по по построению и с ⊥а, так как (β ⊥ α). 2)Предположим, что через точку М проходит еще одна прямая (обозначим ее черезс1), перпендикулярная к плоскости α. Тогда с1 ║ с , что невозможно, т. к. прямые с1 и с пересекаются в точке М. Т.о., через точку М проходит только одна прямая, перпендикулярная плоскостиα. Теорема доказана.

Александрова Аня 10Б Васильева Катя 10Б Васильева Надя 10Б Гаврилова Настя 10Б Егорова Люда 10Б Научный консультант : учитель математики СОШ №6 г.Чебоксары Маркова З.Г. 2008г