Презентация на тему: Четырехугольники

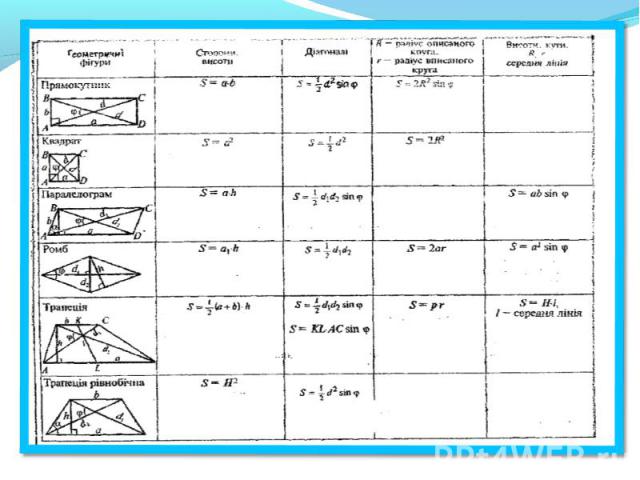
Цель: 1. Изучить признаки и свойства четырехугольников. 2. Изучить формулы. 3. Научиться решать задачи.

Историческая справка Фалес Милетский – философ, математик, астроном, основатель ионийской школы натурфилософии, купец и политический деятель. Походил из знатного финикийского рода. Фалес Милетский имеет много заслуг, в том числе и в геометрии. Считается, что Фалес первым познакомил греков с геометрией. Ему приписывают открытия и доказательства ряда теорем: о деление окружности диаметром; о том, что угол, вписанный в полукруг, является прямым; о равенстве углов при основании равнобедренного треугольника; о равенстве вертикальных углов; о пропорциональных отрезках, образованных на прямых, которые пересекаются несколькими параллельными прямыми. Фалес установил, что треугольник полностью определяется стороной и прилежащими к ней углами. Все эти достижения принесли Фалесу славу первого мудреца среди знаменитых «семи мудрецов» древности.

Четырехугольником называется фигура, состоящая и четырех точек и четырех отрезков, которые последовательно их соединяют. При этом ни одна из точек не должна лежать на одной прямой, а отрезки, которые их соединяют, не должны пересекаться. Данные точки называются вершинами четырехугольника, а отрезки, которые их соединяют, - сторонами четырехугольника. В С A, В, С, D - вершины АВ, ВС, СD, AD – стороны. А D

Четырехугольник обозначается его вершинами. Вершины четырехугольника называются соседними, если они являются концами одной из его сторон. Несоседние вершины называются противолежащими. Четырехугольник обозначается его вершинами. Вершины четырехугольника называются соседними, если они являются концами одной из его сторон. Несоседние вершины называются противолежащими. Отрезки, которые соединяют противолежащие вершины четырехугольника, называются диагоналями. Стороны четырехугольника, которые выходят из его вершины, называются соседними. Стороны, которые не имеют общих вершин, называются противолежащими. Сумма длин всех сторон четырехугольника называется периметром. АВСD - четырехугольник А и В – соседние; А и С – противолежащие В С АС и ВD – диагонали ВС и СD – соседние ВС и АD – противолежащие Р = АВ+ВС+СD+AD А D

Параллелограмм – это четырехугольник, у которого противолежащие стороны попарно параллельны. Параллелограмм – это четырехугольник, у которого противолежащие стороны попарно параллельны. В С АВСD - параллелограмм АВ СD, ВС АD А D

Прямоугольник – это параллелограмм, у которого все углы прямые. Прямоугольник – это параллелограмм, у которого все углы прямые. В С АВСD - параллелограмм АВ СD, ВС АD А D

Ромб – это параллелограмм, у которого все стороны равны. Ромб – это параллелограмм, у которого все стороны равны. В АВСD - ромб А С АВ=ВС=CD=AD D

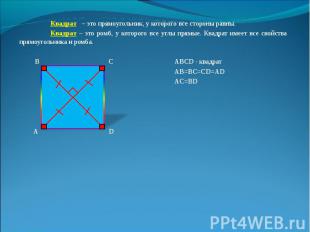
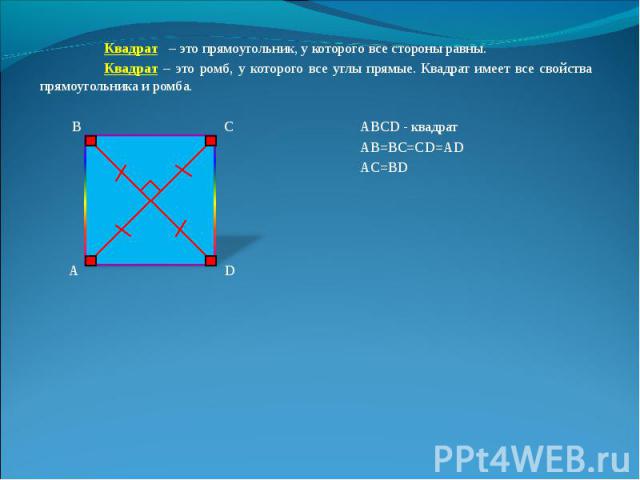
Квадрат – это прямоугольник, у которого все стороны равны. Квадрат – это прямоугольник, у которого все стороны равны. Квадрат – это ромб, у которого все углы прямые. Квадрат имеет все свойства прямоугольника и ромба. В С ABCD - квадрат АВ=ВС=СD=AD AC=BD А D

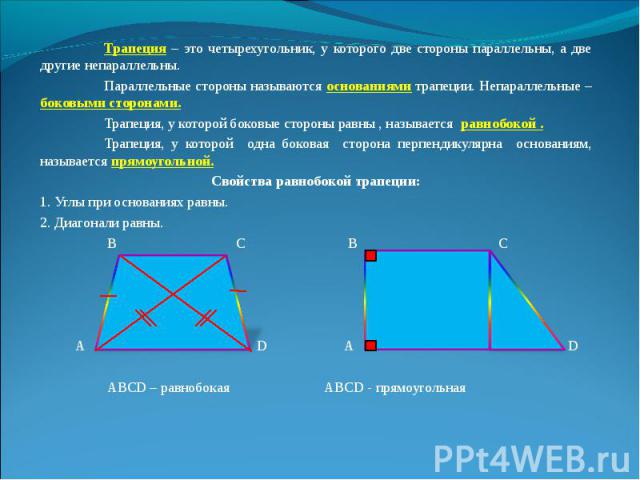
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие непараллельны. Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие непараллельны. Параллельные стороны называются основаниями трапеции. Непараллельные – боковыми сторонами. Трапеция, у которой боковые стороны равны , называется равнобокой . Трапеция, у которой одна боковая сторона перпендикулярна основаниям, называется прямоугольной. Свойства равнобокой трапеции: 1. Углы при основаниях равны. 2. Диагонали равны. В С В С A D A D АВСD – равнобокая АВСD - прямоугольная

ТЕСТЫ ТЕСТЫ 1. Одна из сторон параллелограмма в 4 раза больше другой, а его периметр равен 30см. Чему равны стороны параллелограмма? 1) 4см, 16см, 4см, 16см; 2) 6см, 24см, 6см, 24см; 3) 3см, 12см, 3см, 12см. 2. Одна из сторон прямоугольника вдвое меньше другой стороны. Зная, что периметр равен 42см, найдите длины сторон. 1) 6см, 12см; 2) 7см, 14см; 3) 8см, 16см. 3. Найдите периметр ромба АВСD зная, что длина его меньшей диагонали АС=4см, тупой угол равен 120°. 1) 64см; 2) 20см; 3) 6см. 4. Периметр параллелограмма равен 28см. Одна из сторон равна 8см. Найдите меньшую сторону параллелограмма . 1) 7см; 2) 6см; 3) 5см; 4) ваш ответ.

5. Боковая сторона равнобедренной трапеции равна 8см. Средняя линия равна 10см. Найдите периметр данной трапеции. 5. Боковая сторона равнобедренной трапеции равна 8см. Средняя линия равна 10см. Найдите периметр данной трапеции. 1)20см; 2) 16см; 3) 18см; 4) 36см. 6. В параллелограмме сторона АВ равна 6см, диагонали равны 9см и 5см, О – точка пересечения диагоналей. Чему равен периметр треугольника АОВ? 1) 13см; 2) 12см; 3) 14см. 7. Биссектрисы углов прямоугольника пересекаются в точках М, N, Р, К. Какого вида четырехугольник с вершинами в этих точках? 1) ромб; 2) прямоугольник; 3) квадрат. 8. Средняя линия трапеции равна 10см, а одно из его оснований – 4см. Найдите второе основание трапеции. 1) 8см; 2) 12см; 3) 16см.

9. Диагональ параллелограмма образует с двумя его сторонами углы 30 и 5о . Вычислите углы параллелограмма. 9. Диагональ параллелограмма образует с двумя его сторонами углы 30 и 5о . Вычислите углы параллелограмма. 1) 50°, 130°; 2) 120°, 60°; 3) 80°, 100°. 10. Длины оснований трапеции относятся, как 4 : 7, длина средней линии 33см. Найдите длины оснований трапеции. 1) 12см, 21см; 2) 24см, 42см; 3) 16см, 28см. 11. Диагонали ромба равны 8см и 6см. Найдите периметр ромба. 1) 40см; 2) 20см; 3) 24см. 12. Найдите по рис. углы между диагоналями прямоугольника. В С А D 1) 90° и 90°; 2) 140° и 40°; 3) 40° и 160°.°

13. Найдите диагональ прямоугольника, если одна из его сторон 8см, а периметр раве46. 13. Найдите диагональ прямоугольника, если одна из его сторон 8см, а периметр раве46. 1) 17см; 2) 23см; 3) 20см. 14. Найдите периметр прямоугольника, если одна его сторона 5см, а диагональ 13см. 1) 17см; 2) 26см; 3) 34см. 15. Дан квадрат АВСD со стороной 4см. На стороне CD взята точка Е, такая, что ЕА = 5см. Найдите СЕ. 1) 1см; 2) 14см; 3) 12см. 16. В трапеции АВСD (AD и ВС основания) А = 90°, С = 135°, АВ=ВС=2см. Найдите среднюю линию трапеции. 1) 3см; 2) 2,5см; 3) 4см.

17. Угол между диагоналями прямоугольника равен 60 , а меньшая сторона равна 4см. 17. Угол между диагоналями прямоугольника равен 60 , а меньшая сторона равна 4см. Найдите диагональ. 1) 2см; 2) 10см; 3) 8см. 18. Большая диагональ параллелограмма делит его углы на части, градусная, мера которых 30° и 50° . Найдите углы параллелограмма. 1) 80°, 100°, 80°, 100°; 2) 50°, 130°, 50°, 130°; 3) 30°, 150°, 30°, 150°. 19. В равнобокой трапеции МНКР проведен перпендикуляр НЕ к большему основанию МР, МЕ = 6см, НК = 10см. Найдите большее основание и среднюю линию трапеции. 1) 32см, 22см; 2) 22см, 16см; 3) 16см, 32см. 20. В прямоугольной трапеции АВСD, АD ВC. Из вершины В на сторону АD опущен перпендикуляр ВК. Найдите ВК, если АВ = 6см и АВК = 30°. 1) 3см; 2) 10см; 3) .

ОТВЕТЫ ОТВЕТЫ 3 11. 2 2 12. 2 3 13 . 1 2 14. 3 4 15. 1 1 16. 1 1 17. 3 3 18. 1 3 19. 2 2 20. 1

Вывод: В процессе работы мы познакомились с открытиями и доказательствами теорем великого математика Фалеса, изучили признаки и свойства четырехугольников, изучили формулы, а также научились решать задачи.